G.Finding the Radius for an Inserted Circle 2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

地址：https://nanti.jisuanke.com/t/17314

题目：

Three circles C_{a}Ca, C_{b}Cb, and C_{c}Cc, all with radius RR and tangent to each other, are located in two-dimensional space as shown in Figure 11. A smaller circle C_{1}C1 with radius R_{1}R1 (R_{1}<RR1<R) is then inserted into the blank area bounded by C_{a}Ca, C_{b}Cb, and C_{c}Cc so that C_{1}C1 is tangent to the three outer circles, C_{a}Ca, C_{b}Cb, and C_{c}Cc. Now, we keep inserting a number of smaller and smaller circles C_{k}\ (2 \leq k \leq N)Ck (2≤k≤N) with the corresponding radius R_{k}Rk into the blank area bounded by C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1 (2 \leq k \leq N)(2≤k≤N), so that every time when the insertion occurs, the inserted circle C_{k}Ck is always tangent to the three outer circles C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1, as shown in Figure 11

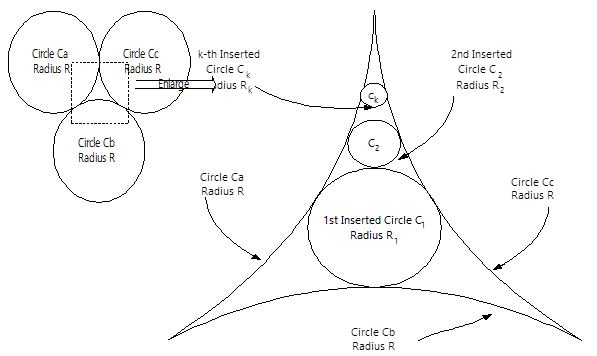
Figure 1.

(Left) Inserting a smaller circle C_{1}C1 into a blank area bounded by the circle C_{a}Ca, C_{b}Cb and C_{c}Cc.

(Right) An enlarged view of inserting a smaller and smaller circle C_{k}Ck into a blank area bounded by C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1 (2 \leq k \leq N2≤k≤N), so that the inserted circle C_{k}Ck is always tangent to the three outer circles, C_{a}Ca, C_{c}Cc, and C_{k-1}Ck−1.

Now, given the parameters RR and kk, please write a program to calculate the value of R_{k}Rk, i.e., the radius of the k-thk−th inserted circle. Please note that since the value of R_kRk may not be an integer, you only need to report the integer part of R_{k}Rk. For example, if you find that R_{k}Rk = 1259.89981259.8998 for some kk, then the answer you should report is 12591259.

Another example, if R_{k}Rk = 39.102939.1029 for some kk, then the answer you should report is 3939.

Assume that the total number of the inserted circles is no more than 1010, i.e., N \leq 10N≤10. Furthermore, you may assume \pi = 3.14159π=3.14159. The range of each parameter is as below:

1 \leq k \leq N1≤k≤N, and 10^{4} \leq R \leq 10^{7}104≤R≤107.

Input Format

Contains l + 3l+3 lines.

Line 11: ll ----------------- the number of test cases, ll is an integer.

Line 22: RR ---------------- RR is a an integer followed by a decimal point,then followed by a digit.

Line 33: kk ---------------- test case #11, kk is an integer.

\ldots…

Line i+2i+2: kk ----------------- test case # ii.

\ldots…

Line l +2l+2: kk ------------ test case #ll.

Line l + 3l+3: -1−1 ---------- a constant -1−1 representing the end of the input file.

Output Format

Contains ll lines.

Line 11: kk R_{k}Rk ----------------output for the value of kk and R_{k}Rk at the test case #11, each of which should be separated by a blank.

\ldots…

Line ii: kk R_{k}Rk ----------------output for kk and the value of R_{k}Rk at the test case # ii, each of which should be separated by a blank.

Line ll: kk R_{k}Rk ----------------output for kk and the value ofR_{k}Rk at the test case # ll, each of which should be separated by a blank.

样例输入

样例输出

1 23665

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

思路：

　　圆的反演。

　　很容易想到把上面两大圆的切点作为反演中心，这样会得到下图。

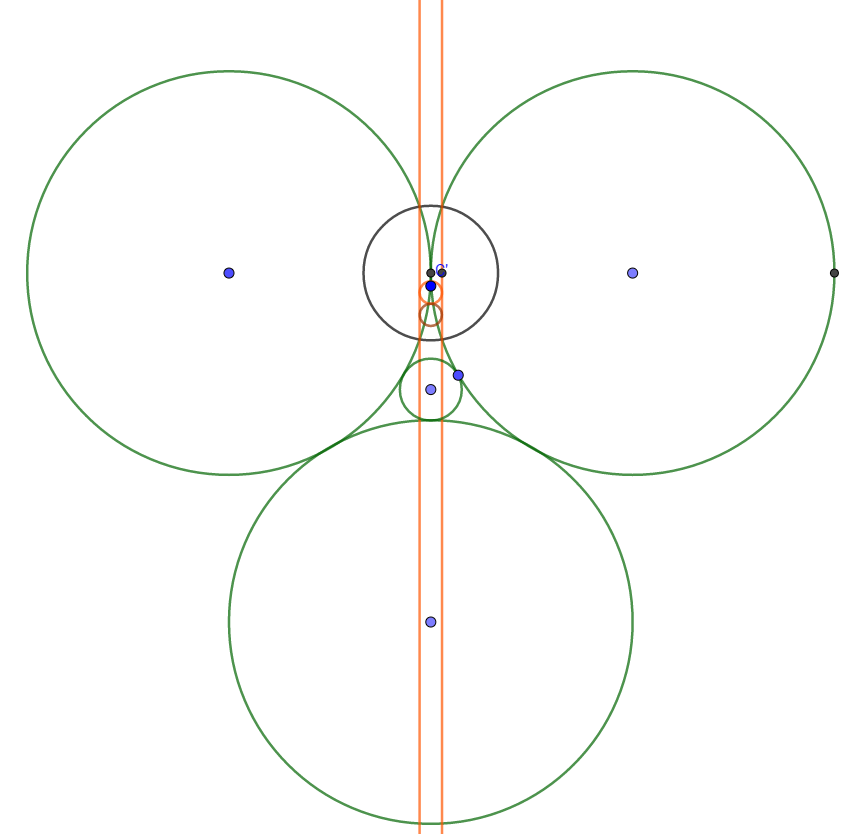
　　绿色的是反演前的圆，黄色的是反演后的图形，两个大圆成了平行直线，下面的大圆成了直线间的小圆，后面添加的圆都在这个小圆的下面。

　　所以求出小圆的圆心的y即可，然后反演回去可以得到半径。

 #include <bits/stdc++.h>

 using namespace std;

 #define MP make_pair

 #define PB push_back

 typedef long long LL;

 typedef pair<int,int> PII;

 const double eps=1e-;

 const double PI=acos(-1.0);

 const int K=1e6+;

 const int mod=1e9+;

 int main(void)

 {

     double r,x,y,ls,dis,ans[];

     int t;

     cin>>t>>r;

     x=0.5*r,ls=-0.5*sqrt(3.0)*r;

     dis=x*x+ls*ls;

     ls=ls/dis;

     r=1.0/(*r);

     for(int i=;i<=;i++)

     {

         y=ls-r*;

         ans[i]=0.5*(1.0/(y-r)-1.0/(y+r));

         ls=y;

     }

     for(int i=,k;i<=t;i++)

         scanf("%d",&k),printf("%d %d\n",k,(int)ans[k]);

     return ;

 }