关于区间DP的一点点心得（虽然还是很菜）

自己今天对于区间 DP 的一个总结

1. 区间 DP 的数组一般是二维，其状态一般表示区间 \((l,r)\)。

2. 区间 DP 在思考的时候是有一定套路的，思考时可以按照如下方式进行思考：

   1. 这段区间要维护的信息是什么（即 \(dp\) 或 \(f\) 数组内的值应该存什么）？
   2. 状态的边界如何设计（这个我认为对于所有的 DP 来说，都应当是其思考过程之一）？
   3. 这段区间如何从它的更小的区间推广过来（即如何从 \(dp(l,r)\) 或 \(f(l,r)\) 的子区间转移到本身）？
   4. 怎样合并或更新信息（即如何统计信息或如何设计状态转移方程，是取最大值还是最小值，是应该使用加法原理合并方案数还是用乘法原理）？

   对于大部分人（尤其是我）来说，以上四点基本上是区间 DP 的全部思维难点。

   对于第一条来说，如果让我们维护最大值，我们应当怎么办，维护方案个数我们又应当怎么设计维护的信息。

   对于第二条来讲，我们应当考虑一下数组的初始值应当是什么值，边界值又应当是什么值，那些情况下就到达了边界情况等等都应当被考虑，并且编写代码的时候千万不要忘了这一步，否则很有可能会莫名其妙地 WA 掉。

   而对于第三条如何推广，是通过两个子区间推广过来（即为 \(dp(l,r)\) 是从 \(dp(l,k)\) 和 \(dp(k+1,r)\) 转移而来），还是单纯的左端点减一或右端点减一推广而来（例如题目 P3205 [HNOI2010]合唱队）。

   至于第四条，就是要考虑合并子区间信息并更新区间信息时，我们如何正确的合并（例如单纯的加减），并且如何正确的更新区间信息（例如单纯的赋值），还有就是需不需要进行分类讨论，有没有什么可能会出现的坑点之类。

3. 区间 DP 的板子：
   
   众所周知，DP 类题目一般是没有板子的，但是根据自己那微薄的做题量分析，发现其中还是有一定的规律的，基本形式如下：

memset(dp,状态初始值,sizeof(dp));
for(int i=1;i<=n;i++)
	dp[i][i] = 状态边界值;
for(int len = 2;len<=n;++len){
	for(int l=1;l+len-1<=n;++l){
		int r = l+len-1;
		//这里写如何从子区间当中推广出来
	}
}
cout<<dp[1][n]<<endl;//统计答案并输出（注意，这里所写的方法不唯一，在某些情况下不适用！！）

1. 例题：

   1. P1775 石子合并（弱化版）：
      
      区间 DP 的板子题，不像他的标配版那样还需要断环成链。
      
      这道题的思考过程如下：

      1. 这段区间我们需要维护的是这段区间内可行的最小代价。
      2. 状态边界应该是 \(\forall i \in [1,n] dp(i,i) = 0\)，其他地方设为 \(\infty\)。原因非常简单，因为我们在没有合并的时候（也就是最初始的每一堆），我们没有任何代价的产生，故 \(dp(i,i)\) 应该设为 \(0\)。
      3. 大区间应当是把其自己分成两个小区间，从而推广而来，因为我们每次合并都是合并两堆。
      4. 大区间的值（状态转移方程）应当是 \(dp(l,r) = \min_{\,l\le k\le r}\{dp(l,k)+dp(k+1,r)\}\)，原因是根据第三条，我们需要把大区间分成待合并的两个小区间，那么此时两个合成小区间的代价加上本次合成成本区间的代价才是最终的代价，因为合成本区间的代价是固定的，所以本区间的代价的最小值应当为两个小区间的代价的和的最小值，故大区间的值（状态转移方程）为：\(dp(l,r) = \min_{\,l\le k\le r}\{dp(l,k)+dp(k+1,r)\}\)。
         
         代码如下：

      #include <bits/stdc++.h>
      using namespace std;
      #define MAX_SIZE (int)8e2
      int dpmin[MAX_SIZE][MAX_SIZE];
      int a[MAX_SIZE];
      int sum[MAX_SIZE];
      int main(){
      	int n;
      	cin>>n;
      	for(int i=1;i<=n;i++)
      		cin>>a[i];
      	memset(dpmin,0x3f,sizeof(dpmin));
      	for(int i=1;i<=2*n;i++){
      		dpmin[i][i] = 0;
      		sum[i] = sum[i-1] + a[i];
      	}
      	for(int len=2;len<=n;len++){
      		for(int l=1;l<n;l++){
      			int r = l+len-1;
      			for(int k=l;k<r;k++){
      				dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]+dpmin[k+1][r]);
      			}
      			dpmin[l][r] += sum[r]-sum[l-1];
      		}
      	}
      	cout<<dpmin[1][n]<<endl;
      	return 0;
      }
      

   2. P1880 [NOI1995] 石子合并：
      
      这道题和弱化版的思路是一样的，只是多了一个断环成链的小 trick，下面我们来浅浅的说一下怎么断环成链和为什么这样做的正确的。

      1. 首先我们有一个环（这里以长度为 8 举例，如下图）：
         
         
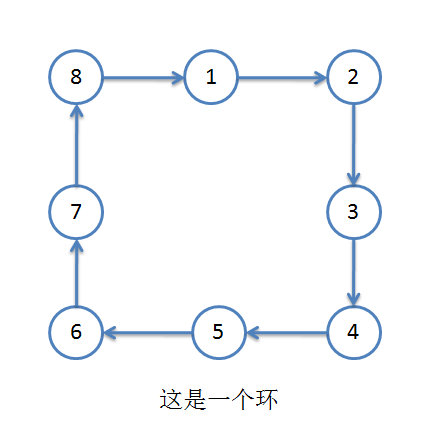
      2. 然后我们我们把它 copy 一倍，挂在后面（如下图）：
         
         
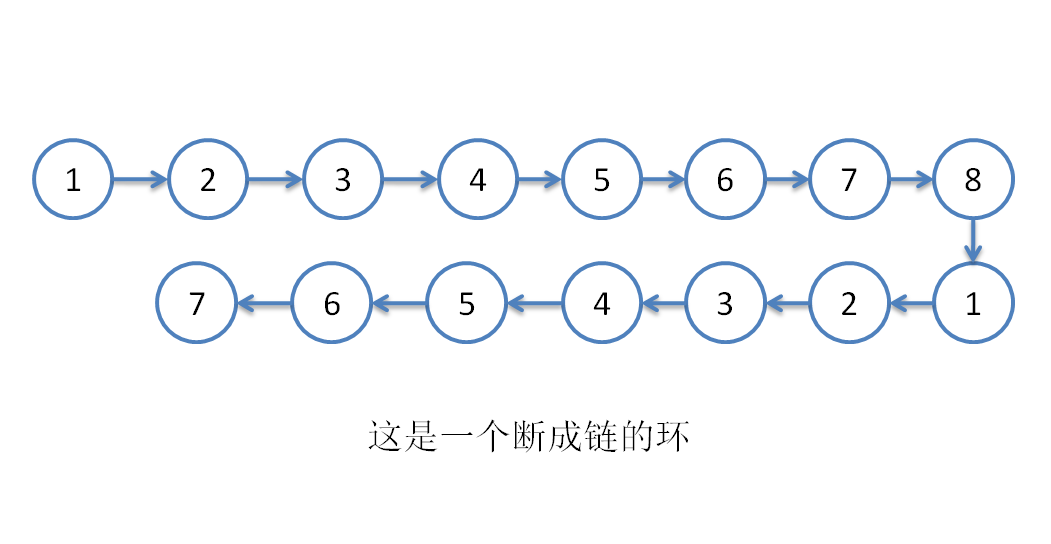
      3. 我们可以简单看一下，如果我们想从 2 号节点来遍历环的话，对于断链之前，它是这样的：
         
         
         
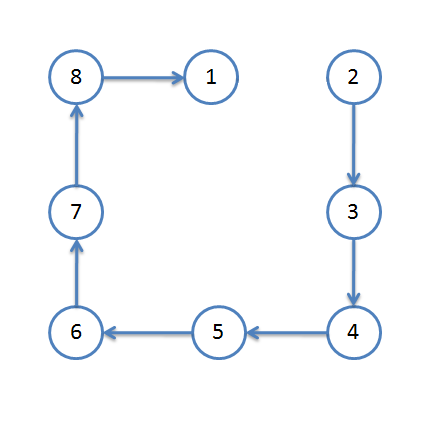
         断链之后，他是这样的（蓝色部分为得到的结果）：
         
         
         
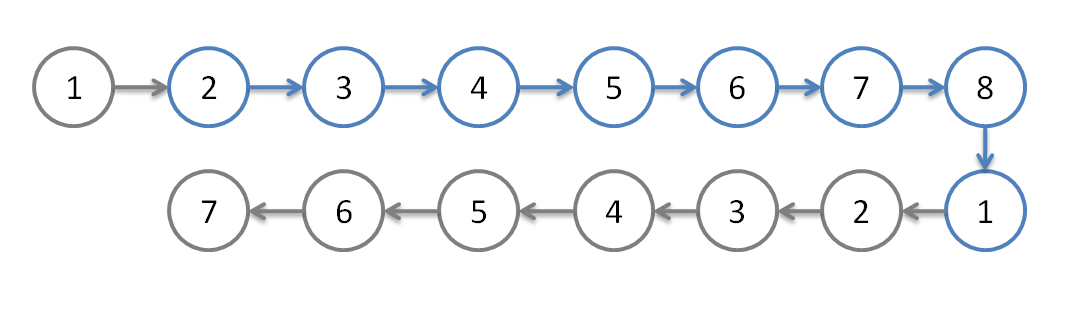
         可以看出，通过这种方式断环成链，实际访问到的结果和真实的结果是一样的，但这样有一个好处，就是它把一个具有后效性的环变成了没有后效性的链，致使其可以 DP。
         
         代码如下：

      #include <bits/stdc++.h>
      using namespace std;
      #define MAX_SIZE (int)3e2
      int dpmin[MAX_SIZE][MAX_SIZE];
      int dpmax[MAX_SIZE][MAX_SIZE];
      int a[MAX_SIZE];
      int sum[MAX_SIZE];
      int main(){
      	int n;
      	cin>>n;
      	for(int i=1;i<=n;i++)
      		cin>>a[i];
      	for(int i=n+1;i<=2*n;i++)
      		a[i] = a[i-n];
      	memset(dpmin,0x3f,sizeof(dpmin));
      	memset(dpmax,0xff,sizeof(dpmax));
      	for(int i=1;i<=2*n;i++){
      		dpmin[i][i] = 0;
      		dpmax[i][i] = 0;
      		sum[i] = sum[i-1] + a[i];
      	}
      	for(int len=2;len<=n;len++){
      		for(int l=1,r=l+len-1;(l<2*n)&&(r<2*n);l++,r=l+len-1){
      			for(int k=l;k<r;k++){
      				dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]+dpmin[k+1][r]);
      				dpmax[l][r] = max(dpmax[l][r],dpmax[l][k]+dpmax[k+1][r]);
      			}
      			dpmin[l][r] += sum[r] - sum[l-1];
      			dpmax[l][r] += sum[r] - sum[l-1];
      		}
      	}
      	int minans = INT_MAX;
      	int maxans = INT_MIN;
      	for(int i=1;i<=n;i++){
      		minans = min(minans,dpmin[i][i+n-1]);
      		maxans = max(maxans,dpmax[i][i+n-1]);
      	}
      	cout<<minans<<endl;
      	cout<<maxans<<endl;
      	return 0;
      }
      

   3. P1063 [NOIP2006 提高组] 能量项链：
      
      有点水，就是石子合并（弱化版）的一个变种，区别在于我们合并信息时从两个子区间的和加区间和变成了加左端点、右端点和子区间断点的乘积，即把方程变成：\(dp(l,r) = \max_{k\in [l,r)} \{dp(l,r),dp(l,k)+dp(k+1,r)+a_i\times a_{k+1} \times a_{r+1}\}\)
      
      代码如下：

   #include <bits/stdc++.h>
   using namespace std;
   #define MAX_SIZE (int)400
   int a[MAX_SIZE];
   int dp[MAX_SIZE][MAX_SIZE];
   int n;
   int main(){
       cin>>n;
       for(int i=1;i<=n;i++)
           cin>>a[i];
       for(int i=n+1;i<=2*n+1;i++)
           a[i] = a[i-n];
       memset(dp,0xcf,sizeof(dp));
       for(int i=1;i<2*n;i++)
           dp[i][i] = 0;
       for(int len=2;len<=n;len++){
           for(int l=1,r=l+len-1;l<=2*n&&r<=2*n;++l,r=l+len-1){
               for(int k=l;k<r;k++)
                   dp[l][r] = max(dp[l][r],dp[l][k]+dp[k+1][r]+a[l]*a[k+1]*a[r+1]);
           }
       }
       int maxans = INT_MIN;
       for(int i=1;i<=n;i++)
           maxans = max(maxans,dp[i][i+n-1]);
       cout<<maxans<<endl;
       return 0;
   }
   

   1. P3146 [USACO16OPEN]248 G:
      
      是一道很不错的石子合并类问题的变种，刚开始没有明白思路，因为不知道怎么达成游戏中 “合并” 的操作，于是大概想了有 1 个小时，然后意识到合并是针对于两个块块来说的。
      
      这下思路就很简单了，我们可以用 \(dp(l,r)\) 表示若从 \(l\) 到 \(r\) 能合并，则代表合并后的值，否则为 0 或 \(-\infty\)（这里为什么为 0 或 \(-\infty\) 呢，因为虽然不能合并，但是却不影响我们的子区间的答案，或者也可以理解这个区间因为不能合并，所以他不存在，那么不存在的话如何让其不影响我们的答案呢，因为要统计最大值且保证答案属于 \(\mathbb{N_+}\)，所以我们直接使用 0 或 \(-\infty\) 来填充这一块，表示我这一个块块不存在）。
      
      故可以列出其状态转移方程，如下：
      • 若子区间存在，且能合并，则：\(dp(l,r) = \max_{k \in (l,r)}\{\,dp(l,r),\;dp(l,k+1)\,\}\)
      • 否则：\(dp(l,r) = 0\)
        
        代码如下：

   #include <bits/stdc++.h>
   using namespace std;
   #define MAX_SIZE (int)300
   int n;
   int a[MAX_SIZE];
   int dp[MAX_SIZE][MAX_SIZE];
   int main(){
       cin>>n;
       for(int i=1;i<=n;i++)
           cin>>a[i];
       memset(dp,0,sizeof(dp));
       for(int i=1;i<=n;i++)
           dp[i][i] = a[i];
       for(int len=2;len<=n;len++){
           for(int l=1;l<=n-len+1;l++){
               int r = l+len-1;
               for(int k=l;k<r;k++){
                   if(dp[l][k]==dp[k+1][r]&&dp[l][k])
                       dp[l][r] = max(dp[l][r],dp[l][k]+1);
               }
           }
       }
       int maxnum = -1;
       for(int i=1;i<=n;i++)
           for(int j=1;j<=n;j++)
               maxnum = max(maxnum,dp[i][j]);
       cout<<maxnum;
       return 0;
   }
   

   1. P4342 [IOI1998]Polygon:
      
      感觉难度有点虚标，这道题的思考时间比上一题短得多，大概也就 25 min 左右。
      
      实际上核心思考还是石子合并（需要断环成链），就是因为乘法和负整数的存在，我们需要进行一个小小的分类讨论：
      
      首先，我们要明确一个问题，两个负整数相乘不一定比两个正整数大，因为有负负得正这一规则存在，但是，不论是两个负整数相加还是一个正整数加上一个负整数，都一定比两个正整数相加小，根据这一点性质，我们需要多维护一个最小值，并且对上述性质进行讨论。
      1. 如果操作是相加，那么正常合并，即为:
         • \(dpmax(l,r)=\max_{k\in[l,r)}\{dpmax(l,r),dpmax(l,k)+dpmax(k+1,r)\}\)
         • \(dpmin(l,r) = \min_{k\in[l,r)}\{dpmin(l,r),dpmin(l,k)+dpmin(k+1,r)\}\)
      2. 如果是相乘，我们就需要分类讨论，即：
         • \(dpmax(l,r) = \max_{k\in[l,r)}\{dpmax(l,r),\max\{dpmax(l,k)*dpmax(k+1,r),dpmin(l,k)*dpmin(k+1,r)\}\}\)
         • \(dpmin(l,r) = \min_{k\in[l,r)}\{dpmin(l,r),\min\{\min\{dpmin(l,k)*dpmin(k+1,r),dpmin(l,k)*dpmax(k+1,r)\},dpmax(l,k)*dpmin(k+1,r)\}\}\)
           
           代码如下：

   #include <bits/stdc++.h>
   using namespace std;
   #define MAX_SIZE (int)200
   long long dpmax[MAX_SIZE][MAX_SIZE];
   long long dpmin[MAX_SIZE][MAX_SIZE];
   char edge[MAX_SIZE];
   int ver[MAX_SIZE];
   int main(){
       int n;
       cin>>n;
       for(int i=1;i<=n;++i)
           cin>>edge[i]>>ver[i];
       for(int i=n+1;i<=2*n;++i){
           edge[i] = edge[i-n];
           ver[i] = ver[i-n];
       }
       for(int i=0;i<MAX_SIZE;++i)
           for(int j=0;j<MAX_SIZE;++j){
               dpmax[i][j] = LONG_LONG_MIN;
               dpmin[i][j] = LONG_LONG_MAX;
           }
       for(int i=1;i<=2*n;++i){
           dpmax[i][i] = ver[i];
           dpmin[i][i] = ver[i];
       }
       for(int len=2;len<=n;++len){
           for(int l=1,r=l+len-1;(l<2*n)&&(r<2*n);++l,r=l+len-1){
               for(int k=l;k<r;++k){
                   switch(edge[k+1]){
                       case 't':{
                           dpmax[l][r] = max(dpmax[l][r],dpmax[l][k]+dpmax[k+1][r]);
                           dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]+dpmin[k+1][r]);
                           break;
                       }
                       case 'x':{
                           dpmax[l][r] = max(dpmax[l][r],max(dpmax[l][k]*dpmax[k+1][r],dpmin[l][k]*dpmin[k+1][r]));
                           dpmin[l][r] = min(dpmin[l][r],min(dpmin[l][k]*dpmin[k+1][r],min(dpmin[l][k]*dpmax[k+1][r],dpmax[l][k]*dpmin[k+1][r])));
                           break;
                       }
                   }
               }
           }
       }
       long long maxans = LONG_LONG_MIN;
       for(int i=1;i<=n;i++){
           maxans = max(maxans,dpmax[i][i+n-1]);
       }
       cout<<maxans<<endl;
       for(int i=1;i<=n;i++){
           if(dpmax[i][i+n-1]==maxans)
               cout<<i<<' ';
       }
       return 0;
   }
   

   1. P3205 [HNOI2010]合唱队:
      
      这道题是一道经典的统计方案数题目。但是如何统计方案是一个问题，如何转移也是一个问题。
      
      我们可以给 \(dp\) 数组增加一个维度，来表示这一次插入的时候是怎么插的，0 表示从左边插入，1 表示从右边插入，然后进行一个小小的分类讨论就可以了。
      
      代码如下：

   #include <bits/stdc++.h>
   using namespace std;
   #define MAX_SIZE (int)1005
   #define MOD 19650827
   int n;
   int fin[MAX_SIZE];
   int dp[MAX_SIZE][MAX_SIZE][2];
   int main(){
       ios::sync_with_stdio(false);
       cin>>n;
       for(int i=1;i<=n;i++)
           cin>>fin[i];
       memset(dp,0,sizeof(dp));
       for(int i=1;i<=n;i++)
           dp[i][i][0] = 1;
       for(int len=2;len<=n;len++){
           for(int l=1;l<=n-len+1;l++){
               int r = l+len-1;
               if(fin[l]<fin[r])
                   dp[l][r][1] += dp[l][r-1][0];
               if(fin[l+1]>fin[l])
                   dp[l][r][0] += dp[l+1][r][0];
               if(fin[l]<fin[r])
                   dp[l][r][0] += dp[l+1][r][1];
               if(fin[r]>fin[r-1])
                   dp[l][r][1] += dp[l][r-1][1];
               dp[l][r][0] %= MOD;
               dp[l][r][1] %= MOD;
           }
       }
       cout<<(dp[1][n][0]+dp[1][n][1])%MOD;
       return 0;
   }