LeetCode 1388. Pizza With 3n Slices(3n 块披萨)(DP)

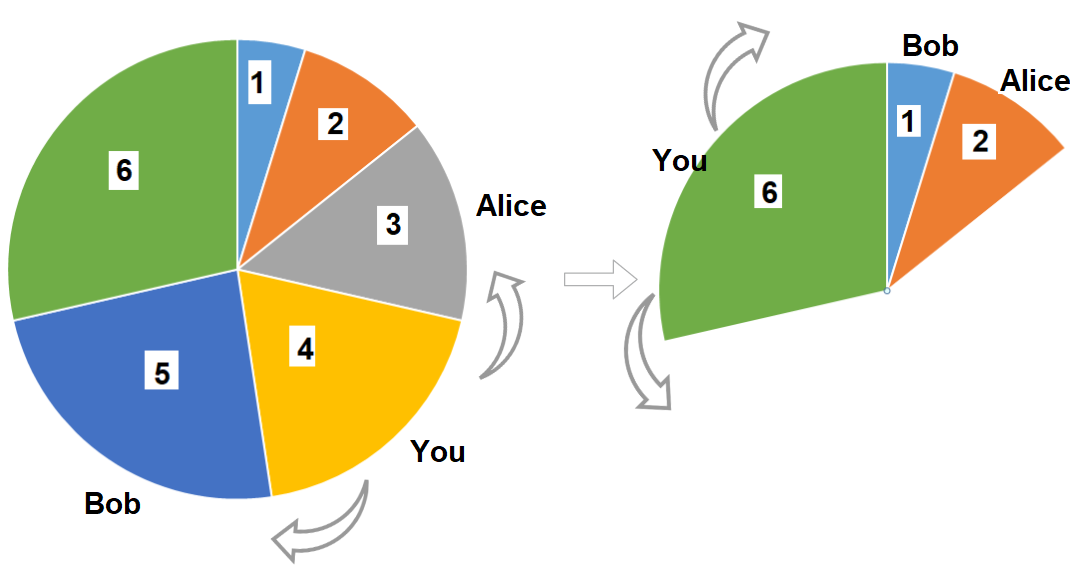
给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

你挑选 任意 一块披萨。
Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

示例 1：

输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

这条比较难的一点是论证：

题目可以转换为，取任意 n/3 个不相邻的数字的最大和。

1、首先显然相邻的两个数字是不可能同时取到的。

2、任意长度为 n/3 的不相邻的子序列都可以被取到。

　　尝试简单论证一下，

　　用0表示不选择，1表示选择，当选择不相邻的n/3个数字之后，001001001 这样的序列可以表示为一种选取方法。

　　显然，存在某个1的周围有至少三个0，如 0010 或 0100 （由于是一个圆 首尾时相连接的）

　　因为如果不存在的话，则序列只能为 010101... 显然 1 的个数会大于 n/3

　　然后先选取这样的 1 和周围的两个 0 ，那么，剩下还是会有一个 0，（不会出现两个1相邻）

　　则剩下的序列还是满足最开始的条件，继续以同样的规则选择直到结束最后剩下010。

　　举例说明：

　　001010100

　　先取第一个1和旁边的0 变为 010100

　　取后面的1和旁边的0 变为 010 最后全部取走。

如果能想到上面的结论，剩下的就只是一个简单的DP了，DP[i][j] 表示取i块，最后一块序列为j的最大值，由于第一块和最后一块不能同时取，所以需要计算两次。其实和这道题蛮像的 https://leetcode-cn.com/problems/house-robber-ii/

class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size();
        int select = n / 3;
        int dp1[select + 1][n];
        int dp2[select + 1][n];
        memset(dp1, 0, sizeof dp1);
        memset(dp2, 0, sizeof dp2);
        dp1[1][0] = slices[0];
        dp2[1][1] = slices[1];
        for (int i = 1; i <= select; i++) {
            for (int j = 2; j < n; j++) {
                for (int k = 0; k < j - 1; k++) {
                    dp1[i][j] = max(dp1[i][j], dp1[i-1][k] + slices[j]);
                    dp2[i][j] = max(dp2[i][j], dp2[i-1][k] + slices[j]);
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < n - 1; i++) {
            ans = max(ans, dp1[select][i]);
        }
        for (int i = 0; i < n; i++) {
            ans = max(ans, dp2[select][i]);
        }
        return ans;
    }
};

三层循环可以简化为两层循环

class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size();
        int select = n / 3;
        int dp1[select + 1][n];
        int dp2[select + 1][n];
        memset(dp1, 0, sizeof dp1);
        memset(dp2, 0, sizeof dp2);
        dp1[1][0] = slices[0];
        dp2[1][1] = slices[1];
        int max1, max2;
        for (int i = 1; i <= select; i++) {
            max1 = dp1[i-1][0];
            max2 = dp2[i-1][0];
            for (int j = 2; j < n; j++) {
                dp1[i][j] = max1 + slices[j];
                dp2[i][j] = max2 + slices[j];
                max1 = max(max1, dp1[i-1][j-1]);
                max2 = max(max2, dp2[i-1][j-1]);
            }
        }
        int ans = 0;
        for (int i = 0; i < n - 1; i++) {
            ans = max(ans, dp1[select][i]);
        }
        for (int i = 0; i < n; i++) {
            ans = max(ans, dp2[select][i]);
        }
        return ans;
    }
};