解决方案|致拓T8数字化ERP
简介:通过快速构建敏捷ERP系统,实现从销售到财务的全流程闭环管理,助力企业数字化升级。
「致拓T8数字化ERP」解决方案聚焦业财一体,助力企业卓有成效地提升经营收益,赋能企业个性化数字生产管理。本解决方案由上海致拓数字科技有限公司提供。
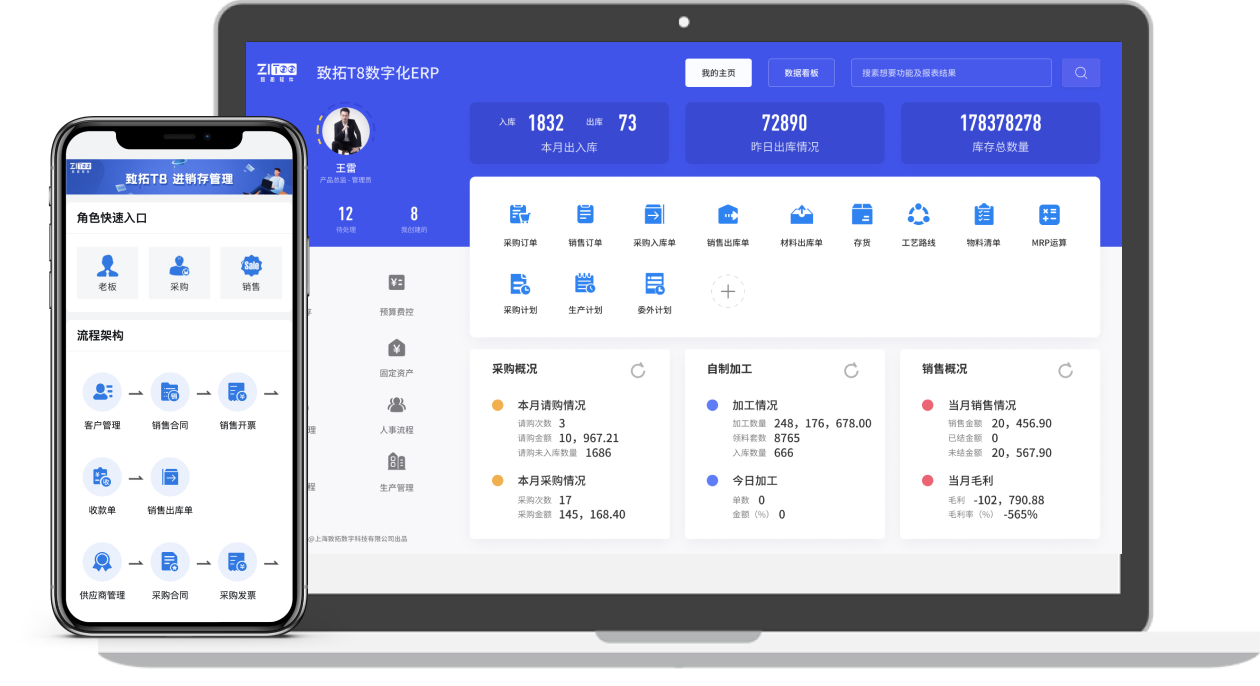
T8数字化ERP一览
01 您是否遇到传统业财一体的这些痛点

02 使用致拓ERP业财一体前后区别
通过快速构建敏捷的ERP系统,实现从销售到财务的全流程闭环管理,助力企业数字化升级。使企业协作效率更高,对库存订单状况了如指掌,并为管理者提供直观的数据可视化平台。

03 快速了解致拓ERP业财一体功能

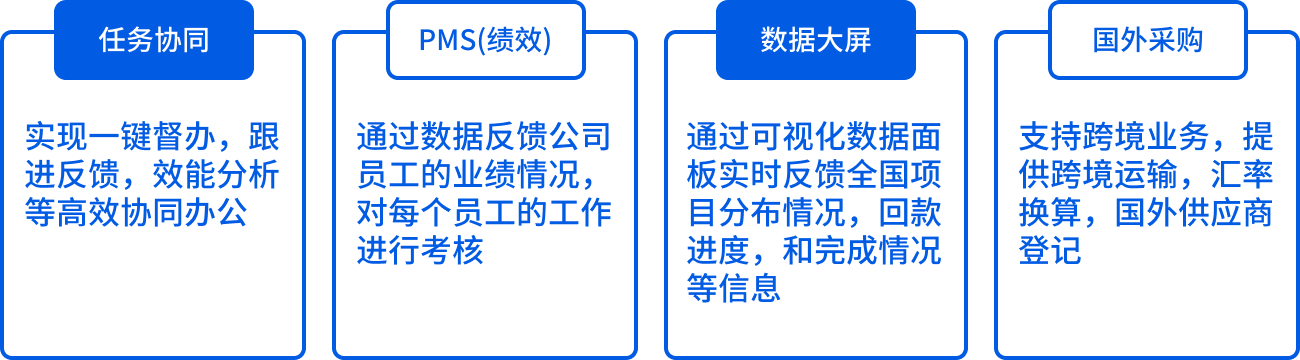
04 致拓数字化ERP亮点功能
致拓T8基于钉钉宜搭云钉低代码平台,能够为您的组织制定多元的IM场景群消息自动同步策略,实现:事事有反馈,件件有结果,一DING到底,再也不会遇到审批流程无进度,响应不及时,流程节点不清晰的情况。

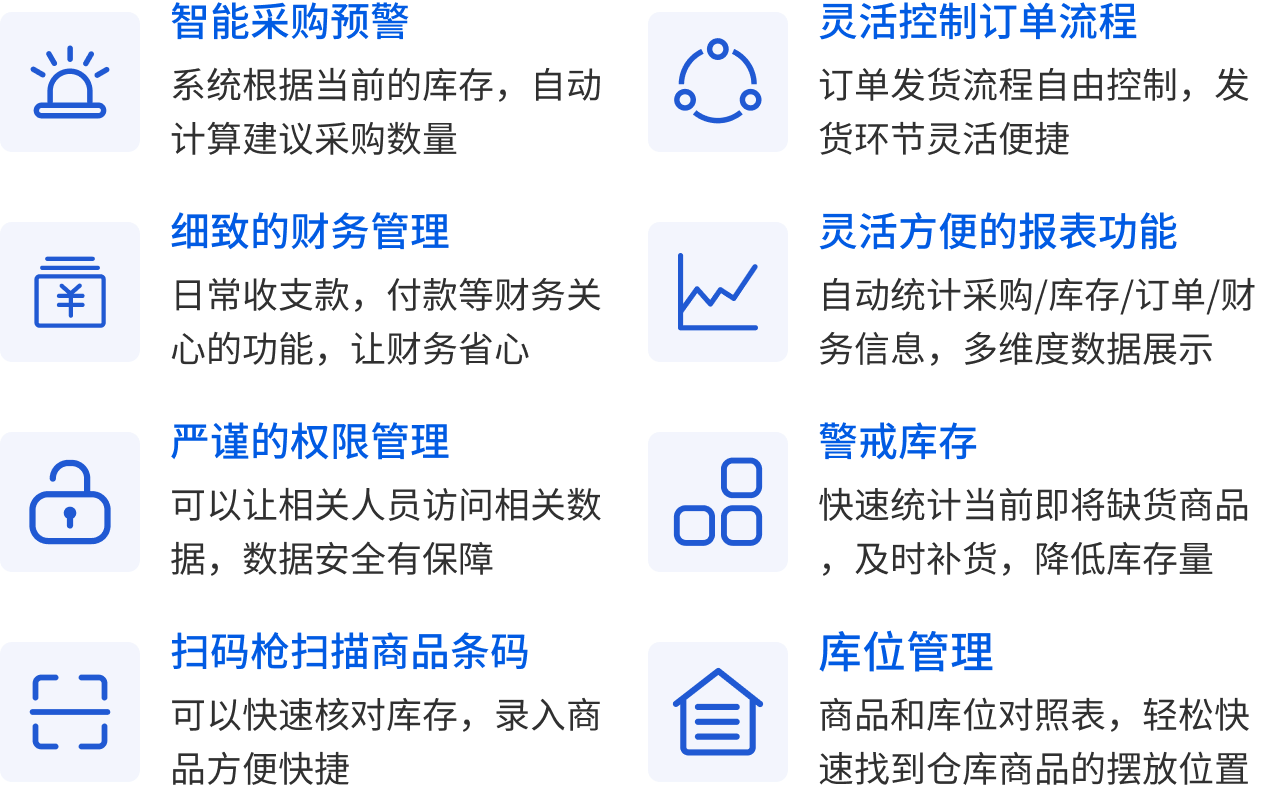
其他功能一览
05 简单4步走,三周即可上线使用

06 客户案例
案例一 某国外货船运输企业客户

客户是位于坦桑尼亚Dar Es Salaam的一家中资国际物流企业,客户之前用手工方式做数据统计和上报,导致管理层在做决策分析的时候得不到有效的数据支撑,企业实际经营情况不能及时反馈,盈利状态模糊。客户于2022年采购T8数字化系统后,通过数字化系统帮客户实现了经营分析前置,现金流量分析可视化,成本管控适量化,同时通过T8数字化系统与钉钉的深度融合,使企业员工的工作效率得到了显著提升。
上线时间:2022.01
使用后:客户成本降低40%;货物运输周期缩短60%
案例二 某医疗器械销售服务公司客户

客户属于科学研究和技术服务行业,希望能有一款简单、便捷的平台来帮助企业更好管理公司日常业务,规范员工操作流程。同时,能够实现与多方合作医院打通联系壁垒,实现高效合作,提升合作院方的售后体验。借助宜搭平台的T8数字化系统,实现了从经销商到院方,及整个医疗服务的信息与业务全业链贯通。
上线时间:2021.11
使用后:服务成本降低60%;签约成交上涨30%
案例三 某大型非标阀体制造企业上市公司客户

客户从事各类阀门的生产加工,货物进出口及技术进出口业务。随着近年来电商业务的兴起,传统的生产排单方式已不能满足企业的接单频率,随着订单源源不断地流入,数字化生产与排期的需求日益急切。致拓数字化ERP产品帮助公司做到了计划前置,生产前置,交货延期风险前置等,提供车间生产追踪管理能力,显著提升企业生产效率,降低企业生产成本。
上线时间:2021.10
使用后:车间用工成本降低20%;订单交付周期缩短15%~20%
本文为阿里云原创内容,未经允许不得转载。
解决方案|致拓T8数字化ERP的更多相关文章
- dynamics 365 AI 解决方案 —— 微软布局
核心提示:微软在 Office365.Azure 云.Dynamics365 上进行人工智能技术的部署,野心不小. 微软在2016年9月宣布组建自己的 AI 研究小组.该小组汇集了超过 5000 名计 ...
- ERP小金刚Pro专业大比拼: Dynamics,NetSuite和Odoo
前言 在过去的15年中,新技术推动了大大小企业的重新思考他们的流程管理涉及不断变化的业务所创造的新动态景观.实施ERP是许多企业为帮助组织而采取的措施并优化他们开展业务的方式.然而,市场上目前有许多商 ...
- 微软要如何击败Salesforce?Office365、Azure、Dynamics365 全面布局AI | 双语
微软在上月宣布组建自己的 AI 研究小组.该小组汇集了超过 5000 名计算机科学家和工程师,加上微软内部研究部门,将共同挖掘 AI 技术. 与此同时,亚马逊,Facebook,Google,IBM ...
- 开源ERP-成功案例分析(3)
Odoo用户概要 关于Odoo全球的用户,我们来看一些数据: Odoo目前全球有300万使用者 Odoo系统上每天新创建的数据库超过1000个 Odoo和Word.Excel.PowerPoint一样 ...
- 从SAP社区上的一篇博客开始,聊聊SAP产品命名背后的那份情怀
最近Jerry在SAP社区上看到一篇博客:It's Steampunk now. 博客原文:https://blogs.sap.com/2019/08/20/its-steampunk-now/ 什么 ...
- 利用预测分析改进欠款催收策略,控制欺诈风险和信贷风险—— Altair Knowledge Studio 预测分析和机器学习
前提摘要 在数字经济新时代,金融服务主管正在寻求方法去细分他们的产品和市场,保持与客户的联系,寻找能够推动增长和收入的新市场,并利用可以增加优势和降低风险的新技术. 在拥有了众多可用数据之后,金融机构 ...
- 一文带你读懂!华为云在ACMUG技术沙龙上都透露了些啥?
摘要:近日,华为云数据库业务总裁苏光牛在ACMUG中国MySQL用户组主办的 "华为云专场" 技术沙龙中分享了华为云数据库重磅新品GaussDB的核心能力与竞争优势.那么, Gau ...
- 铺路、建路、指路:联想ISG给出一份全新的智能化“路书”
新基建,新服务,新智能:联想给出的"高质量"方案 昨天,第七届联想创新科技大会(Lenovo Tech World 2021)正式召开.每年通过这个大会,各行各业不仅可以了解联想最 ...
- 海量数据分析更快、更稳、更准。GaussDB(for MySQL) HTAP只读分析特性详解
本文作者康祥,华为云数据库内核开发工程师,研究生阶段主要从事SPARQL查询优化相关工作.目前在华为公司参与华为云GaussDB(for MySQL) HTAP只读内核功能设计和研发. 1. 引言 H ...
- 项目实战:在线报价采购系统(React +SpreadJS+Echarts)
小伙伴们对采购系统肯定不陌生,小到出差路费.部门物资采购:大到生产计划.原料成本预估都会涉及到该系统. 管理人员可以通过采购系统减少管理成本,说是管理利器毫不过分,对于采购的效率提升也有极大帮助. 但 ...
随机推荐
- GCC&&G++ C && C++ 内嵌汇编和调用汇编函数的方法(x86,ARM自己对照改)
PS:要转载请注明出处,本人版权所有. PS: 这个只是基于<我自己>的理解, 如果和你的原则及想法相冲突,请谅解,勿喷. 前置说明 本文作为本人csdn blog的主站的备份.(Bl ...
- 【虚拟仿真】3DCAT虚拟仿真在化工安全方面的应用
随着中国经济的快速发展,石油化工企业的生产事故也在频繁发生.国家目前对生产安全的重视程度提高到前所未有的高度.企业也在安全管理上做了许多工作,如:进行安全培训,制定安全手册等.但这些方式的效果不明显, ...
- 5G+实时云渲染:交互实时云看车革新购车体验
随着科技的发展,用户的购车方式已然发生了改变. 传统的购车过程中,用户需要亲自去4S店看车.选车.预约试驾,最后完成交易. 互联网的发展和突如其来的疫情,让看车.选车.预约试驾这三个过程,逐步被搬到线 ...
- 深入浅出Java多线程(十三):阻塞队列
引言 大家好,我是你们的老伙计秀才!今天带来的是[深入浅出Java多线程]系列的第十三篇内容:阻塞队列.大家觉得有用请点赞,喜欢请关注!秀才在此谢过大家了!!! 在多线程编程的世界里,生产者-消费者问 ...
- RageFrame学习笔记:环境配置+项目拉取并实例化到本地
最近在研究一个基于YII2的框架,原本我以为很简单,但没想到在第一步环境配置和实例化上就卡了我4个小时,这里分享出我走过的弯路和解决问题的整个流程. 关注我文章的朋友应该了解过,我之前学习easyad ...
- node14.20.0安装pnpm5.15.0兼容
1,执行命令:npm install -g pnpm@5.15.0 2,设置淘宝镜像源: pnpm config set registry https://registry.npm.taobao.or ...
- cadence软件画版图操作
cadence软件操作 1.原理图设计 电路的原理图设计和许多的电路设计软件是类似的,这里大致介绍一下基本的操作. 首先是新建一个cell的原理图: library manager>file&g ...
- 可变形卷积系列(一) 打破常规,MSRA提出DCNv1 | ICCV 2017 Oral
论文提出可变形卷积帮助模型高效地学习几何变换能力,能够简单地应用到分类模型和检测模型中,思想新颖,效果显著,十分值得学习 来源:晓飞的算法工程笔记 公众号 论文: Deformable Convo ...
- KingbaseES 数据库使用Limit子句查询结果返回顺序不一致
一.KingbaseES数据库limit查询子句: 在KingbaseES数据库使用LIMIT子句限制查询结果的行数,从而实现分段显示数据的功能. 使用LIMIT子句在KingbaseES数据库中进行 ...
- KingbaseES V8R6 集群运维案例 -- 自动故障转移失败处理
KingbaseES V8R6版本 数据库自动故障转移失败(Automatic Database Failover Fails) 适用于: KingbaseES V8R6 版本. repmgr配置信息 ...
