机器学习-决策树系列-决策树-ID3算法 -C4.5算法-26

1. 决策树
2. 举个例子计算信息增益
3. C4.5算法

1. 决策树

决策树是属于有监督机器学习的一种，起源非常早，符合直觉并且非常直观，

模型生成：通过大量数据生成一颗非常好的树，用这棵树来预测新来的数据

预测：来一条新数据，按照生成好的树的标准，落到某一个叶子节点上

决策树的数学表达，递归自己调用自己

决策树的生成本质

就是数据不断分裂的递归过程，每一次分裂，尽可能让类别一样的数据在树的一边，当树的叶子节点的数据都是一类的时候，则停止分裂。

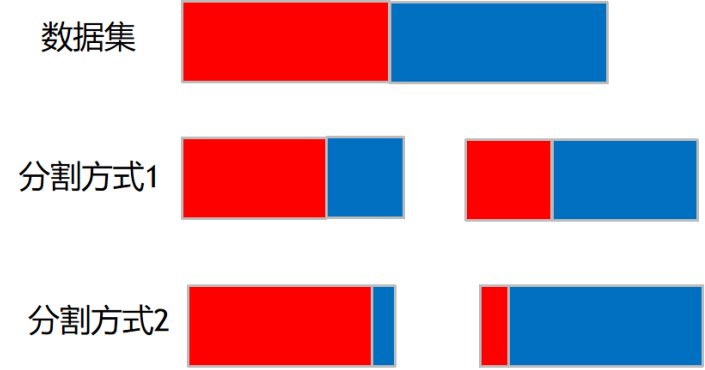
分裂好坏的评判的指标：基尼系数

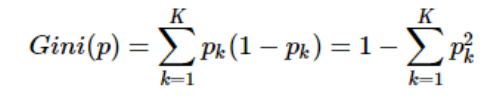
Gini系数越小，代表D集合中的数据越纯，所有我们可以计算分裂前的值

二分的场景：

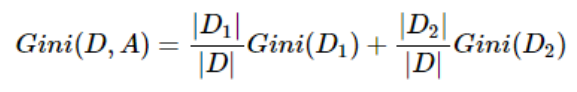
按照某个维度对数据集进行划分，然后可以去计算多个节点的Gini系数

分裂好坏的评判的指标：信息熵

在信息论里熵叫作信息量，即熵是对不确定性的度量。从控制论的角度来看，应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。他把信息定义为“用来消除不确定性的东西”。在信息世界，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。

举例说明，假设Kathy在买衣服的时候有颜色，尺寸，款式以及设计年份四种要求，而North只有颜色和尺寸的要求，那么在购买衣服这个层面上Kathy由于选择更多因而不确定性因素更大，最终Kathy所获取的信息更多，也就是熵更大。所以信息量=熵=不确定性，通俗易懂。在叙述决策树时我们用熵表示不纯度（Impurity）。

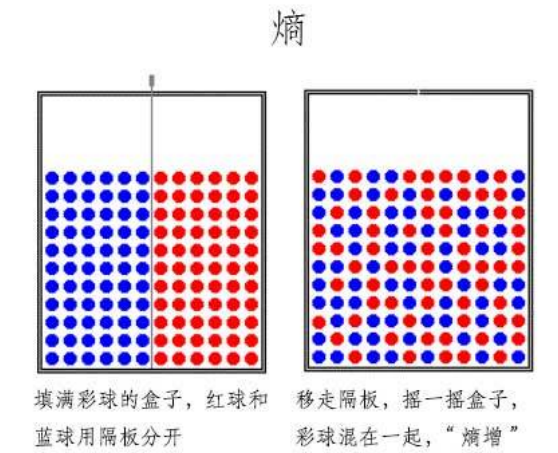
生命的本质在于抵抗熵增

打扫房间：让你周围的世界变得有序

吃饭：让你体内的分子变得有序那可不可以这样认为食物里面的熵更低 -->食物里面的更低的熵（更有序的分子排列）是谁实现的从哪里来的？-->植物的光合作用 -->分子的有序排列是需要消耗能量的

有序到无序的过程能量的耗散过程

无序到有序需要吸收能量才能实现

息论中熵的概念，熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：

举个例子，比如X有2个可能的取值，而这两个取值各为1/2时X的熵最大，此时X具有最大的不确定性：，

如果一个值概率大于1/2，另一个值概率小于1/2，则不确定性减少，对应的熵也会减少。比如一个概率1/3，一个概率2/3，则对应熵为：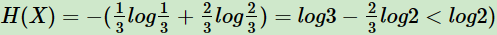

2. 举个例子计算信息增益

信息增益：分裂前的信息熵减去分裂后的信息熵一个分裂导致的信息增益越大，代表这次分裂提升的纯度越高

分裂前的减去分裂后的。

根节点没有分裂的时候：

根据性别分叉

性别这个维度分叉得到的信息增益：

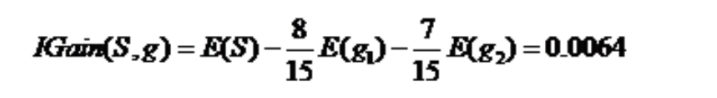
根据活跃度分裂：

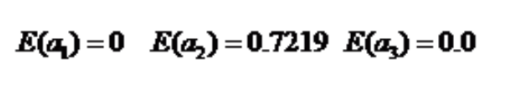
对应的信息增益：

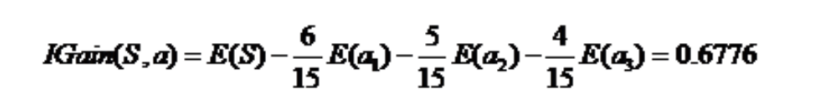
因此，根据活跃度来分叉是更优的

信息熵与Gini指数关系

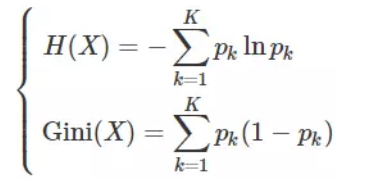
将 f(x) = −lnx 在 x = 1 处进行一阶泰勒展开

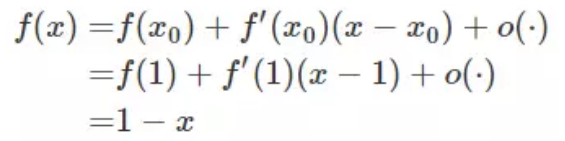
计算信息熵涉及log计算效率会慢很多因此很多时候是用gini系数去计算

以上方法叫做决策树ID3 其缺点：

ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如何校正这个问题呢？没有考虑过拟合的问题

ID3 算法的作者昆兰基于上述不足，对ID3算法做了改进，这就是C4.5算法

3. C4.5算法

ID3不足：一是不能处理连续特征，第二个就是用信息增益作为标准容易偏向于取值较多的特征，最后两个是缺失值处理的问和过拟合问题

息增益作为标准容易偏向于取值较多的特征的问题。我们引入一个信息增益比的变量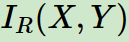

信息增益和特征熵的比值：

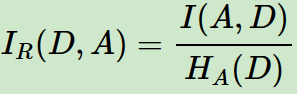
特征熵：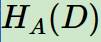

特征数越多的特征对应的特征熵越大，它作为分母，得到的信息增益比就会更小，校正信息增益容易偏向于取值较多的特征的问题。

C4.5虽然改进或者改善了ID3算法的几个主要的问题，仍然有优化的空间。

由于决策树算法非常容易过拟合，对于生成的决策树必须要进行剪枝。剪枝的算法有非常多，C4.5的剪枝方法有优化的空间。一种是预剪枝，另一个是后剪枝，即先生成决策树，再通过交叉验证来剪枝

C4.5由于使用了熵模型，里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算。

在CART树里面加以了改进，在普通的决策树算法里，CART算法算是比较优的算法了。