洛谷P1257 平面上的最接近点对

n<=10000个点，求欧几里德距离最小的一对点。

经典分治，把这些点按x排序，分成两半，每边分别算答案，答案是左边的最小，右边的最小，左右组起来的最小三者的最小。发现只有左右组的有点难写。

假设左右两半各自的最小中的最小是d，左半边最右的点横坐标是X1，右半边最左的点的横坐标是X2。那么只需要坐标在X1-d到X2+d的范围内的点找更小的距离。如下图。

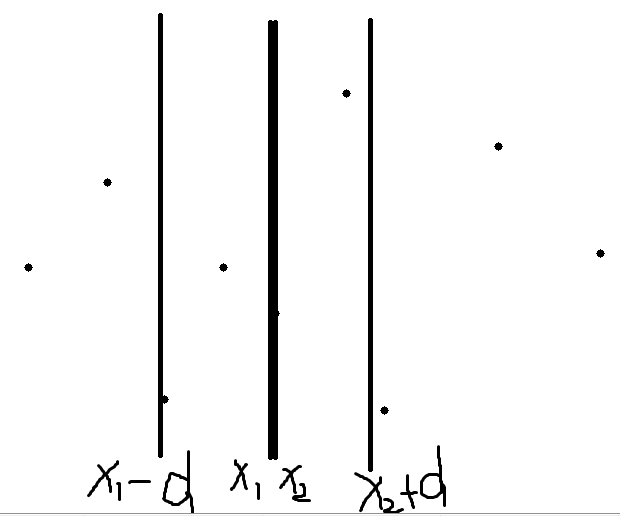
极端地，x1和x2相等时，x1上的某一个点最多可能和多少点组更小的距离呢？

假如左半边上在x1上有一个大大的点，那么右半边的点只有在圆形区域内才可能组成更小距离。而由于右边的点的最小距离不小于d，因此涉及到圆形区域对应的纵坐标范围的点最多有：

这样六个点，也就是说，比如左边那个点纵坐标y，只要在右边找到纵坐标大于等于y的第一个点，然后用它上下的六个点来和左边那个点凑更短的距离即可。这样，只需要把两半横坐标符合的点装进两个数组里，按y排序，两个指针扫一次即可。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cstdlib>
 #include<cmath>
 //#include<iostream>
 using namespace std;

 int n;
 #define maxn 10011
 struct Point
 {
     double x,y;
 }p[maxn],a[maxn],b[maxn];int la=,lb=;
 bool cmpx(const Point &a,const Point &b) {return a.x<b.x;}
 bool cmpy(const Point &a,const Point &b) {return a.y<b.y;}
 double sqr(double x) {return x*x;}
 double dis(const Point &a,const Point &b)
 {
     return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
 }
 double merge(int L,int R)
 {
     if (L==R) return 1e18;
     if (R-L==) return dis(p[L],p[R]);
     const int mid=(L+R)>>;
     double ans=min(merge(L,mid),merge(mid+,R));
     la=lb=;
     for (int i=L;i<=mid;i++) if (p[mid].x-p[i].x<=ans) a[++la].x=p[i].x,a[la].y=p[i].y;
     for (int i=mid+;i<=R;i++) if (p[i].x-p[mid+].x<=ans) b[++lb].x=p[i].x,b[lb].y=p[i].y;
     sort(a+,a++la,cmpy);sort(b+,b++lb,cmpy);
     int j=;
     for (int i=;i<=la;i++)
     {
         while (j<=lb && b[j].y<a[i].y) j++;
         for (int k=max(,j-);k<=min(lb,j+);k++) ans=min(ans,dis(a[i],b[k]));
     }
     return ans;
 }
 int main()
 {
     scanf("%d",&n);
     for (int i=;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
     sort(p+,p++n,cmpx);
     printf("%.4lf\n",merge(,n));
     return ;
 }