【BZOJ2301】Problem b（莫比乌斯反演）

题意：对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，

且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

思路：第一题反演……

利用容斥原理将原询问拆成4个，问题就转化为：

1<=i<=trunc(a div k)，1<=j<=trunc(b div k)，gcd(i,j)=1的(i,j)数对个数

令f(i)表示满足gcd(x,y)=i时(x,y)的对数，F(i)表示满足i|gcd(x,y)的(x,y)的对数

显然F(i)=trunc(n div i)*trunc(m div i)

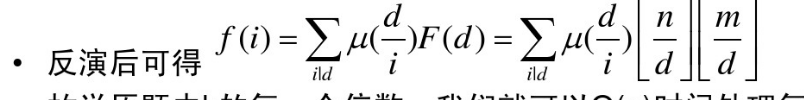
f(1)=sigma u(d)*n div d*m div d (1<=d<=n)

观察可得n div d*m div d只有2根号n个取值，且每个取值对应的u(i)是连续的一段

然后就可以记录u的前缀和来优化

From  http://m.blog.csdn.net/article/details?id=50590197

 //uses sysutils;
 const max=;
 var mu,sum,prime:array[..max]of longint;
     flag:array[..max]of longint;
     a,b,c,d,k,i,j,t,m,cas,v:longint;
     tmp:double;

 procedure swap(var x,y:longint);
 var t:int64;
 begin
  t:=x; x:=y; y:=t;
 end;

 function clac(n,m:longint):int64;
 var i,t1,t2,pos:longint;
     x,y:int64;
 begin
  if n>m then swap(n,m);
  clac:=; i:=;
  while i<=n do
  begin
   x:=n div i; y:=m div i;
   t1:=n div x;
   t2:=m div y;
   if t1<t2 then pos:=t1
    else pos:=t2;
   clac:=clac+x*y*(sum[pos]-sum[i-]);
   i:=pos+;
  end;
 end;

 begin
  assign(input,'bzoj2301.in'); reset(input);
  assign(output,'bzoj2301.out'); rewrite(output);
 // tmp:=now;
  read(cas);
  mu[]:=;
  for i:= to max do
  begin
   if flag[i]= then
   begin
    inc(m); prime[m]:=i;
    mu[i]:=-;
   end;
   j:=;
   while (j<=m)and(prime[j]*i<=max) do
   begin
    t:=prime[j]*i;
    flag[t]:=;
    if i mod prime[j]= then
    begin
     mu[t]:=;
     break;
    end;
    mu[t]:=-mu[i];
    inc(j);
   end;
  end;
  for i:= to max do sum[i]:=sum[i-]+mu[i];
  for v:= to cas do
  begin
   read(a,b,c,d,k);
   dec(a); dec(c);
   a:=a div k; b:=b div k; c:=c div k; d:=d div k;
   writeln(clac(b,d)-clac(b,c)-clac(a,d)+clac(a,c));
  end;
  //writeln((now-tmp)*::);
  close(input);
  close(output);
 end.

UPD（2018.10.22）：C++

 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef vector<int> VI;
 #define fi first
 #define se second
 #define MP make_pair
 #define N   51000
 #define M   410000
 #define eps 1e-8
 #define pi  acos(-1)
 #define oo  1e9

 int mu[N+],s[N+],prime[N+],flag[N+];

 ll calc(int n,int m)
 {
     if(n>m) swap(n,m);
     ll ans=;
     int i=;
     while(i<=n)
     {
         ll x=n/i;
         ll y=m/i;
         int t1=n/x;
         int t2=m/y;
         int pos=min(t1,t2);
         ans+=x*y*(s[pos]-s[i-]);
         i=pos+;
     }
     return ans;
 }

 int main()
 {
     int cas;
     scanf("%d",&cas);
     mu[]=;
     int m=;
     for(int i=;i<=N;i++)
     {
         if(!flag[i])
         {
             prime[++m]=i;
             mu[i]=-;
         }
         for(int j=;j<=m;j++)
         {
             int t=prime[j]*i;
             if(t>N) break;
             flag[t]=;
             if(i%prime[j]==)
             {
                 mu[t]=;
                 break;
             }
             mu[t]=-mu[i];
         }
     }
     for(int i=;i<=N;i++) s[i]=s[i-]+mu[i];
     while(cas--)
     {
         int a,b,c,d,k;
         scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
         a--; c--;
         a/=k; b/=k; c/=k; d/=k;
         ll ans=calc(b,d)-calc(b,c)-calc(a,d)+calc(a,c);
         printf("%lld\n",ans);
     }
     return ;
 }