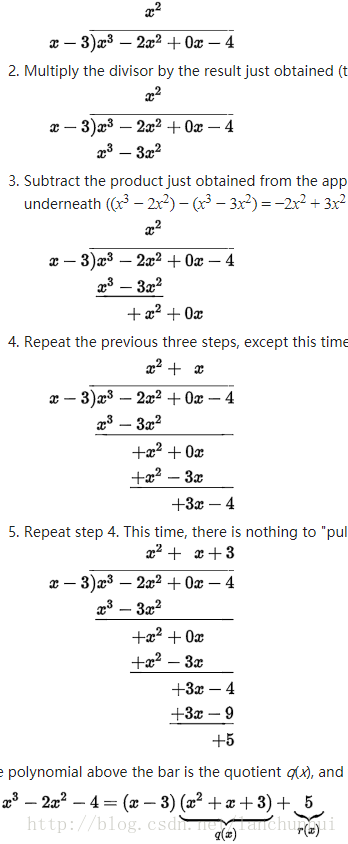(多项式)因式分解定理(Factor theorem)与多项式剩余定理(Polynomial remainder theorem)(多项式长除法)
(多项式的)因式分解定理(factor theorem)是多项式剩余定理的特殊情况,也就是余项为 0 的情形。
0. 多项式长除法(Polynomial long division)
Polynomial long division - Wikipedia
1. 因式分解定理
该定理表达的是,多项式 f(x) 存在因子 x−k 当且仅当 f(k)=0(余数为 0,也即 k 是其根)。
对于多项式 f(x)=x3+7x2+8x+2,
- x−1 是否为其因子?f(1)≠0
- x+1 是否为其因子?f(−1)=0,故为其因子;
(多项式除法)又有 x3+7x2+8x+2x+1=x2+6x+2,因此 x+1 与 x2+6x+2 均为其因子。
2. 多项式余项定理
举例对于多项式 f(x)=x3−12x2−42,当除数为 x−3 时,商为 x2−9x−27,余项为 −123。也即,f(x)=(x−3)(x2−9x−27)−123。因此 f(3)=−123。
更为一般地,对于二次多项式 f(x)=ax2+bx+c,有如下的等式变换:
所以:
(多项式)因式分解定理(Factor theorem)与多项式剩余定理(Polynomial remainder theorem)(多项式长除法)的更多相关文章
- DHU 1788 Chinese remainder theorem again 中国剩余定理
Chinese remainder theorem again Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 ...
- HDU 1788 Chinese remainder theorem again 中国剩余定理
题意: 给定n,AA 以下n个数m1,m2···mn 则有n条方程 res % m1 = m1-AA res % m2 = m2-AA 问res的最小值 直接上剩余定理,嘿嘿 #include< ...
- 2019牛客暑期多校训练营(第七场)D Number——实系数多项式因式分解定理
前置知识 代数基本定理 定理:每个次数 ≥ 1 复系数多项式在复数域中至少有一个跟. 由此推出,n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算).(只要不断把多项式除以(x-xa),即可 ...
- hdu 1788 Chinese remainder theorem again(最小公倍数)
Problem Description 我知道部分同学最近在看中国剩余定理,就这个定理本身,还是比较简单的: 假设m1,m2,-,mk两两互素,则下面同余方程组: x≡a1(mod m1) x≡a2( ...
- Chinese remainder theorem again(中国剩余定理)
C - Chinese remainder theorem again Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:% ...
- 《孙子算经》之"物不知数"题:中国剩余定理
1.<孙子算经>之"物不知数"题 今有物不知其数,三三数之剩二,五五数之剩七,七七数之剩二,问物几何? 2.中国剩余定理 定义: 设 a,b,m 都是整数. 如果 m ...
- POJ 1006 中国剩余定理
#include <cstdio> int main() { // freopen("in.txt","r",stdin); ; while(sca ...
- [TCO 2012 Round 3A Level3] CowsMooing (数论,中国剩余定理,同余方程)
题目:http://community.topcoder.com/stat?c=problem_statement&pm=12083 这道题还是挺耐想的(至少对我来说是这样).开始时我只会60 ...
- poj1006中国剩余定理
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 103506 Accepted: 31995 Des ...
随机推荐
- HDU6189 Law of Commutation (数论)
题意:输入n和a 定义m等于2的n次方 求1-m有多少数使得 a^b = b^a (mod m) 题解:先打表找规律 发现a为奇数的答案只有b = a这一种 (不知道为什么也不想知道为什么 当a为偶数 ...
- java基础——String的常用方法
java中String的常用方法 1.length() 字符串的长度 例:char chars[]={'a','b'.'c'}; String s=new String(chars); i nt le ...
- java命令行版的ATM
import java.util.*;public class Jatm{ static String user = "123"; static String password = ...
- libevent reference Mannual III--working with events
FYI: http://www.wangafu.net/~nickm/libevent-book/TOC.html Working with events Libevent’s basic unit ...
- 解决idea控制台打印乱码问题
idea控制台打印乱码,用起来总别扭,也是在网上搜索了一番,靠一点猜测解决了. 首先打开你自己的idea的安装目录下(即右键桌面图标,点击打开文件所在位置),然后找到idea.exe.vmoption ...
- Python3.0科学计算学习之类
类: Python中的类是一个抽象的概念,甚至比函数还要抽象.可以把它简单的看作是数据以及由存取.操作这些数据的方法所组成的一个集合.类是Python的核心概念,是面向对象编程的基础. 类有如下的优点 ...
- Django-Rest framework中文翻译-Request
REST framework的Request类扩展自标准的HttpRequest,增加了REST framework灵活的请求解析和请求验证支持. 请求解析 REST framework的Reques ...
- Q-criterion- definition and post-processing
Q-criterion Table of Contents 1. Q-Criterion 1.1. Q-criterion– Hunt, Wray & Moin 1988 1.2. Q cri ...
- 【OpenCV, MFC】利用MFC和OpenCV通过系统对话框打开和保存图片
打开图片: void CImageProDlg::OnImageopen() { // TODO: 在此添加命令处理程序代码 Invalidate(); CFileDialog dlg(TRUE, N ...
- Mongodb学习总结(2)——MongoDB与MySQL区别及其使用场景对比
对于只有SQL背景的人来说,想要深入研究NoSQL似乎是一个艰巨的任务,MySQL与MongoDB都是开源常用数据库,但是MySQL是传统的关系型数据库,MongoDB则是非关系型数据库,也叫文档型数 ...