POJ 1631 Bridging signals（LIS 二分法 高速方法）

Language:
Default

Bridging signals

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 10762		Accepted: 5899

Description

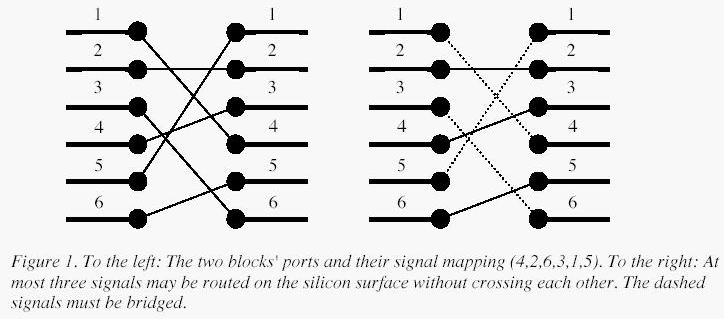
'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place.
At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to
bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports
at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers
in the range 1 to p, in which the i:th number specifies which port on the right side should be connected to the i:th port on the left side.Two signals cross if and only if the straight lines connecting the two ports of each pair do.

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then
follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

Source

Northwestern Europe 2003

因为数据太大。必需要用高速方法。我今天看这个看了好久。记住一点，c[i]代表长度为 i 的字串中，最后位最小的值

seach就是找寻以a[i]结尾的序列会有多长，然后就更新

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>

#define L(x) (x<<1)
#define R(x) (x<<1|1)
#define MID(x,y) ((x+y)>>1)

#define eps 1e-8
using namespace std;
#define N 100005

int a[N],c[N],n;

int seach(int len,int x)
{
	int le=0,ri=len,ans=0,mid;
	while(le<=ri)
	{
		mid=(le+ri)>>1;
		if(c[mid]<x)
		{
			ans=mid;
			le=mid+1;
		}
        else
			ri=mid-1;
	}
    return ans;
}
int main()
{
	int i,j,t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		for(i=1;i<=n;i++)
			scanf("%d",&a[i]);

		int len=1;
		c[1]=a[1];
		for(i=2;i<=n;i++)
		{
			if(a[i]>c[len])
			{
				j=len++;
			}
			else
			  j=seach(len,a[i]);
			c[j+1]=a[i];
		}
     printf("%d\n",len);
	}
   return 0;

}

版权声明：本文博主原创文章，博客，未经同意不得转载。