第三章 学习Shader所需的数学基础（4）

法线变换

法线（normal），也被称为法矢量（normal vector）。在以前我们已经讲过如何使用变换矩阵来变换一个顶点或方向矢量，但法线是需要我们特殊处理的一种方向矢量。在游戏中，模型的顶点往往会携带额外的信息，而顶点法线就是其中一种信息。当我们变换一个模型的时候，不仅需要变换它的顶点，还需要变换顶点法线，以便在后续处理（如片元着色器）中计算光照等。
一般来说，点和绝大部分方向矢量都可以使用同一个4×4或3×3的变换矩阵Ma->b把其从坐标空间A变换到坐标空间B中。但在变换法线的时候，如果使用同一个变换矩阵，可能就无法确保维持法线的垂直型。下面就来了解一下为什么会出现这样的问题。
我们先来了解另一种方向矢量——切线（tangent），也被称为切矢量（tangent vector）。与法线类似，切线往往也是模型顶点携带的一种信息。它通常与纹理空间对其，而且与法线方向垂直，如图所示。

由于切线是由两个顶点之间的差值计算得到的，因此我们可以直接使用用于变换顶点的变换矩阵来变换切线。假设，我们使用3×3变换矩阵Ma->b来变换顶点（注意，这里涉及到的变换矩阵都是3×3矩阵，不考虑平移变换，这因为切线和法线都是矢量，不会受平移影响），可以由下面的式子直接得到变换后的切线：

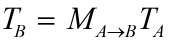
其中Ta和Tb分别表示在空间坐标A下和坐标空间B下的切线方向。但如果直接食用Ma->b来变换法线，得到的新的法线可能就不会与表面垂直了，下图给出了这样的一个例子：

那么，我们应该用哪个矩阵来变换法线呢？我们可以由数学约束条件来推出这个矩阵。我们知道一个顶点的切线Ta和法线Na必须满足垂直条件，即Ta·Na=0。给定变换矩阵Ma->b，我们已经知道Tb=Ma->bTa。我们现在想要找到一个矩阵G来变换法线Na，使得变换后的法线让然与切线垂直。即

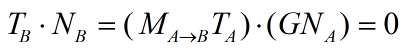
对上式进行一些推导可得

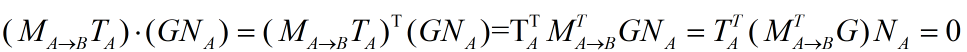
由于

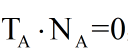
因此如果

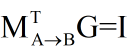
那么上式即可成立。也就是说如果

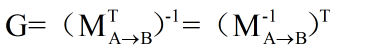
即使用原变换矩阵的逆转置矩阵来变换法线就可以得到正确的结果。
值得注意的是，如果变换矩阵Ma->b是正交矩阵，那么

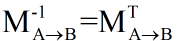
因此

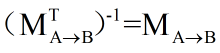
也就是说我们可以使用用于变换顶点的变换矩阵来直接变换法线。如果变换只包括旋转变换，那么这个变换矩阵就是正交矩阵。而如果变换只包含旋转和统一缩放，而不包含非统一缩放，我们利用统一缩放系数k来得到变换矩阵Ma->b的逆转置矩阵

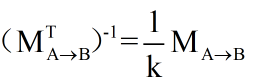
这样就可以避免计算逆矩阵的过程。而如果变换中包含了非统一的变换，那么我们就必须要求解逆矩阵来得到变换法线的矩阵。