【深度学习】K-L 散度，JS散度，Wasserstein距离

度量两个分布之间的差异

---

（一）K-L 散度

K-L 散度在信息系统中称为相对熵，可以用来量化两种概率分布 P 和 Q 之间的差异，它是非对称性的度量。在概率学和统计学上，我们经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息量。一般情况下，P 表示数据的真实分布，Q 表示数据的理论分布，估计的模型分布或者 P 的近似分布。

（二）K-L 散度公式

​ Note：KL 散度仅当概率 \(P\) 和 \(Q\) 各自总和均为1，且对于任何 \(i\) 皆满足 \(Q(i)>0\) ， \(P(i)>0\) 时，才有定义。

\[
D_{KL}(P||Q) = - \sum_i P(i) \ln \frac{Q(i)}{P(i)} = \sum_i P(i) \ln \frac{P(i)}{Q(i)}
\]

（三）使用 K-L 散度对比两种分布

​ 假设真实分布为 \(P\)，\(P\) 的两个近似分布为 \(Q_1, Q_2\)，对于这两个近似分布我们应该选择哪一个？K-L 散度可以解决这个问题：如果 \(D_{KL}(P||Q_1) < D_{KL}(P||Q_2)\)，那么我们选择 \(Q_1\) 作为 \(P\) 的近似分布。

（四）散度并非距离

​ 我们不能把 K-L 散度看作是两个分布之间距离的度量。首先距离度量需要满足对称性，但是 K-L 散度不具备对称性，即：
\[
D_{KL}(P||Q) \neq D_{KL}(Q||P)
\]

---

（五）问答环节

Q1：信息熵，交叉熵，相对熵的区别是什么？

A1：（1）信息熵，即熵，是编码方案完美时的最短平均编码长度；（2）交叉熵，即 Cross Entropy，是编码方案不一定完美时（对概率分布的估计不一定正确）的平均编码长度，在神经网络中常用作损失函数；（3）相对熵，即 K-L 散度，是编码方案不一定完美时，平均编码长度相对于最短平均编码长度的增加值。简单推理：

Q2：为什么在深度学习中使用 Cross Entropy 损失函数，而不是 K-L 散度？

A2：首先，损失函数的功能是衡量由样本计算所得的分布与目标分布之间的差异。在分布差异计算中，K-L散度是最合适的。但在实际中，某一事件的标签是已知不变的（比如猫狗分类中，猫的标签是1，那么数据集中所有关于猫的标签都要标记为1），即目标分布的熵为常数。根据公式：K-L散度 - 目标分布熵 = 交叉熵（这里的 - 代表裁剪），所以我们不用计算K-L散度，只需计算交叉熵就可以得到模型分布与目标分布的损失值。
换句话说，通常一个标签都是设置为 one-hot 模式，即我们常说的硬分布，\(\log1=0\)，所以一般都是只用交叉熵。如果标签不是这样的硬分布，而是软分布（比如有两张猫的图片，一张预测为0.6，另一张预测为0.8），K-L散度才能发挥比较好的作用。

Q3：K-L散度和JS散度存在什么问题？有什么解决方法？

A3：如果两个分布 \(P\) 和 \(Q\) 相离很远，甚至完全没有重叠，那么 K-L 散度值是没有意义的，而 JS 散度值是一个常数，意味着梯度为0，即发生了梯度消失，这在学习算法中是非常严重的问题。Wasserstein距离 （又名推土机距离）的提出就是为了解决这个问题，它的优越性在于即使两个分布没有重叠，Wasserstein 距离仍然能够反映它们的远近。以下图为例：

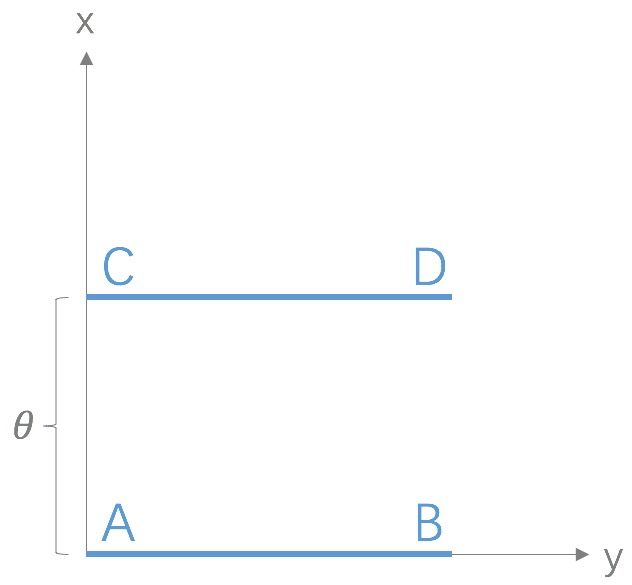
以上是二维空间中的两个分布 \(P_1\) 和 \(P_2\)，\(P_1\) 在线段 AB 上均匀分布，\(P_2\) 在线段 CD 上均匀分布，通过参数 \(\theta\) 控制两个分布的距离远近，由以上公式容易得到：

K-L 散度：

\[
D_{KL}(P_1||P_2)=
\begin{cases}
+ \infin & \text{if} & \theta \neq 0 \\
0 & \text{if} & \theta = 0 \\
\end{cases}
\]

JS 散度：

\[
JS(P_1||P_2)=
\begin{cases}
\log2 & \text{if} & \theta \neq 0 \\
0 & \text{if} & \theta = 0 \\
\end{cases}
\]

Wasserstein 距离：
\[
W(P_0, P_1) = |\theta|
\]
观察以上公式可知，K-L 散度和 JS 散度取值是突变的，要么最大要么最小，Wasserstein 距离却是平滑的。如果我们要用梯度下降法优化 \(\theta\) 这个参数，前两者根本提供不了梯度，Wasserstein 距离却可以。类似地，在高维空间中如果两个分布不重叠或者重叠部分可忽略，则 KL 和 JS 既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度。

---

References:

​ [1] 如何理解K-L散度（相对熵）

​ [2] 相对熵——维基百科

​ [3] 交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）