机器学习实战之logistic回归分类

利用logistic回归进行分类的主要思想：根据现有数据对分类边界建立回归公式，并以此进行分类。

logistic优缺点：

优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。 .
适用数据类型：数值型和标称型数据。

sigmoid函数：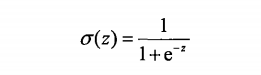

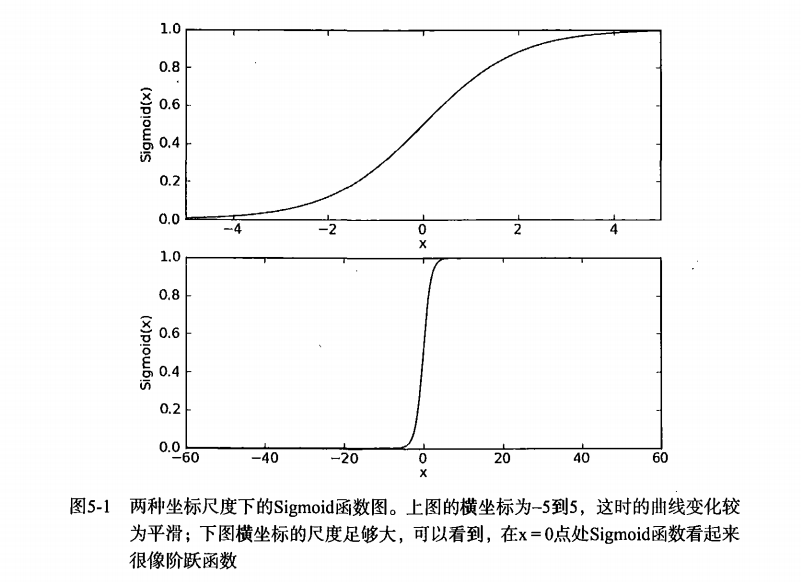
梯度上升法：

梯度：

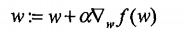
该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算
法达到某个可以允许的误差范围。

随机梯度上升法：

梯度上升算法在每次更新回归系数时都需要遍历整个数据集, 该方法在处理100个左右的数
据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种
改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新
样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与 “ 在线学
习”相对应，一次处理所有数据被称作是“批处理” 。

梯度下降法：

你最经常听到的应该是梯度下降算法，它与这里的梯度上升算法是一样的，只是公式中的
加法需要变成减法。因此，对应的公式可以写成: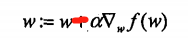

梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。

logistic预测疝气病预测病马的死亡率代码：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import random

# 加载数据集
def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('./testSet.txt')
    for line in fr.readlines():
        lineData = line.strip().split()
        dataMat.append([1.0, float(lineData[0]), float(lineData[1])])
        labelMat.append(int(lineData[2]))
    return dataMat, labelMat

# sigmoid 函数
def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

# 梯度上升
def gradAscent(dataMatIn, classLabels, maxCycles):
    dataMatrix = np.mat(dataMatIn)
    labelsMatrix = np.mat(classLabels).transpose() # 转置，将行向量转置为列向量
    m, n = np.shape(dataMatrix)

    alpha = 0.001
    W = np.ones((n, 1))
    for i in range(maxCycles):
        h = sigmoid(dataMatrix * W) # (100, 1)
        error = labelsMatrix - h # (100, 1)
        W = W + alpha * dataMatrix.transpose() * error # (3, 100) * (100, 1)

    return W 

#改进版随机梯度上升
def stocGradAscent1(dataMatrixIn, classLabels, numIter=150):
    dataMatrix = np.array(dataMatrixIn)
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4.0/(1.0+j+i)+0.01    #apha decreases with iteration, does not
            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return np.mat(weights.reshape(n, 1))

def plotBestFit(weights, dataMat, labelMat):
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if labelMat[i] == 1:
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker = 's')
    ax.scatter(xcord2, ycord2, s = 30, c = 'green')
    x = np.arange(-4.0, 4.0, 0.1)
    y = ((np.array((-weights[0] - weights[1] * x) / weights[2]))[0]).transpose()
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

# 预测
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

# 对训练集进行训练，并且对测试集进行测试
def colicTest():
    trainFile = open('horseColicTraining.txt')
    testFile = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in trainFile.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))

    # 开始训练
    weights = stocGradAscent1(trainingSet, trainingLabels, 400)
    errorCount = 0.0
    numTestVec = 0.0
    for line in testFile.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), weights)) != int(currLine[21]):
            errorCount += 1.0
    errorRate = errorCount / float(numTestVec)
    print("the error rate is:%f" % errorRate)
    return errorRate

# 多次测试求平均值
def multiTest():
    testTimes = 10
    errorRateSum = 0.0
    for i in range(testTimes):
        errorRateSum += colicTest()
    print("the average error rate is:%f" % (errorRateSum / float(testTimes)))

multiTest()