UVA 1473 Dome of Circus

https://cn.vjudge.net/problem/UVA-1473

题目

给出一些点，问包含这些点的最小圆锥（要求顶点在y轴，底面圆心在原点）的体积

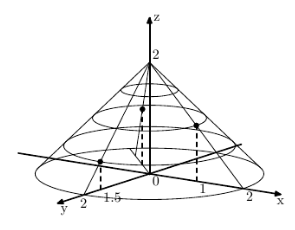
题解

因为圆锥对称，所以可以把所有点旋转到xOy平面，然后问题转化成求最小的三角形。

于是我们就可以求出上凸包，然后最小的三角形显然过凸包上的一个或两个点

过一个点的时候可以推公式：

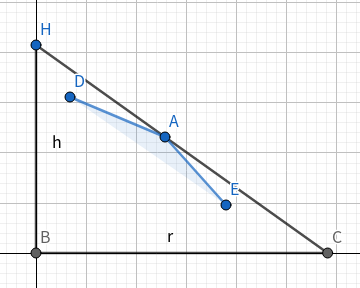
设$A(a,b),H(0,y),C(x,0)$

那么\[\frac{b}{x-a}=\frac{y}{x}\]

\[\pi x^2\times y/3 = C\times \frac{x^3}{x-a}\]

然后求导，得

\[\frac{3x^2(x-a)-x^3}{(x-a)^2}\]

符号只与分子有关

得$x=\frac{3a}{2}$时体积最小，其他时候体积都比这个大，偏得越多越大

然后还要考虑不能和上凸包的边相交

就这样就可以了，然后头晕写了个通过截面面积判断圆锥体积……

AC代码

#include<cstdio>
#include<cmath>
#include<cassert>
#include<algorithm>
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) void(0)
#endif
using namespace std;

#define EPS 1e-10
int dcmp(const double &x) {
	return fabs(x)<EPS?0:(x<0?-1:1);
}
inline double pf(double x) {
	return x*x;
}
#define MAXN 10007
template <class T, int S>
struct array {
	int n;
	T arr[S];
	T& operator[](int i) {return arr[i];}
};
struct dian {
	double x,y;
	bool operator<(const dian&r) const {
		return x>r.x || (dcmp(x-r.x)==0 && y<r.y);
	}
	bool operator==(const dian&r) const {
		return fabs(x-r.x)<EPS && fabs(y-r.y)<EPS;
	}
} dots[MAXN], vec;

dian operator-(const dian&a, const dian&b) {
	return (dian){a.x-b.x,a.y-b.y};
}

double Cross(const dian&l, const dian&r) {
	return l.x*r.y-l.y*r.x;
}

array<dian, MAXN> convex;

int main() {
	int n;
	while(~scanf("%d", &n)) {
		double x,y,z;
		convex.n=0;
		REP(i,0,n) {
			scanf("%lf%lf%lf", &x, &y, &z);
			dots[i].x=sqrt(pf(x)+pf(y));
			dots[i].y=z;
		}
		sort(dots,dots+n);
		n=unique(dots,dots+n)-dots;
		REP(i,0,n) {
			while(convex.n>=2 && dcmp(Cross(convex[convex.n-1]-convex[convex.n-2],dots[i]-convex[convex.n-2]))<=0) convex.n--;
			convex[convex.n++]=dots[i];
		}
		double ans=2e33;
		double r,h;
		REP(i,0,convex.n) {
			double tr,th,nans;
			tr=convex[i].x*1.5; th=convex[i].y*3;
			if(i>0 && dcmp(convex[i].y-convex[i-1].y)<=0) break;
			if(i>0 && dcmp(Cross(convex[i]-convex[i-1],(dian){-tr,th}))<0) {
				tr=Cross(convex[i],convex[i-1])/(convex[i-1].y-convex[i].y),
				th=Cross(convex[i],convex[i-1])/(convex[i].x-convex[i-1].x);
			}
			else if(i<convex.n &&
					dcmp(Cross(convex[i+1]-convex[i],(dian){-tr,th}))>0) {
				tr=Cross(convex[i+1],convex[i])/(convex[i].y-convex[i+1].y),
				th=Cross(convex[i+1],convex[i])/(convex[i+1].x-convex[i].x);
			}
			nans=tr*tr*th/2;
			if(nans>EPS && nans<ans) {
				ans=nans; r=tr; h=th;
			}
		}
		printf("%.3f %.3f\n", h,r);
	}
	return 0;
}