嵊州D2T3 玛利亚∙多斯普拉泽雷斯 完美配对

嵊州D2T3

玛利亚∙多斯普拉泽雷斯

公墓一共有 n 个墓地，通过 n − 1 条通道相连。

每次，推销员可以在选择一个墓地推销给玛利亚。

但是，考虑很多的玛利亚会尽量否决这个提议。

她会选择一个墓地，否决掉它和与它相连的墓地。

但为了礼仪，玛利亚不会选择推销员推销的或者已经被否决的墓地。

同样，为了礼仪，推销员也不会推销已经被否决的墓地。

如果某个被推销的墓地没有被否决，那么销售员就胜利了。

否则玛利亚就胜利了。

除此之外，玛利亚可以在任意时间以洪水为借口删除一些通道，每次删除的通道数量也是任意的，不过删除的通道总数不能超过 K。

两个墓地相连意味着这两个墓地由一条通道直接连接。

请判断双方都在最优策略下，谁能获胜。

Input

第一行两个整数 n, K，表示墓地数和允许删除的通道数量。

接下来 n−1 行，每行两个整数 ui , vi，表示 ui 号墓地与 vi 号墓地之间有一条通道。

Output

输出一行。

如果推销员胜利，输出’salesman’，否则输出’Maria’（不包括引号）。

Examples

cemetery.in	cemetery.out
2 1 1 2	Maria

Notes

对于所有数据，满足 0 ≤ K < n ≤ 5000。

Subtask1[10pts]

n ≤ 3

Subtask2[25pts]

n ≤ 6

Subtask3[30pts]

K = 0

Subtask4[35pts]

无特殊限制

---

Solve！

自言自语

我看完Solution后，想很煞笔的说句：

我怎么没听过“博弈”呀？

原来，是我蒻爆了。。。

题目解析

A:salesman　　B:Maria

给出一棵树

每次 A 可以选择一个点染 A

B 可以选择一个点把它和与它相邻的点染 B

B 可以在任何时候去掉一些边，

但总数不超过一个定值k

染过的点不能选择，但是染色标记可以覆盖

若最后所有点都染 B 色，B 赢，否则 A 赢

解题思路

这种题目可以按照Subtask一个一个想

Subtask1[10pts]

n ≤ 3

几个分类讨论就好啦

Subtask2[25pts]

n ≤ 6

首先可以发现边不管什么时候去掉 都是一样的

所以可以先枚举去边的情况，再进行搜索

Subtask3[30pts]

K = 0

可以发现，当且仅当 n = 2，赢

Subtask4[35pts]

无特殊限制

若原树不存在完美匹配，A 一定赢

A 每次操作可以强迫 B 和他一起染掉一个匹配

最后肯定会剩下孤立点，A 再选这个点就是 A 色了

若存在，A 可以第一步强迫 B 破坏掉完美匹配的性质，依然 A 赢

结论 2：若 K = 0 , N ≥ 3，A 赢

但是我还是想知道：

完美匹配又是什么呢？

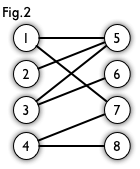
在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。

例如，图 3、图 4 中红色的边就是图 2 的匹配。

A 每次操作可以强迫 B 和他一起染掉一个匹配

最后肯定会剩下孤立点，A 再选这个点就是 A 色了

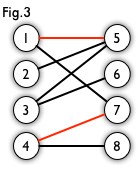
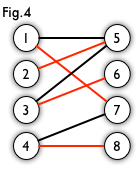
(图片来源：http://www.renfei.org/blog/bipartite-matching.html)

举例来说：

如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。

是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？

图论中，这就是完美匹配问题。

如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？

这就是最大匹配问题。

就是说，你要把一堆的点的连线中，删去一些，最后要求：每个点有且仅有一个出边。

所以他们要两两双向思嘛~呵呵呵o(*￣︶￣*)o

但是，怎么求他们能不能两两配对嘛……

我瞄了一眼题解

Std代码不对应，请忽略！

#include <cstdio>
#include <algorithm>
#include <vector>
#define FOR(i, l, r) for(int i = l; i <= r; ++i)
#define mp(x, y) make_pair(x, y)
using namespace std;
typedef long long ll;
const int N = ;
const ll inf = 1e15;
struct edge{int u, v, lim;} e[N];
bool operator < (edge a, edge b) {return a.lim < b.lim;}
vector<pair<int, ll> > ans;
int n, m, Q, x;
int fa[N], a[N], og[N];
ll up[N];
int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}
int main()
{
    freopen("poisoning.in" , "r" , stdin);
    freopen("poisoning.out" , "w", stdout);

    scanf("%d%d%d", &n, &m, &Q);
    FOR(i, , n)
    {
        scanf("%d", a + i);
        ans.push_back(mp(, a[i]));
    }
    FOR(i, , m) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].lim);
    FOR(i, , n) fa[i] = i, up[i] = a[i], og[i] = ;
    sort(e + , e + m + );
    FOR(i, , m)
    {
        int p = find(e[i].u), q = find(e[i].v);
        if (p == q) continue;
        og[q] = min(max((ll)og[p], e[i].lim - up[p]), max((ll)og[q], e[i].lim - up[q]));
        up[q] += up[p]; fa[p] = q; ans.push_back(mp(og[q], up[q]));
    }
    sort(ans.begin(), ans.end());
    for(int i = ; i < ans.size(); ++i)
        ans[i].second = max(ans[i].second, ans[i - ].second);
    while (Q--)
    {
        scanf("%d", &x);
        printf("%d\n", (--upper_bound(ans.begin(), ans.end(), make_pair(x, inf))) -> second + x);
    }
    return ;
}

Std

？？？

又用了STL？

看来std是个高手呀！

for循环都懒得写了，哼╭(╯^╰)╮

---

回到本源

若原树存在完美匹配

如果 B 能通过切边，把所有匹配都分割开来，B 赢，

否则 A 赢 充分性显然 A 选一个点，B 选与他匹配的一个点就好了

必要性： 如果不能完全分隔开，必然留下一个连通块，K = 0 , n > 2

由结论 2，A 赢

所以，贪心看下树有没有完美匹配就好了

时间复杂度 O(n)

5000 是用来吓唬人的？！？！？！

OK！