java实现Floyd算法

1 问题描述

何为Floyd算法？

Floyd算法功能：给定一个加权连通图，求取从每一个顶点到其它所有顶点之间的最短距离。（PS：其实现功能也称完全最短路径问题）

Floyd算法思想：将顶点i到j的直接距离依次与顶点i到顶点j之间加入k个中间节点之后的距离进行比较，从中选出最短的一组距离，即为顶点i到顶点j的最短距离，然后重复上述步骤求取其它顶点之间的最短距离。

2 解决方案

2.1 使用Floyd算法得到最短距离示例

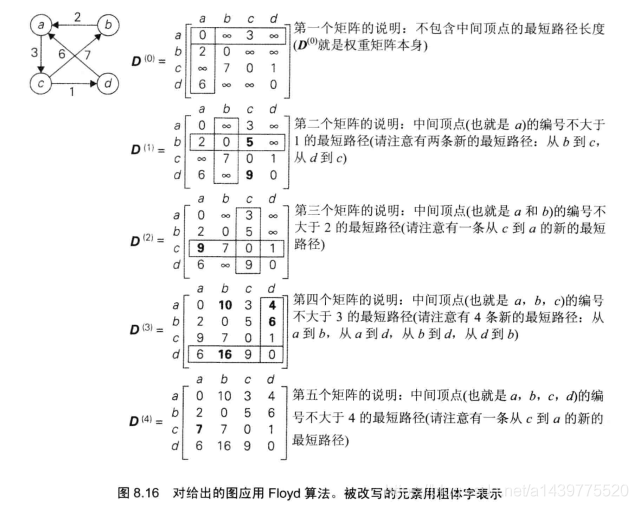
此处借用《算法设计与分析基础》第3版上一个插图：

其中，

D(0)表示不包含中间节点，即给定图的原始权重矩阵；

D(1)表示加入一个中间节点a；

D(2)表示在D(1)的基础上再加入一个中间节点b；

D(3)表示在D(2)的基础上再加入一个中间节点c；

D(4)表示在D(3)的基础上再加入一个中间节点d，这时就可得到最终结果。

每次加入一个中间节点后，都要更新所有顶点之间的最短距离，直到所有顶点均可以作为中间顶点之后，才算更新完毕，即可得到最终结果。

2.2 具体编码

Floyd是计算每对顶点间最短路径的经典算法，其采用的思想是动态规划法。

时间复杂度是雷打不动的O(n^3)。

注意，Floyd算法计算最短距离可以有负权值的边，但不能有权值和为负数的回路。

下面代码中所用图的数据便是2.1中示例图的数据。

package com.liuzhen.chapter9;

public class Floyd {
    /*
     * 参数adjMatrix：给定连通图的权重矩阵，其中权重为-1表示两个顶点不能直接相连
     * 函数功能：返回所有顶点之间的最短距离权重矩阵
     */
    public void getShortestPaths(int[][] adjMatrix) {
        for(int k = 0;k < adjMatrix.length;k++) {
            for(int i = 0;i < adjMatrix.length;i++) {
                for(int j = 0;j < adjMatrix.length;j++) {
                    if(adjMatrix[i][k] != -1 && adjMatrix[k][j] != -1) {
                        int temp = adjMatrix[i][k] + adjMatrix[k][j];  //含有中间节点k的顶点i到顶点j的距离
                        if(adjMatrix[i][j] == -1 || adjMatrix[i][j] > temp)
                            adjMatrix[i][j] = temp;
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        Floyd test = new Floyd();
        int[][] adjMatrix = {{0,-1,3,-1},
                {2,0,-1,-1},
                {-1,7,0,1},
                {6,-1,-1,0}};
        test.getShortestPaths(adjMatrix);
        System.out.println("使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为：");
        for(int i = 0;i < adjMatrix.length;i++) {
            for(int j = 0;j < adjMatrix[0].length;j++)
                System.out.print(adjMatrix[i][j]+" ");
            System.out.println();
        }
    }
}

运行结果：

使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为：
0 10 3 4
2 0 5 6
7 7 0 1
6 16 9 0