【Python脚本】刚度矩阵格式转换

对于1-2-3坐标系:

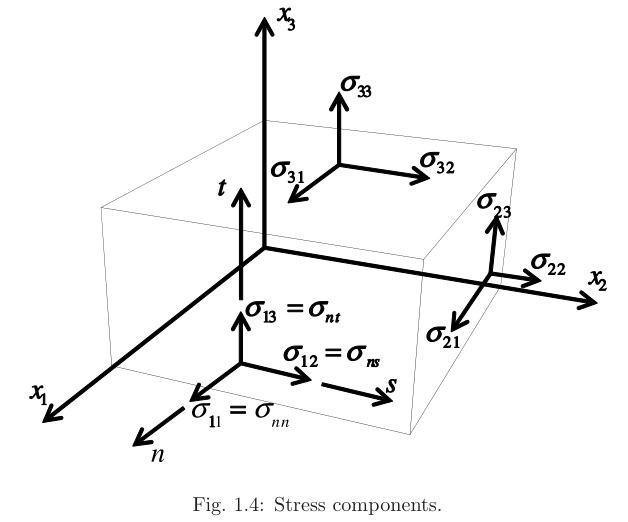
应力矩阵如下:

\[\left.[\sigma]=\left[\begin{array}{ccc}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{12}&\sigma_{22}&\sigma_{23}\\\sigma_{13}&\sigma_{23}&\sigma_{33}\end{array}\right.\right]
\]

张量应变矩阵如下:

\[\left.[\varepsilon]=\left[\begin{array}{ccc}\varepsilon_{11}&\varepsilon_{12}&\varepsilon_{13}\\\varepsilon_{12}&\varepsilon_{22}&\varepsilon_{23}\\\varepsilon_{13}&\varepsilon_{23}&\varepsilon_{33}\end{array}\right.\right]
\]

工程剪应变\(\gamma=2*\varepsilon\)

实际使用中会写成向量的形式:

\[应力向量\boldsymbol{\sigma}=[\sigma_{1} \quad \sigma_{2} \quad \sigma_{3} \quad \tau_{4} \quad \tau_{5} \quad \tau_{6}]
\]

\[应变向量\boldsymbol{\epsilon}=[\epsilon_{1} \quad \epsilon_{2} \quad \epsilon_{3} \quad \gamma_{4} \quad \gamma_{5} \quad \gamma_{6}]
\]

但是不同的商业软件,书籍中,应力/应变向量的含义并不完全一致,导致刚度柔度矩阵需要注意区分.

在<<复合材料力学>>胡更开第二版,以及<>Robert M.Jones 第二版中,应力/应变的简写表示为:

\[\begin{matrix} \sigma_{11} \rightarrow \sigma_1 & \epsilon_{11} \rightarrow \epsilon_1 \\ \sigma_{22} \rightarrow \sigma_2 & \epsilon_{22} \rightarrow \epsilon_2 \\ \sigma_{33} \rightarrow \sigma_3 & \epsilon_{33} \rightarrow \epsilon_3 \\ \tau_{23} \rightarrow \sigma_4 & \gamma_{23}=2\epsilon_{23} \rightarrow \epsilon_4 \\ \tau_{13} \rightarrow \sigma_5 & \gamma_{13}=2\epsilon_{13} \rightarrow \epsilon_5 \\ \tau_{12} \rightarrow \sigma_6 &\gamma_{12}=2\epsilon_{12} \rightarrow \epsilon_6 \end{matrix}
\]

以上可以称为"Standard Convention"

其他商业软件中的conventions:

根据上表,可愿意定义一个转换矩阵T,将应变应力从标准Voigt形式转换到Abaqus,Ls-dyna,Ansys等软件的应力应变形式:

\[\{\sigma_A\}=[T]\{\sigma\}
\]

\[[T]=\left[\begin{array}{cccccc}1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&1\\0&0&0&0&1&0\\0&0&0&1&0&0\end{array}\right]
\]

使用以上的T矩阵,就可以将应变应力从标准张量形式转换到Abaqus的notation.此外,刚度矩阵的转换为:

\[[C_A]=[T]^T[C][T]
\]

For LS-DYNAand ANSYS, the transformation matrix is:

\[[T]=\left[\begin{array}{cccccc}1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&1\\0&0&0&1&0&0\\0&0&0&0&1&0\end{array}\right]
\]

Code

根据以上公式,可以写出转换代码:

def tMatrix(target:str='abq-sta')->np.ndarray:
    """定义一个转换矩阵T,将应变应力从标准Voigt形式转换到Abaqus,Ls-dyna,Ansys等软件的应力应变形式"""
    match target:
        case 'abq-sta':
            # Abaqus/Standard应力应变形式
            t=np.array([[1,0,0,0,0,0],
                        [0,1,0,0,0,0],
                        [0,0,1,0,0,0],
                        [0,0,0,0,0,1],
                        [0,0,0,0,1,0],
                        [0,0,0,1,0,0]],dtype=float)
        case 'ls-dyna':
            # Ls-dyna应力应变形式
            t=np.array([[1,0,0,0,0,0],
                        [0,1,0,0,0,0],
                        [0,0,1,0,0,0],
                        [0,0,0,0,0,1],
                        [0,0,0,1,0,0],
                        [0,0,0,0,1,0]],dtype=float)
        case 'ansys':
            # Ansys应力应变形式
            t=np.array([[1,0,0,0,0,0],
                        [0,1,0,0,0,0],
                        [0,0,1,0,0,0],
                        [0,0,0,0,0,1],
                        [0,0,0,1,0,0],
                        [0,0,0,0,1,0]],dtype=float)
        case 'abq-exp':
            # Abaqus/Explicit应力应变形式
            t=np.array([[1,0,0,0,0,0],
                        [0,1,0,0,0,0],
                        [0,0,1,0,0,0],
                        [0,0,0,0,0,1],
                        [0,0,0,1,0,0],
                        [0,0,0,0,1,0]],dtype=float)
        case _:
            raise ValueError("target参数错误")
    return t

def StiffnessFormatTransform(C:np.ndarray,
            target:str='abq-sta',
            source:str='voigt')->np.ndarray:
    """将标准刚度矩阵C转换为ABAQUS格式的刚度矩阵

    input:

    C: (6,6) np.ndarray, 标准刚度矩阵

    target: str, 目标格式,可选值'abq-sta'(Abaqus/Standard), 'ls-dyna'(Ls-dyna), 'ansys'(Ansys), 'abq-exp'(Abaqus/Explicit)

    source: str, 源格式,可选值'voigt'(Voigt格式)

    output:

    C_target: (6,6) np.ndarray, 目标格式的刚度矩阵

    """
    t=tMatrix(target)
    if source=='voigt':
        return t.T.dot(C).dot(t)
    else:
        assert True, f"从{source}到{target}的转换尚未实现"

def StressFormatTransform(S:np.ndarray,
            target:str='abq-sta',
            source:str='voigt')->np.ndarray:
    """将标准应力向量S={sigma11,sigma22,sigma33,tau23,tau13,tau12}^T转换为target格式的应力向量"""
    t=tMatrix(target)
    if source=='voigt':
        return t.dot(S)
    else:
        assert True, f"从{source}到{target}的转换尚未实现"

def StrainFormatTransform(E:np.ndarray,
            target:str='abq-sta',
            source:str='voigt')->np.ndarray:
    """将标准应变矩阵E={eps11,eps22,eps33,gamma23,gamma13,gamma12}^T转换为target格式的应变矩阵"""
    t=tMatrix(target)
    if source=='voigt':
        return t.T.dot(E).dot(t)
    else:
        assert True, f"从{source}到{target}的转换尚未实现"

实现了不同notation格式(应力,应变,刚度矩阵)之间的转换,可以根据需要选择使用.