【MATLAB习题】四杆机构的运动学参数求解
1.问题描述

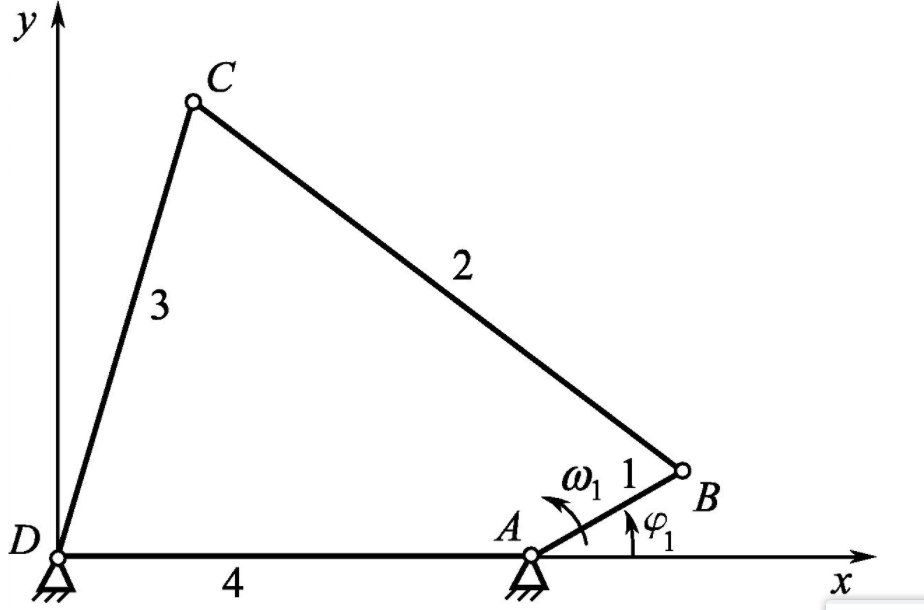
2. 推导过程



3. matlab代码
最新版代码
直接采用求微分的方式得到角度,角速度等数值解,速度慢,但是代码少,容易看懂(矩阵看起来真难受)。
以前做的一个博客文章用的是矩阵运算求解出线性方程组的方案,速度快,就是代码多一些。
%**********求解四杆机构的运动学参数***************
%1. 固定参数
l1=100 ;%单位:mm
l2=300;
l3=250;
l4=200;
w1=10.17;% rad/s
%定义角度单位换算
hd=pi/180;
jd=180/pi;
% 定义符号变量和有关的函数
syms lbd psi1
lbd(psi1)=sqrt(l4*l4+l1*l1-2*l4*l1*cos(pi-psi1));
syms theta1 theta2
theta1(psi1)= acos((l3*l3+lbd(psi1)*lbd(psi1)-l2*l2)/(2*l3*lbd(psi1)));
theta2(psi1)=asin((l1*sin(pi-psi1))/lbd(psi1));
%以上得到的结果均为弧度制
% psi3(psi1)=theta1+theta2;
% w3(psi1)=diff(psi3,psi1)*w1;
w3(psi1)=(diff(theta1,psi1)+diff(theta2,psi1))*w1;
i=1;
psi_1=zeros(1,73);
psi3=zeros(1,73);
w_3=zeros(1,73);
%循环求值
for n=0:5:360
%sin ,cos 函数是弧度制单位
psi_1(i)= n;
psi1=n*hd;
psi3(i)=theta1(psi1)+theta2(psi1);
w_3(i)=w3(psi1); %unit:rad/s
psi3(i)=psi3(i)*jd; %psi3转为角度制
i=i+1;
end
subplot(2,2,1);
plot(psi_1(:,1:73),psi3(:,1:73),'-b');
title('杆3的角度随\psi_1的变化曲线')
xlim([0 360])
xlabel('\psi_1 /\circ')
ylabel('\psi_3 / \circ')
grid on;
subplot(2,2,2);
plot(psi_1(:,1:73),w_3(:,1:73),'-r')
title('杆3的角速度曲线');
xlabel('角度')
xlim([0 360])
ylabel('角速度/rad\cdots^{-1}')
grid on;
subplot(2,2,[3 4])
[ax,h1,h2]=plotyy(psi_1,psi3,psi_1,w_3);
% 设置label
d1=get(ax(1),'ylabel');%取出左侧轴的ylabel句柄
set(d1,'string','角度值');%设置ylabel的值
d2=get(ax(2),'ylabel');%取出右侧轴的ylabel句柄
set(d2,'string','速度值');%设置ylabel的值
% 设置图例
legend([h1,h2],'角度','角速度');
%设置坐标轴刻度,范围
set(ax,'Xlim',[0 360],'xtick',[0:10:360])
history version
%**********求解四杆机构的运动学参数***************
%1. 固定参数
l1=100 ;%单位:mm
l2=300;
l3=250;
l4=200;
w1=10.17;% rad/s
%定义角度单位换算
hd=pi/180;
jd=180/pi;
% 定义符号变量和有关的函数
syms lbd psi1
lbd(psi1)=sqrt(l4*l4+l1*l1-2*l4*l1*cos(pi-psi1));
syms theta1 theta2
theta1(psi1)= acos((l3*l3+lbd(psi1)*lbd(psi1)-l2*l2)/(2*l3*lbd(psi1)));
theta2(psi1)=asin((l1*sin(pi-psi1))/lbd(psi1));
%以上得到的结果均为弧度制
i=1;
psi_1=zeros(1,74);
psi3=zeros(1,74);
psi2=zeros(1,74);
%循环求值
for n=0:5:360
%sin ,cos 函数是弧度制单位
psi_1(i)= n;
psi1=n*hd;
psi3(i)=theta1(psi1)+theta2(psi1);
psi2(i)=asin((l3*sin(psi3(i))-l1*sin(psi1))/l2);
psi2(i)=psi2(i)*jd; %弧度制转角度制
psi3(i)=psi3(i)*jd;
i=i+1;
end
plot(psi_1(:,1:73),psi3(:,1:73),'-b');
title('\psi_3')
xlim([0 360])
xlabel('\psi_1 /\circle')
ylabel('\psi_1&\psi-2 /\circ')
ylim([-360 360])
grid on;
hold on;
plot(psi_1(:,1:73),psi2(:,1:73),'-.r');
结果-速度图&角位移图
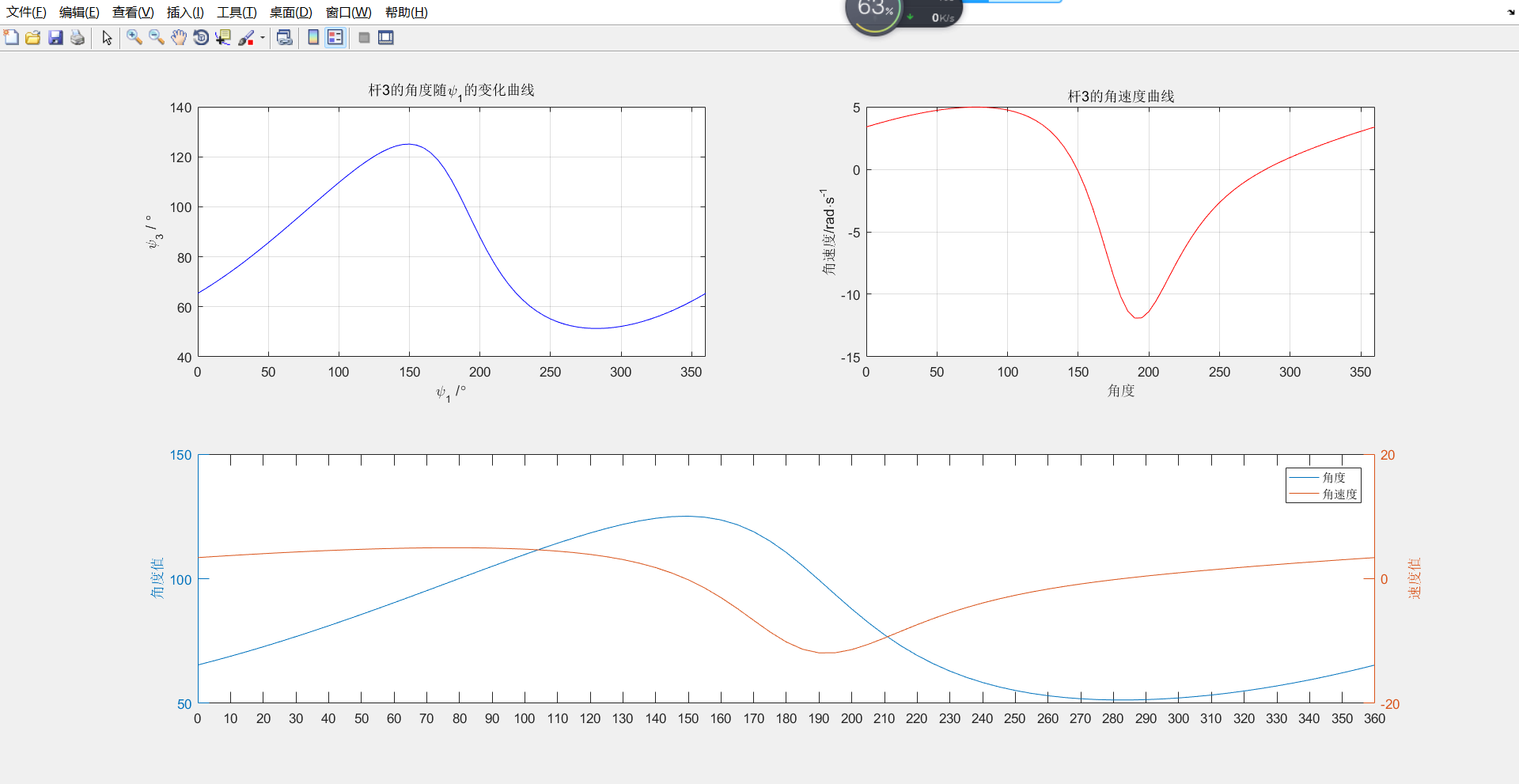
【MATLAB习题】四杆机构的运动学参数求解的更多相关文章
- opencv通过dll调用matlab函数,图片作为参数
[blog 项目实战派]opencv通过dll调用matlab函数,图片作为参数 前文介绍了如何“csharp通过dll调用opencv函数,图片作为参数”.而在实 ...
- flink 批量梯度下降算法线性回归参数求解(Linear Regression with BGD(batch gradient descent) )
1.线性回归 假设线性函数如下: 假设我们有10个样本x1,y1),(x2,y2).....(x10,y10),求解目标就是根据多个样本求解theta0和theta1的最优值. 什么样的θ最好的呢?最 ...
- 机器学习(二):感知机+svm习题 感知机手工推导参数更新 svm手推求解二维坐标超平面直线方程
作业1: 输入: 训练数据集 \(T = {(x1; y1); (x2; y2),..., (xN; yN)}\) 其中,\(x \in R^n\), \(y \in Y = \{+1, -1\}\) ...
- 【matlab】设定函数默认参数
C++/java/python系列的语言,函数可以有默认值,通常类似如下的形式: funtion_name (param1, param2=default_value, ...) 到了matlab下发 ...
- matlab 中“newff” 函数的参数设置
matlab 中"newff" 函数的使用方法技巧|和各参数的意义 先来一个简单的源程序让大家练习一下: % Here input P and targets T define a ...
- Matlab中 awgn 函数输入参数带有‘measured’ 时snr的含义
MATLAB中awgn 函数可以为输入信号x 添加一定大小的噪声. out = awgn(in,snr,'measured'); 是一种常见的使用方法,意思是在添加噪声前先测量一下输入信号的功率,再 ...
- matlab中nargin函数输入参数数目
来源:https://ww2.mathworks.cn/help/matlab/ref/nargin.html?searchHighlight=nargin&s_tid=doc_srchtit ...
- Matlab摄像头标定得出的参数保存为xml
最近在做双摄像头的立体匹配,发现OpenCV定标效果不如MatLab的效果,于是用MatLab标定箱做标定,将得到的结果保存为xml,然后,提供给opencv使用.MatLab标定箱做标定得到的结果如 ...
- C# 二元一次方程参数求解
本文记录了关于求直线斜率及纵截距值的简单方法,只是简单的记录下求解思路,最终还需根据具体项目进行优化. 设直线方程式为:y=kx+b 编程思想: 1.代入y1与x1的值,得到:y1=kx1+b 2.代 ...
- MATLAB学习(四)线性方程求解,多项式运算,函数局部最优解
>> A=[2 1 3;1 3 2];B=[5;10] B = 5 10 >> X=lsqnonneg(A,B) X = 0 2.8571 0.7143 >> A\ ...
随机推荐
- kubernetes批量删除长期处于Terminating状态的namespace
环境是k3s 1.19.1版本 有时候跑实验,实验总是卡住,而且还删不了ns,一跑又n个 强行删除有风险,强删需谨慎!! 创建脚本 delns.sh #!/bin/bash for i in &quo ...
- Qt音视频开发48-通用通道管理
一.前言 把通用的视频控件搞定以后,后期增加新的内核方便多了,不需要在好多个文件复制粘贴之类的,接下来就是需要一个统一的类来管理视频监控系统中的16个通道或者32个通道,甚至64个通道也有可能,当然, ...
- [转]基于GMap.Net的地图解决方案
一 地图的加载与显示 关于GMap的介绍与使用可以看我以前的文章: GMap.Net开发之在WinForm和WPF中使用GMap.Net地图插件 GMap.Net是.Net下一个地图控件,可以基于Ht ...
- 网页端IM通信技术快速入门:短轮询、长轮询、SSE、WebSocket
本文来自"糊糊糊糊糊了"的分享,原题<实时消息推送整理>,有优化和改动. 1.写在前面 对Web端即时通讯技术熟悉的开发者来说,我们回顾网页端IM的底层通信技术,从短轮 ...
- Optional的使用与解析
引言 今天在项目中看到了大量Optional的使用,之前我也了解过Optional,是Java8中的新特性,并且便利地为空指针问题提供了处理方法,可以避免繁琐的if/else. 但是并没有真正在项目中 ...
- 【Windows】终端配置代理
Windows cmd 设置代理 设置 HTTP 代理: set http_proxy=http://127.0.0.1:7890 & set https_proxy=http://127.0 ...
- docker和主机之间文件传输
docker和主机之间文件传输 1.从docker内部向主机传输文件 语法: docker cp [OPTIONS] CONTAINER:SRC_PATH DEST_PATH|- 示例:将容器96f7 ...
- c# 反射私有类和私有方法
namespace ClassLibrary1 { class InnerClass//私类 { public string Test(string s) { return "" ...
- nginx详细参数配置(史上最全)
Nginx (engine x) 是一个轻量级高性能的HTTP和反向代理服务器,同时也是一个通用 代理服务器 (TCP/UDP/IMAP/POP3/SMTP),最初由俄罗斯人Igor Sysoev编写 ...
- 项目PMP之五项目范围管理
项目PMP之五--项目范围管理 一.定义:确保项目做且只做所需的工作:范围包括产品范围(特性和功能)和项目范围(交付产品所需完成的工作) 适应型生命周期:相关方持续参与,应对大量变更(敏捷),实时 ...
