点击下方 veiw code 查看完整代码

18438 First Blood

题意：\(\sum_{i=1}^a\)\(\sum_{j=1}^b\)(i+j) ， 求和。

思路：签到题，照着题目A就行了。

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 3e4+2;

const int inf=0x3f3f3f3f;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

int main()

{

    int kase;

    cin>>kase;

    while(kase--)

    {

        ll a,b; cin>>a>>b;

        ll ans = 0;

        rep(i,1,a) rep(j,1,b) ans += i+j;

        cout<<ans<<endl;

    }

    return 0;

}

18429 Earning Money for Dating

题意：有两个工作，每个工作需要耗时一小时，都需要做m次，同时每个工作有冷却时间,CD分别是t\({_0}\)和t\({_1}\)。问最小需要多长时间才能把两件工作做完（各m次）。

1.想要天数尽量少，那就尽量让CD长的在等待的时候把另一个工作完成尽量多一点。

2.不妨设t\({_0}\) > t\({_1}\)。 则t\({_0}\)-1就是我们要来填充的间隙，-1是因为Job0工作就要1个小时。

现在，如果t\({_0}\)-1的时间内能让Job1完成当前的，同时开始下一次，那么最长时间只取决于Job0（脑补一下为什么），此时的答案就是t\({_0}\) * (m-1)+1。m-1是因为只有前m-1次需要等待，最后一次直接用1小时完成。如m=2, t\({_0}\) = 5 , t\({_1}\) = 3时 ， 一次t\({_0}\)-1的间隔里面可以让Job1完成一轮工作加休息同时开始新的一次(5-1 = 3+1) ，所以答案是5 * 1 + 1 = 6。如下图：

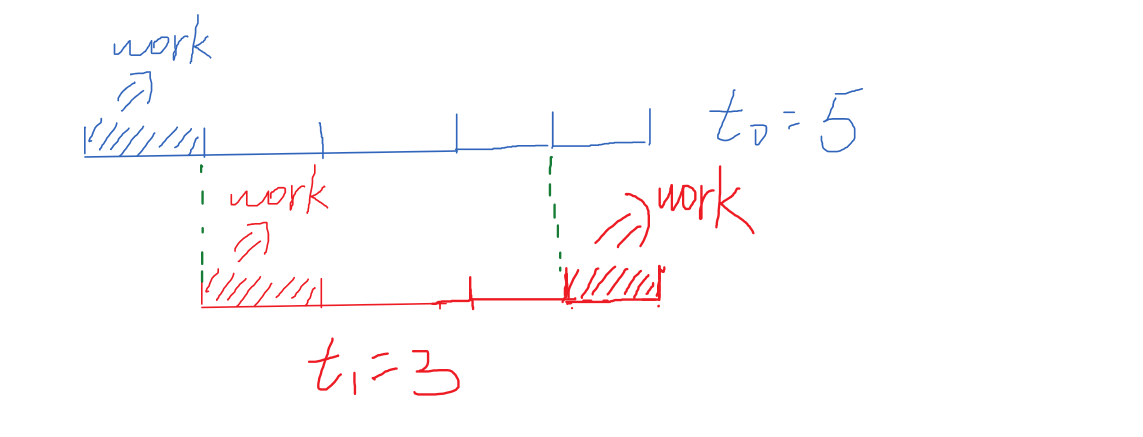
但是当t\({_0}\) - t\({_1}\) <= 1的时候，Job1在t\({_0}\)-1间隙里完成一轮工作加休息后想开始新工作时会和Job0冲突。什么意思？ 如t\({_0}\) = 5, t\({_1}\) = 4， Job1在t\({_0}\)-1完成一轮，这个时候Job1和Job0开始工作的时刻重合了。这样就需要在上面讨论的结果里多加一个1，即t\({_0}\)*(m-1)+1 +1 。如下图：



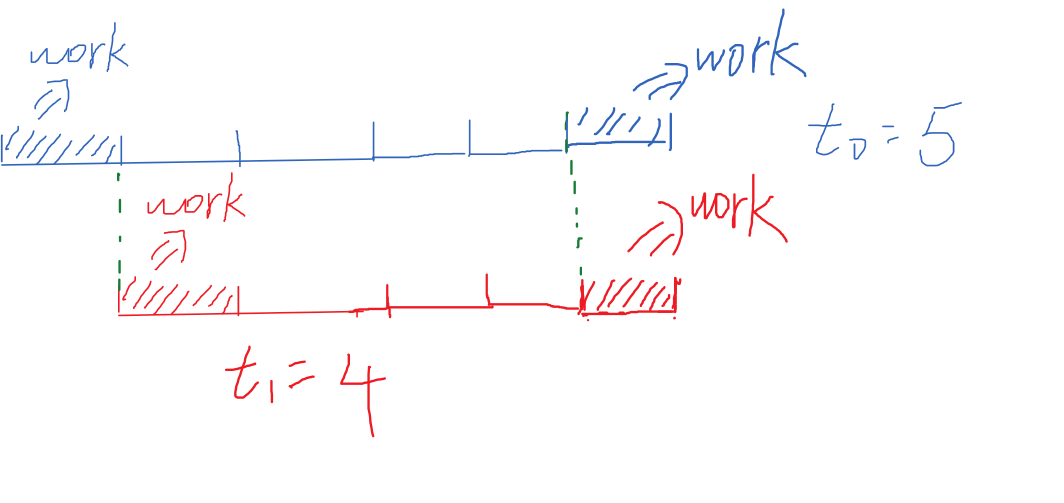
3.最后讨论一下t1和t0同时为1的情况，这个时候是直接2m。

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 1e6+200;

const int inf=0x3f3f3f3f;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

int main()

{

    ll kase;

    cin>>kase;

    while(kase--)

    {

        ll m;

        cin>>m;

        ll t0, t1; cin>>t0>>t1;

        if(t0==0) t0 = 1; if(t1==0) t1 = 1;

        if(t0<t1) swap(t0,t1);

        if(m==1)

        {

            cout<<2<<endl;

            continue;

        }

        if(t0==1&&t1==1)        //都为1就只能2m

        cout<<2*m<<endl;

        else        //开始时刻冲突就多+1

        {

            if(t0-t1<=1) cout<<t0*(m-1) + 2<<endl;

            else cout<<t0*(m-1) + 1<<endl;

        }

    }

    return 0;

}

18430 Aerial Photography

题意：有n个点，从原点出发，每次可以最多走M个单位距离，不够的时候又可以回原点重新获得M次单位的距离（返航也要消耗M），问最少返航多少次可以走完n个点。

数据量小，直接暴力。(138ms AC)

1.先预处理一下坐标。给n个点两两建边。

2.dfs枚举每个点，当前这个点无非有两种走法，一种是飞到一个除自身和原点以外的点、一个是飞回原点补充能量

3.那么，针对上述两种情况，我要使得每个点都有这两种选择，那就必须到的每个点都有“退路”，就是你到这个点的时候要保证还有能量回原点苟。即判断条件是当前剩余Left - D[x][y] - D[y][0] >=0 ，表示当前剩余的能量够飞到y点且y点还能飞回原点。

4.然后什么时候要飞回原点呢？你要是能量够的话，完全没必要回去。为什么？你如果能量够回原点一趟再去别的点y，那为什么不直接飞去点y呢？所以只有当没有点可以飞的时候才要回原点

5.然后递归出口就是飞满了n个点。最后肯定是停在第n个点的。而我们的条件限制又使得每次可以够能量回原点。所以最后走完n个点就直接可以 ans = min(ans.cur)了。

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 3e4+2;

const ll inf= 1e18;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

typedef struct Pos

{

    ll x;

    ll y;

} P;

P a[150];

ll vis[150];

ll n,m;

double D[50][50];

ll ans = inf;

ll cur = 1;

void dfs(ll x, double Left, ll num)

{

    if(cur>ans) return;

    if(num==n)

    {

        ans = min(cur,ans);

        return;

    }

    bool flag = false;

    for(int i=0;i<=n; ++i)

    {

        ll v = i;  double cost = D[x][i];

        if(vis[v]||v==0||v==x) continue;

        if(Left-cost-D[v][0]>=0)

        {

            flag = true;

            vis[x] = 1;

            dfs(v,Left-cost,num+1);

            vis[x] = 0;

        }

    }

    if(!flag)

    {

        cur++;

        vis[x] = 1;

        dfs(0,m,num);

        cur--;

        vis[x] = 0;

    }

}

int main()

{

    ll kase;

    kase = read();

    while(kase--)

    {

        mem(vis,0);  ans = inf; cur = 1;

        n = read(); m = read(); mem(D,0);

        if(n==0)

        {

            cout<<0<<'\n';

            continue;

        }

        rep(i,1,n) a[i].x = read(), a[i].y = read();

        a[0].x = a[0].y = 0;

        rep(i,1,n) rep(j,0,i-1)

        {

            double dis =sqrt ( (a[i].x-a[j].x)*(a[i].x-a[j].x) + (a[i].y-a[j].y)*(a[i].y-a[j].y) );

            D[i][j] = D[j][i] = dis;

        }

        dfs(0LL,m,0);

        cout<<ans<<endl;

    }

    return 0;

}

18434 Painting Walls

题意：题意：给一个序列若干询问，每次询问对m个区间计数+1，求最后计数等于k的区间元素和。

思路：差分和哈希

1.首先发现，题目简化后的逻辑表达就是每次询问让你给区间【L,R】内的值+1，然后每次询问完回答该操作完后有哪些区间被覆盖了k次，输出对应区间和

2.对于区间加和问题，可能会往线段树或者树状数组的方向想，但是这个题明确是每次+1，就相当于区间的计数，所以可以往差分的方向想。

3.构建差分数组b[i] = a[i] - a[i-1]，它有什么特点呢？一个是差分数组的i位置前缀和就是对应a[i]（自行证明），另一个就是本题关键——我要让【L,R】区间内的值+1，只需要b[L]++, b[R+1]--即可。（为什么？就相当于这个区间内部差分不变，因为是同时+1。而对于区间左边界相当于比前一个数多了一，右边界比后一个数少1）。

4.然后，用map存这些区间端点（自带按照键大小排序），这个时候我们只需要遍历一遍这些询问到的端点，用变量cur += b[i]，表示当前区间的询问次数。

比如：询问【1,10】，【3,5】。通过上述知道

b[1] = 1 , b[3] = 1 , b[6] = -1, b[11] = -1,

假设本次询问 k=2 . 那么在遍历一遍询问到的区间端点时,

1).cur += b[1] => 1

2).cur += b[3] => 2 注意，此时cur等于k，说明这个点开始的区间已经满足题意了。但我们现在不知道这个区间多长，就先标记着 flag = 1

3).cur += b[6] => 1 哦吼，发现cur变了，这个时候我们就知道前面满足题意的区间是多长了，就是i - pre（前一个端点）+ 1 。这个时候答案就是ans += sum[i-1] - sum[pre-1]。同时flag=0

4).cur += b[11] => 0 发现没啥玩意了。不计数。

5.主体思路便是如上。最后注意一个非常恶心的点。k可以取0，这个时候要反过来求！

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 1e6+200;

const int inf=0x3f3f3f3f;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

ll b[maxn];

ll a[maxn];

ll sum[maxn];

map<ll,ll> Map;

int main()

{

   // freopen("DATA.txt","r",stdin);

    ll kase;

    kase = read();

    while(kase--)

    {

        ll n,d;

        n = read(); d = read(); rep(i,0,n) sum[i] = 0;

        rep(i,1,n) a[i] = read(), sum[i] = sum[i-1] + a[i];

        rep(i,1,d)

        {

            Map.clear();

            ll m, k;

            m = read(); k = read();

            if(k)

            {

                 rep(j,1,m)

                {

                    ll L, R;

                    L = read(); R = read();

                    b[L] ++ , b[R+1] --;

                    Map[L] = Map[R+1] = 1;

                }

                ll cur = 0; ll pre = 1; ll ans = 0; bool flag = 0;

                for(map<ll,ll>:: iterator it = Map.begin(); it!=Map.end();it++)

                {

                    cur += b[it->fi];

                    if(flag) ans += sum[it->fi-1] - sum[pre-1];

                    if(cur==k)

                    flag = 1;

                    else flag = 0;

                    pre = it->fi;

                }

                printf("%lld\n",ans);

                for(map<ll,ll>:: iterator it = Map.begin(); it!=Map.end();it++) b[it->fi] = 0;

            }

            else

            {

                    rep(j,1,m)

                {

                    ll L, R;

                    L = read(); R = read();

                    b[L] ++ , b[R+1] --;

                    Map[L] = Map[R+1] = 1;

                }

                ll cur = 0; ll pre = 1; ll ans = 0; bool flag = 0;

                for(map<ll,ll>:: iterator it = Map.begin(); it!=Map.end();it++)

                {

                    cur += b[it->fi];

                    if(flag) ans += sum[it->fi-1] - sum[pre-1];

                    if(cur)

                    flag = 1;

                    else flag = 0;

                    pre = it->fi;

                }

                ans = sum[n] - sum[0] - ans;

                printf("%lld\n",ans);

                for(map<ll,ll>:: iterator it = Map.begin(); it!=Map.end();it++) b[it->fi] = 0;

            }

        }

    }

    return 0;

}

18435 This is Not Bug, But Feature

题意：给一个字符串，若出现“bug”子串的次数超过1次，就把多出来的替换成“feature”。

小模拟题，flag标记是否为第一次出现。多出来的部分替换即可。可以用string容器简化步骤，详见代码。

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 3e4+2;

const int inf=0x3f3f3f3f;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline ll read(){ ll f = 1; ll x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

string s;

char nxt[3] = {'b', 'u', 'g' };

bool check(int pos)

{

    char cur = 0;

    for(int i=pos;i<min(s.size(), pos+3);i++)

    {

        if(cur==3) return true;

        if(nxt[cur]==s[i])

        cur++;

        else return false;

    }

    if(cur==3) return true;

    return false;

}

int main()

{

    int kase = 10;

    while(kase--)

    {

        getline(cin,s); int flag = 0;

        for(int i=0;i<s.size();i++)

        {

            if(check(i))

            {

                if(!flag)

                flag = 1;

                else

                {

                    string t1(s,0,i);

                    string t2(s,i+3,s.size()-i-2);

                    string t3 = "feature";

                    t1 = t1+t3;

                    t1 = t1 + t2;

                    s = t1;

                    i += 6;

                }

            }

        }

        cout<<s<<endl;

    }

    return 0;

}

18436 Path

题意：给一个图。每条边有两个权值A,B。问1->n的路径中\({SumA\over SumB}\)的最小值。

这个题有一点技巧性。。。

思路如下：

1.首先，如果往最短路的方向想的话可以收收了，不然会和我一样前期陷进死胡同。

2.我们发现，这个题要求SumA/SumB最小，而不是求路径和最小，这说明了什么？我们可以重复走一条边任意多次！

有什么用呢？比如我们发现有两点之间的SumA/SumB是整个图里面最小的（而且在1->n路径上），那么我们就可以把这两点的之间的边来回走无限多次。

这样的效果是什么，取极限来看，这样整个的和就无限接近于 (ksumA)/(ksumB) = sumA/sumB。其中k->正无穷。这样，问题就变成了，只要我找到两点之间的suma/sumb是最小的，通过走这个路径无限次，答案就一定会取到它。比如1->2->3的路径，n=3时，若1->2的A/B是1/2,而2->3的A/B是1/10，那我们就把2->3这条边反复横条无限多次，这样前面那个1/2就可以忽略不计，答案既然是1/10。

3.第二步仔细理解一下。然后我们就来到第三个问题，这两个点怎么找呢？

我先说结论，最小值肯定是在相邻的两个点中产生的。

比如1->2->3->4->5，我们要找的两个点的不会找13之间或者14之间或者24之间这样的。为什么？

其实是个数学问题，假设\({A1\over B1}\) < \({A2\over B2}\) , 那么一定有\({A1+A2\over B1+B2}\)> \({A1\over B1}\) ，最小值还是A1/B1所在的那条边（证明的话两个不等式各自交叉相乘一下会发现是一样的）。所以，最小值一定在相邻的点中产生。

4.那问题越来越简单了，我们只需要找到最A/B最小的一条边即可。但是最后有一点要注意除了结点1和结点n是保证联通的，其他点不一定和1->n的路径上的点联通。所以这里要用一个并查集维护一下。一条边上的两个点同时和1和n联通才能选。

5.最后求最简式只需要上下除个最大公约数即可。

view code 
#include<iostream>

#include<string>

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<map>

#include <queue>

#include<sstream>

#include <stack>

#include <set>

#include <bitset>

#include<vector>

#define FAST ios::sync_with_stdio(false)

#define abs(a) ((a)>=0?(a):-(a))

#define sz(x) ((int)(x).size())

#define all(x) (x).begin(),(x).end()

#define mem(a,b) memset(a,b,sizeof(a))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define rep(i,a,n) for(int i=a;i<=n;++i)

#define per(i,n,a) for(int i=n;i>=a;--i)

#define pb push_back

#define mp make_pair

#define fi first

#define se second

using namespace std;

typedef long long ll;

typedef pair<ll,ll> PII;

const int maxn = 4e4+200;

const int inf=0x3f3f3f3f;

const double eps = 1e-7;

const double pi=acos(-1.0);

const int mod = 1e9+7;

inline int lowbit(int x){return x&(-x);}

int gcd(int a,int b){return b?gcd(b,a%b):a;}

void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);

inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}

inline ll inv(ll x,ll p){return qpow(x,p-2,p);}

inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}

inline int read(){ int f = 1; int x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }

int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

const int V = 5005, E = 55500;

int head[V], nxt[E], pnt[E], e = 1;

double costa[E], costb[E];

int Map[maxn];

int fa[maxn];

int n,m;

void addedge(int x, int y, int A, int B)

{

    pnt[e] = y;

    costa[e] = (double)A;

    costb[e] = (double)B;

    nxt[e] = head[x];

    head[x] = e++;

}

int get(int x)

{

    if(fa[x]==x) return x;

    return fa[x] = get(fa[x]);

}

void merge(int x, int y)

{

    int fx = get(x);

    int fy = get(y);

    if(fx!=fy) fa[fx] = fa[fy];

}

void init()

{

    rep(i,0,n+1) fa[i] = i,head[i] = 0;

    e = 1;

}

int main()

{

    int kase;

    cin>>kase;

    while(kase--)

    {

        n = read(), m = read();

        init();

        rep(i,1,m)

        {

            int x = read(), y = read();

            int A = read(), B = read();

            merge(x,y);

            addedge(x,y,A,B);

            addedge(y,x,A,B);

        }

        int ansA=1e12, ansB=1;

        rep(i,1,n)

        {

            for(int j=head[i]; j; j = nxt[j])

            {

                int v = pnt[j];

                if(get(v)==get(1)&&get(v)==get(n))

                {

                    if((double)ansA/ansB > costa[j]/costb[j])

                    {

                        ansA = costa[j];

                        ansB = costb[j];

                    }

                }

            }

        }

        int d = gcd(ansA,ansB);

        ansA /= d, ansB /= d;

        printf("%d/%d\n",ansA,ansB);

    }

    return 0;

}

SCAU 2019年校赛 部分题解的更多相关文章

  1. BJOI 2019 模拟赛 #2 题解

    T1 完美塔防 有一些空地,一些障碍,一些炮台,一些反射镜 障碍会挡住炮台的炮, 反射镜可以 90° 反射炮台的光线,炮台可以选择打他所在的水平一条线或者竖直一条线 求是否有一组方案满足每个空地必须要 ...

  2. SCAU 13校赛 17115 ooxx numbers

    17115 ooxx numbers 时间限制:1000MS  内存限制:65535K 题型: 编程题   语言: 无限制 Description a number A called oo numbe ...

  3. hdu6578 2019湖南省赛D题Modulo Nine 经典dp

    目录 题目 解析 AC_Code @ 题目 第一题题意是一共有{0,1,2,3}四种数字供选择,问有多少个长度为n的序列满足所有m个条件,每个条件是说区间[L,R]内必须有恰好x个不同的数字. 第二题 ...

  4. 【题解】Comet OJ 国庆欢乐赛 简要题解

    [题解]Comet OJ 国庆欢乐赛 简要题解 A 直接做 B 直接做,结论: \[ ans=\max([Max\ge \mathrm{sum}] Max,s[n]/2) \] C 考虑这样一个做法: ...

  5. 【洛谷比赛】[LnOI2019]长脖子鹿省选模拟赛 T1 题解

    今天是[LnOI2019]长脖子鹿省选模拟赛的时间,小编表示考的不怎么样,改了半天也只会改第一题,那也先呈上题解吧. T1:P5248 [LnOI2019SP]快速多项式变换(FPT) 一看这题就很手 ...

  6. 哈尔滨理工大学ACM全国邀请赛（网络同步赛）题解

    题目链接 提交连接:http://acm-software.hrbust.edu.cn/problemset.php?page=5 1470-1482 只做出来四道比较水的题目,还需要加强中等题的训练 ...

  7. 第七届ACM趣味程序设计竞赛第四场（正式赛） 题解

    Final Pan's prime numbers 题目连接: http://acm.uestc.edu.cn/#/problem/show/1272 题意 给你n,要求你在[4,n]范围内找到一个最 ...

  8. CDOJ 第七届ACM趣味程序设计竞赛第三场（正式赛） 题解

    宝贵资源 题目连接: http://acm.uestc.edu.cn/#/problem/show/1265 题意 平面上给n个点(n<=1000),要求找一个面积最小的正方形,将所有的点都囊括 ...

  9. 2016 ACM/ICPC Asia Regional Qingdao Online（2016ACM青岛网络赛部分题解）

    2016 ACM/ICPC Asia Regional Qingdao Online(部分题解) 5878---I Count Two Three http://acm.hdu.edu.cn/show ...

  10. 2019浙江省赛B zoj4101 Element Swapping(推公式)

    http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=6003 题意 \(数组a通过交换一对数字,得到了b数组,给出x=\sum^n_{ ...

随机推荐

  1. Java 21 新特性

    Java 21 是 Java 语言的一次重要更新,引入了若干新的特性,提升了开发者的编程效率和代码质量.本文将详细介绍 Java 21 的新特性,包括基础概念.使用方法.常见实践以及最佳实践. 简介 ...

  2. kettle介绍-参数变量

    ETL中为什么使用参数变量 实现ETL的复用 D,Q,P环境不同,使用变量方便发布 有的条件需要外部传入 增量ETL 灵活性强 kettle中参数变量种类 Environment Variables ...

  3. 在 .NET 中的 ConvertAll 和 Select 方法哪个性能好

    .NET 的 List 中提供了 ConvertAll 和 Select 两个方法,在开发中实际上应该使用哪一个? 接下来通过基准测试脚本来对比性能. 先编写基准测试脚本: [MemoryDiagno ...

  4. Cursor怎么使用，3分钟上手Cursor：比ChatGPT更懂需求，用聊天的方式写代码，GPT4、Claude 3.5等先进LLM辅助编程

    前言 在人工智能工具井喷的今天,大家早已习惯用AI辅助编程,但大多数工具要么停留在"问答式"交互,要么对复杂代码逻辑束手无策.而Cursor--这款专为开发者设计的AI编程工具,凭 ...

  5. 备份一个 VirtualizingWrapPanel ，支持虚拟化

    1 using System; 2 using System.Collections.Generic; 3 using System.Diagnostics; 4 using System.Linq; ...

  6. matlab 实现傅里叶变换

    实现傅里叶变换: ag = im2single(a1); a = fftshift(fft2(ag));%傅里叶变换和移位 aa = real(ifft2(ifftshift(csf.*a)));

  7. Web前端杂乱知识复习

    OSI OSI是Open System Interconnect的缩写,意为开放式系统互联.其各个层次的划分遵循下列原则: ​ (1)同一层中的各网络节点都有相同的层次结构,具有同样的功能. ​ (2 ...

  8. 代理模式-Proxy（动态代理）

    代理模式(Proxy) 一.作用 又叫"动态代理" 为其他对象提供一种代理以控制对这个对象的访问 二.结构图 三.场景1 远程代理: 也就是为一个对象在不同的地址空间提供局部代表. ...

  9. 鸿蒙NEXT开发教程：浅谈@ComponentV2装饰器

    听说今天的广州车展上有一部分人已经看到华为汽车的最后一"界",尊界超豪华大轿车,应该很快就要正式亮相,可以期待一波. 在api12之后,鸿蒙系统推出一个V2版本的状态管理装饰器,不 ...

  10. 妙妙线段树+DFS序判断子孙节点,但似乎还可以树链剖分?(CF Div3 909 G)

    G. Unusual Entertainment 原题链接:https://codeforces.com/contest/1899/problem/G 题目大意: 给定一棵树,根节点为1,给定一个\( ...