实战 PCA

简介

PCA

code

#加载数据
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head(100)
print(pd.value_counts(data.loc[:,'label']))
#定义X，y
X = data.drop(['target','label'],axis=1)#去掉最后两列
y = data.loc[:,'label']
#建立模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)#选用最近的三个点来预测新的点属于哪一类
KNN.fit(X,y)
y_predict = KNN.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)
#将数据进行标准化处理
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)
#数据可视化
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(20,5))
plt.subplot(121)
plt.hist(X.loc[:,'sepal length'],bins=100)#这里只取sepal length这一个维度
plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)#将标准化处理后的数据可视化
plt.show()
#计算均值和标准差
x1_mean = X.loc[:,'sepal length'].mean()#原数据的均值
x1_norm_mean = X_norm[:,0].mean()#处理后数据的均值
x1_sigma = X.loc[:,'sepal length'].std()#原数据的标准差
x1_norm_sigma = X_norm[:,0].std()#处理后数据的标准差
print(x1_mean,x1_sigma,x1_norm_mean,x1_norm_sigma)
#看一下原数据的维度，下面要用
print(X.shape)
# pca analysis
from sklearn.decomposition import PCA
pca = PCA(n_components=4)#原数据是维度是4，要进行同等维度的PCA处理，故n_components=4
X_pca = pca.fit_transform(X_norm)#这里已经是经过PCA处理的主成分了
#计算各维度下的主成分的方差比例
var_ratio = pca.explained_variance_ratio_
print(var_ratio)
#可视化数据
fig2 = plt.figure(figsize=(20,5))
plt.bar([1,2,3,4],var_ratio)#有4个维度，所以这里是1，2，3，4
plt.xticks([1,2,3,4],['PC1','PC2','PC3','PC4'])#给每维度的主成分的方差比例图加上名称
plt.ylabel('variance ratio of each PC')#给y轴加上名称
plt.show()
pca = PCA(n_components=2) #因为我们要把数据维度降为2，所以这里n_components=2
X_pca = pca.fit_transform(X_norm)
X_pca.shape #看一下维度，这里已经为2了
type(X_pca)#看一下类型
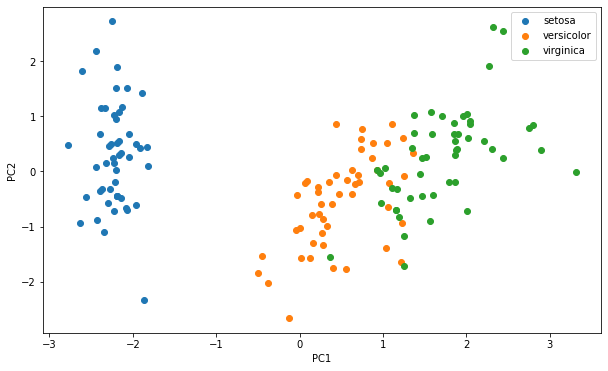
#可视化数据
fig3 = plt.figure(figsize=(10,6))
setosa = plt.scatter(X_pca[:,0][y==0],X_pca[:,1][y==0])#标签为0的
versicolor = plt.scatter(X_pca[:,0][y==1],X_pca[:,1][y==1])#标签为1的
virginica = plt.scatter(X_pca[:,0][y==2],X_pca[:,1][y==2])#标签为2的
plt.legend((setosa,versicolor,virginica),('setosa','versicolor','virginica'))
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)
y_predict = KNN.predict(X_pca)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

image