数据结构(C语言)—排序

排序

　　排序是按关键字的非递增或递减顺序对一组记录中心进行排序的操作。（将一组杂乱无章的数据按一定规律顺次排列起来。）

未定列表与不稳定列表

　　假设 K_i = K_j ( 1 ≤ i ≤ n，1 ≤ j ≤ n，i ≠ j )，在序列前尚未序列中 R_i领先于 R_j（即 i < j ）。若在排序前后的绿鬣中 R_i 仍大于 R_j ，则称所有的排序方法为稳定的，反之为不稳定。

内部排序

　　待排序记录全部存放在计算机的内存中进行排序的过程。

外部排序

　　待排序记录数量很大，以至于内存不能容纳全部数据，在排序的时候需要对外存进行访问的排序过程。

时间复杂度

　　关键字的比较次数和记录移动次数。

空间复杂度

　　执行算法所需的附加存储空间。

插入排序

直接插入排序

　　是一种简单的排序方法，基本操作是将一条记录插入到已排好序的有序列表中，从而得到一个新的、记录数量增一的有序表。

算法概述

　　(1)将序列中的第1个记录看成是一个有序的子序列;

　　(2)从第2个记录起逐个进行插入，直至整个序列变成按关键字有序序列为止；

案例

　　练习：（13，6，3，31，9，27，5，11）

　　【13】, 6, 3, 31, 9, 27, 5, 11

　　【6, 13】, 3, 31, 9, 27, 5, 11

　　【3, 6, 13】, 31, 9, 27, 5, 11

　　【3, 6, 13，31】, 9, 27, 5, 11

　　【3, 6, 9, 13，31】, 27, 5, 11

　　【3, 6, 9, 13，27, 31】, 5, 11

　　【3, 5, 6, 9, 13，27, 31】, 11

　　【3, 5, 6, 9, 11，13，27, 31】

直接插入排序算法

void InsertionSort ( SqList &L ) {

  // 对顺序表 L 作直接插入排序。

   for ( i=; i<=L.length; ++i )

       if (L.r[i].key < L.r[i-].key) {

            L.r[] = L.r[i];                 // 复制为监视哨

            for ( j=i-; L.r[].key < L.r[j].key;  -- j )

                   L.r[j+] = L.r[j];        // 记录后移

            L.r[j+] = L.r[];        // 插入到正确位置

       }

} // InsertSort

时间复杂度 O(n²)

空间复杂度 O(1)

直接插入排序是一种稳定的排序方法。

折半插入排序

　　在插入 r[i] 时，利用折半查找法寻找 r[i] 的插入位置。

折半插入排序算法

void  BInsertSort ( SqList &L )

 { for ( i = ;  i <= L.length ; ++i )

    {  L.r[] = L.r[i]; low =  ; high = i- ;

       while ( low <= high )

          {  m = ( low + high ) /  ;

             if  (  L.r[].key < L.r[m]. key  )  high = m - ;

            else  low = m + ;

           }

       for ( j=i-; j>=high+; - - j )       L.r[j+] = L.r[j];

       L.r[high+] = L.r[];

     }

  }  // BInsertSort

时间复杂度为 O(n²)

空间复杂度为 O(1)

折半插入排序是一种稳定的排序方法

希尔排序

　　实质上是采用分组插入的方法，将整个待排序记录序列分割成几组，从而减少参与直接插入排序的数据量，对每个分组分别进行直接插入排序，然后增加分组的数据量，重新分组。

技巧

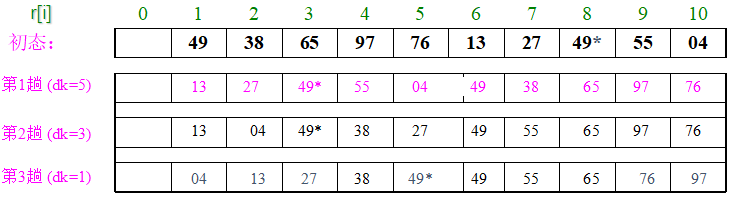
子序列的构成不是简单地“逐段分割” 将相隔某个增量dk的记录组成一个子序列让增量dk逐趟缩短（例如依次取5,3,1）直到dk＝1为止。

案例

　　关键字序列 T=(49，38，65，97, 76, 13, 27, 49*，55, 04）

希尔排序算法

void   ShellInsert(SqList &L，int dk) {

//对顺序表L进行一趟增量为dk的Shell排序，dk为步长因子

//开始将r[i] 插入有序增量子表

for(i=dk+；i<=L.length； ++ i)

      if(r[i].key < r[i-dk].key) {

       r[]=r[i]；//暂存在r[0]

       for(j=i-dk; j> &&(r[].key<r[j].key); j=j-dk)

     r[j+dk]=r[j]；//关键字较大的记录在子表中后移

        r[j+dk]=r[]；//在本趟结束时将r[i]插入到正确位置

       }

}

void   ShellSort(SqList &L，int dlta[ ]，int t){

        //按增量序列dlta[0…t-1]对顺序表L作Shell排序

   for(k=；k<t；++k)

    　ShellInsert(L，dlta[k])；

　 　//增量为dlta[k]的一趟插入排序

}  // ShellSort

时间复杂度是n和d的函数：O(n^1.25）～O(1.6n^1.25)

空间复杂度为 O(1)

希尔排序是一种不稳定的排序方法

交换排序

　　交换排序的基本思想是：两两比较待排序记录的关键字，一旦发现两个记录不满足次序要求时则进行交换，知道整个序列全部满足要求为止。

冒泡排序

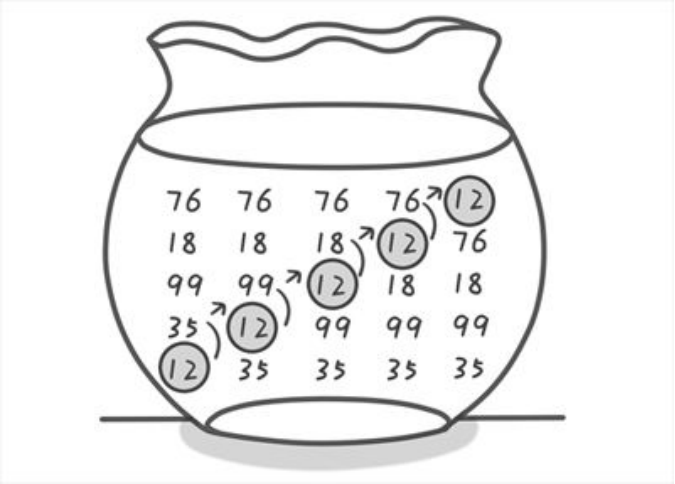
　　每趟不断将记录两两比较，并按“前小后大” 规则交换。

案例

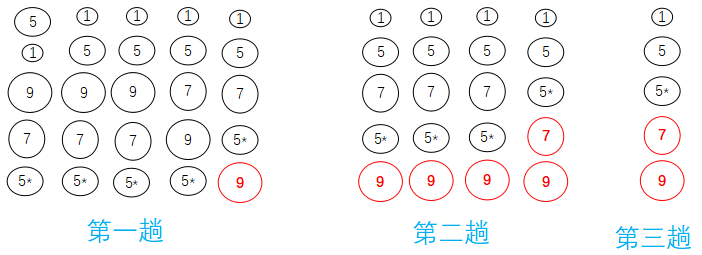
　　21，25，49， 25*，16， 08

　　21，25，25*，16， 08 ， 49

　　21，25， 16， 08 ，25*，49

　　21，16， 08 ，25， 25*，49

　　16，08 ，21， 25， 25*，49

　　08，16， 21， 25， 25*，49

冒泡排序算法

 void bubble_sort(SqList &L)

 {

    int m,i,j,flag=;   RedType x;  //flag用来标记某一列排序是否发生交换

    m=n-;

    while((m>)&&(flag==))

    {

        flag=; //置0，如果本趟排序没有发生变换，咋补执行下一趟排序

        for(j=;j<=m;j++)

        if(L.r[j].key>L.r[j+].key)

         {

             flag=; //置1，表示本趟发生了交换

             x=L.r[j];   L.r[j]=L.r[j+];   L.r[j+]=x; //交换

           }//endif

      m--;

    }//endwhile

 }

时间复杂度为 O(n²)

空间复杂度为 O(1)

冒泡排序是一种稳定的排序方法

快速排序

　　快速排序的基本思想是：从待排序记录序列中选取一个记录（通常选取第一个记录）作为“枢轴”（基准，支点)，通过一趟排序（一次划分）将待排记录分割成独立的两部分，其中一部分记录的关键字比枢轴小，另一部分记录的关键字比枢轴大。然后则可分别对这两部分记录继续进行划分，以达到整个序列有序。

案例

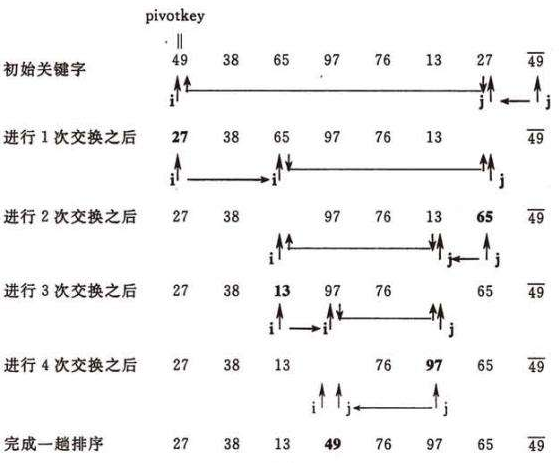
　　初始关键字 49 49* 65 97 17 27 50

　　一次交换 27 49* 65 97 17 49 50

　　二次交换 27 49* 49 97 17 65 50

　　三次交换 27 49* 17 97 49 65 50

　　四次交换 27 49* 17 49 97 65 50

快速排序算法

int Partition(SqList &L, int low, int high)

{ KeyType pivotkey;

pivotkey = L.r[low].key;

while (low<high) {

while ((low<high)&& (L.r[high].key>=pivotkey))

    --high;

    L.r[low] ←→ L.r[high];

while ((low<high)&& (L.r[low].key<=pivotkey))

     ++low;

     L.r[low] ←→ L.r[high];

   }

   return low;                                   // 返回枢轴位置

} // Partition

时间复杂度 O(nlog₂n)

空间复杂度 O(log₂n)

快速排序是一种不稳定排序。

选择排序

　　从每趟待排序的记录中选择关键字最小的记录，按顺序放在已排序的记录序列中，直到全部排完为止。

简单选择排序

基本思想

　　(1)第一次从n个关键字中选择一个最小值,确定第一个;

　　(2)第二次再从剩余元素中选择一个最小值,确定第二个;

　　(3)共需n-1次选择。

案例

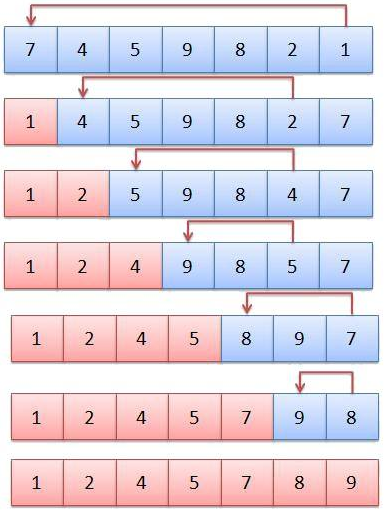
操作过程

　　设需要排序的表是A[n+1]:

　　(1)第一趟排序是在无序区A[1]到A[n]中选出最小的记录，将它与A[1]交换，确定最小值;

　　(2)第二趟排序是在A[2]到A[n]中选关键字最小的记录，将它与A[2]交换，确定次小值；

　　(3)第i趟排序是在A[i]到A[n]中选关键字最小的记录，将它与A[i]交换；

　　(4)共n-1趟排序。

简单排序算法

void  SelectSort(SqList &L)

{int i,j,low;

  for(i=;i<L.length;i++)

   {low=i;

    for(j=i+;j<=L.length;j++)

       if(L.r[j].key<L.r[low].key)

          low=j;

     if(i!=low)

       {L.r[]=L.r[i];    L.r[i]=L.r[low];      L.r[low]=L.r[];

       }

     }

}

简单选择排序方法是稳定的

时间复杂度O(n²)

空间复杂度O(1)。

树形选择排序

　　树形选择排序，又称锦标赛排序:按锦标赛的思想进行排序，目的是减少选择排序中的重复比较次数。

案例

　　　　　　　　　　　　　　　　输出 6

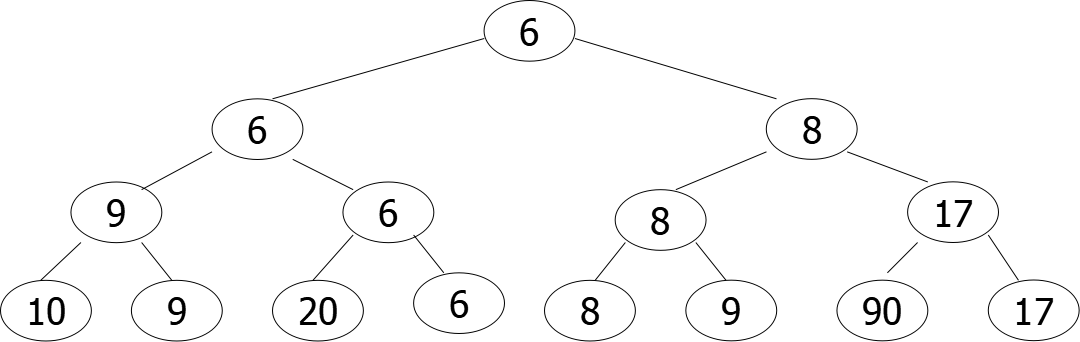
　　　　　　　　　　　　　　　　输出 8

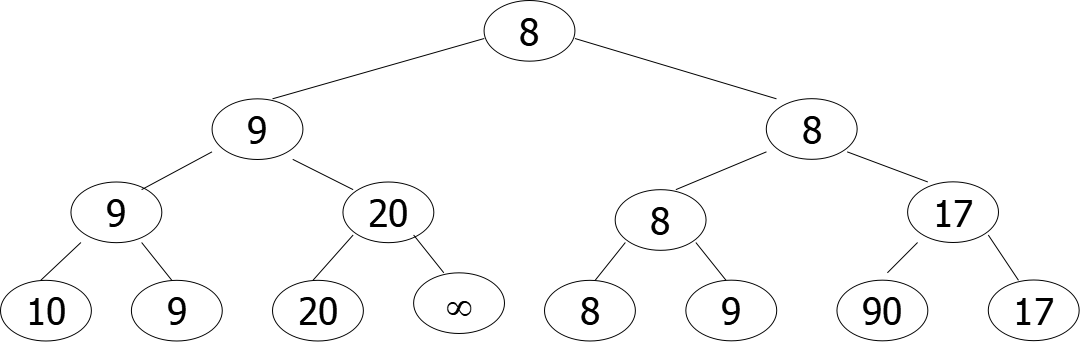
树形选择排序方法是稳定的。

时间复杂度O(nlog₂n)

空间复杂度O(n)

堆排序

n个元素的序列A[1].key,A[2].key,…,A[n].key，当且仅当满足下述关系时，称之为堆。

小根堆：A[i].key≤A[2*i].key 且 A[i].key≤A[2*i+1].

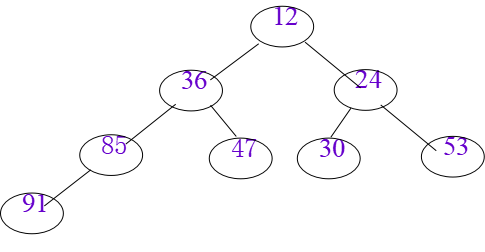
大根堆：key A[i].key≥A[2*i].key 且 A[i].key≥A[2*i+1].key

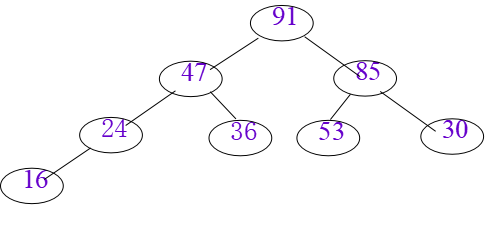
筛选算法

void HeapAdjust(HeapType &H,  int s, int m)

 {int j;

  RedType rc;

  rc = H.r[s];

  for (j=*s; j<=m; j*=)

    {if (j<m && H.r[j].key<H.r[j+].key)

       ++j;

     if (rc.key >= H.r[j].key)   break;

    H.r[s] = H.r[j];  s = j;

  }

  H.r[s] = rc;  // 插入

} // HeapAdjust

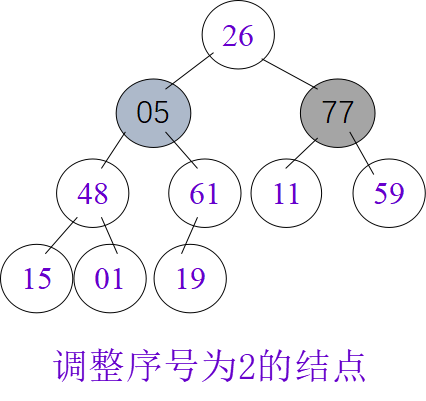
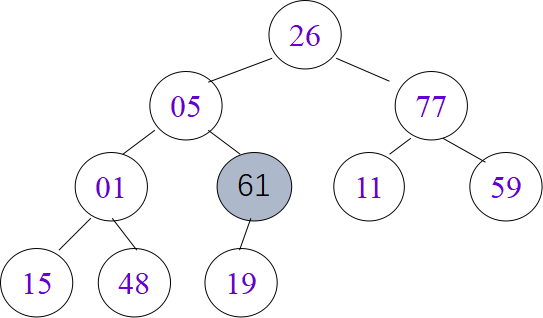
堆排序算法

void HeapSort(HeapType &H) {

   int i;

   RcdType temp;

   for (i=H.length/; i>; --i)

     HeapAdjust ( H, i, H.length );

      for (i=H.length; i>; --i) {

         temp=H.r[i];H.r[i]=H.r[];

         H.r[]=temp;

         HeapAdjust(H, , i-);

     }

} // HeapSort

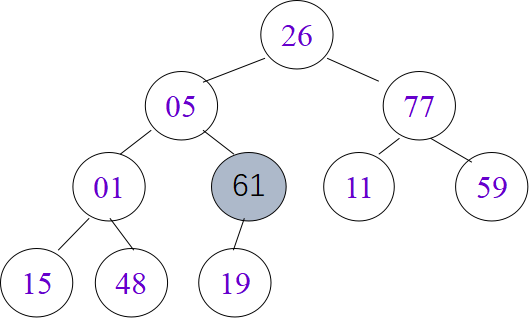
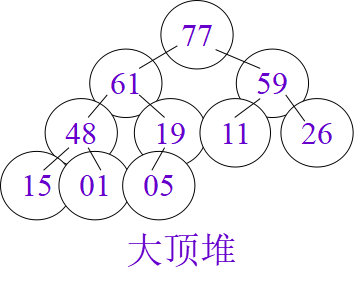
堆排序是不稳定的排序。

时间复杂度为O(nlog2n)。

最坏情况下时间复杂度为O(nlog2n)的算法。

空间复杂度为O(1)。

归并排序

　　又叫合并，两个或两个以上的有序序列合并成一个有序序列。

案例

　　初始序列为25, 57, 48, 37, 12, 82, 75, 29, 16，请用二路归并排序法排序。

算法

   for (j=m+, k=i;  i<=m && j<=n;  ++k) {

      if LQ(SR[i].key,SR[j].key) TR[k] = SR[i++];

      else TR[k] = SR[j++];

   }

   if (i<=m)

      while (k<=n && i<=m) TR[k++]=SR[i++];

   if (j<=n)

      while (k<=n &&j <=n) TR[k++]=SR[j++];

void MergeSort(RcdType A[],int n)

{int l=;

  Rcdtype B[];

  while (l<n)

  {mpass(A,B,n,l)

    l=*l;

    mpass(B,A,n,l);

    l=*l;

  }

}

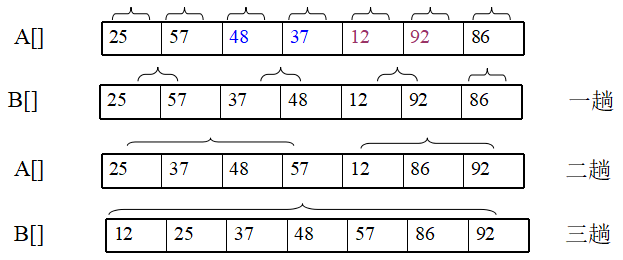
归并排序是稳定的排序方法。

时间复杂度为O(nlog₂n)

空间复杂度是O(n)

基数排序

案例

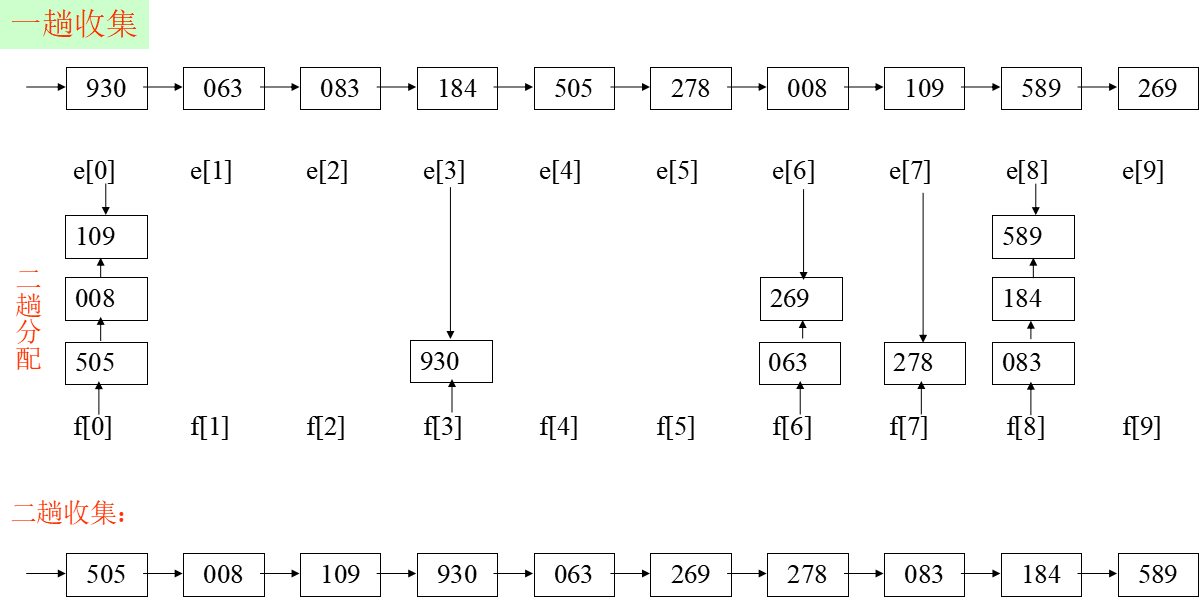
时间效率：O(d( n+rd))

空间效率：O(n+rd)

稳定性：稳定