深度学习课程笔记（三）Backpropagation 反向传播算法

深度学习课程笔记（三）Backpropagation 反向传播算法

2017.10.06 

材料来自：http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html

反向传播算法这里是用到 chain rule（链式法则）的，如下图所示：

这个应该没什么问题。大家都学过的。

我们知道总的loss 是由各个小的 loss 组合得到的，那么我们在求解 Loss 对每一个参数的微分的时候，只要对每一个 loss 都这么算就可以了。那么我们以后的例子都是以 loss 的为基础而来的。

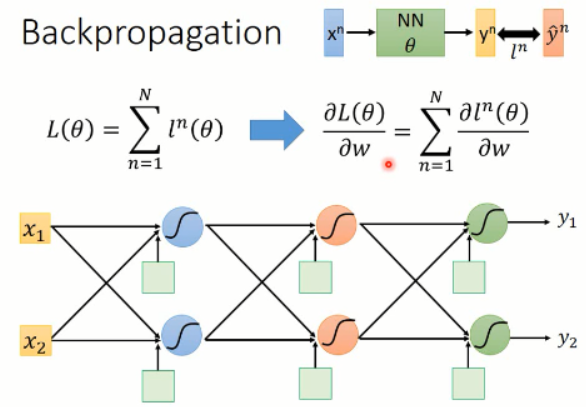
这里我们的反向传播，主要依赖于前向传播和反向传播，其loss的计算也是依赖于链式法则：

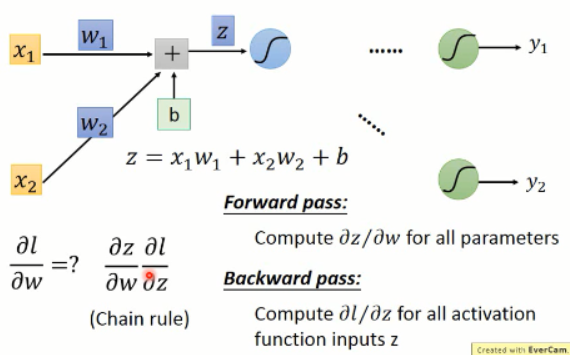
有了上面 z 的表达式，我们分别对 w1 和 w2 进行求导，我们可以得到对应的结果，分别为： x1 and x2。其实就是连接权重的输入。

那么，很直观的，我们可以得到如下的结果：

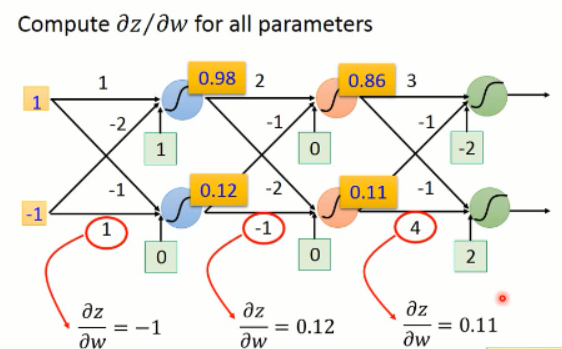
OK，现在我们求解出其中的一项了，那么，另外一项该怎么算呢？我们接着看：

这里的激活函数  a，我们用的 sigmoid，当然也可以是其他的函数了。我们对该激活函数进行求导，可以得到其微分，这个就是该项的左侧部分，那么右侧该怎么算呢？

我们知道，后面有可能又有很多的 layer，该结果可能影响后面所有的值。我们假设这里只有 2 个神经元，那么我们可以得到：

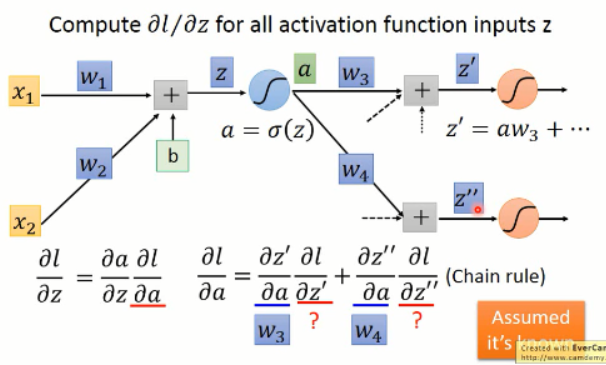
我们将右边那一项按照链式法则展开后，可以发现，又是这样子，输出对变量求导后就是输入，所以，展开后的两项的稀疏，都是已知的输入，即：w3 and w4。那么另外两项分别是什么呢？其实这个又是和后续有关的，这里我们假设这些值是已知的，那么我们就可以算出右侧的值了。

那么 l 对 z 求偏导之后的值，我们可以计算出来：

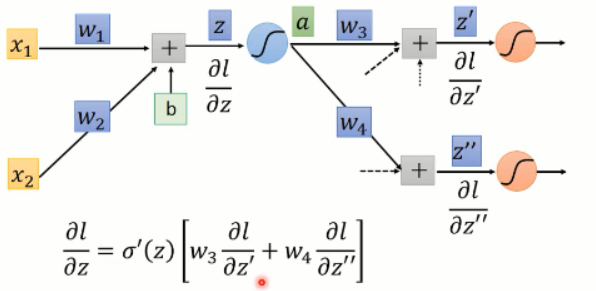
这里，其实有两种情况：

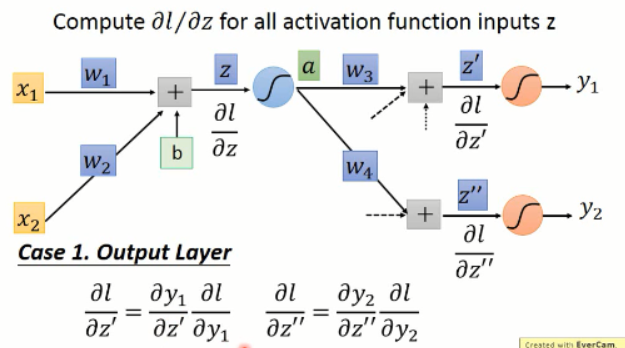
1. 此处是最后一层，那么我们就可以直接计算就行了：

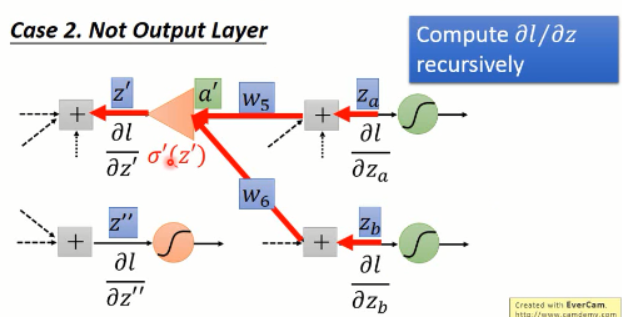
2. 若不是最后一层呢？我们只要将后面计算出的值，带入到这里就行了。

以上部分，是从输入端开始算起，所以每次都会遇到利用后面的值的问题，貌似计算量很大啊。。怎么办？

其实，没必要的啦，我们可以后面向前算，我们知道了后面的 loss，我们去求前一层的各种偏导数，然后依次向前算，就可以得到整个网络的各个偏导数的值啦。。。。

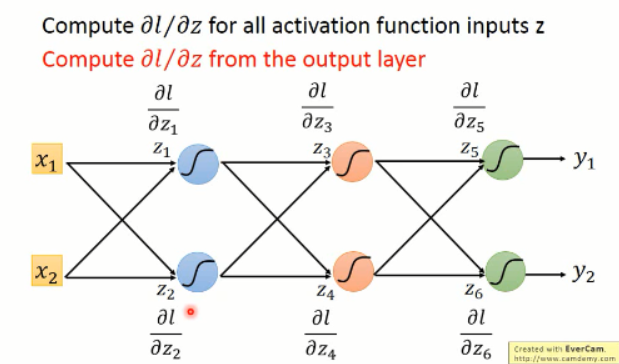
也就是说：

所以，这个过程其实就是反向传播算法啦。。。总结一下：

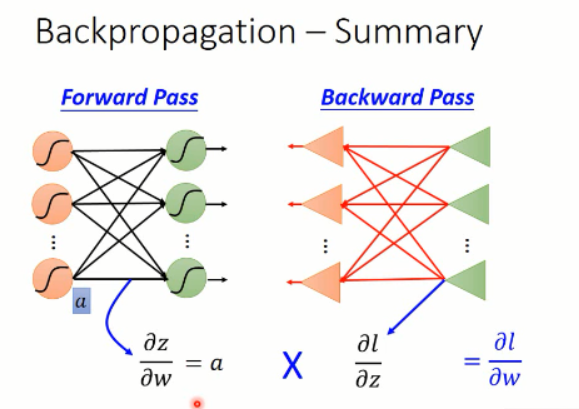
通过这样子的方法，我们得到了其偏微分，其实就是梯度啦。。。根据梯度下降的方法，我们就可以更改权重，使得 loss 最小，从而就完成了神经网络的训练。。。。