3451: Tyvj1953 Normal 点分治 FFT

国际惯例的题面: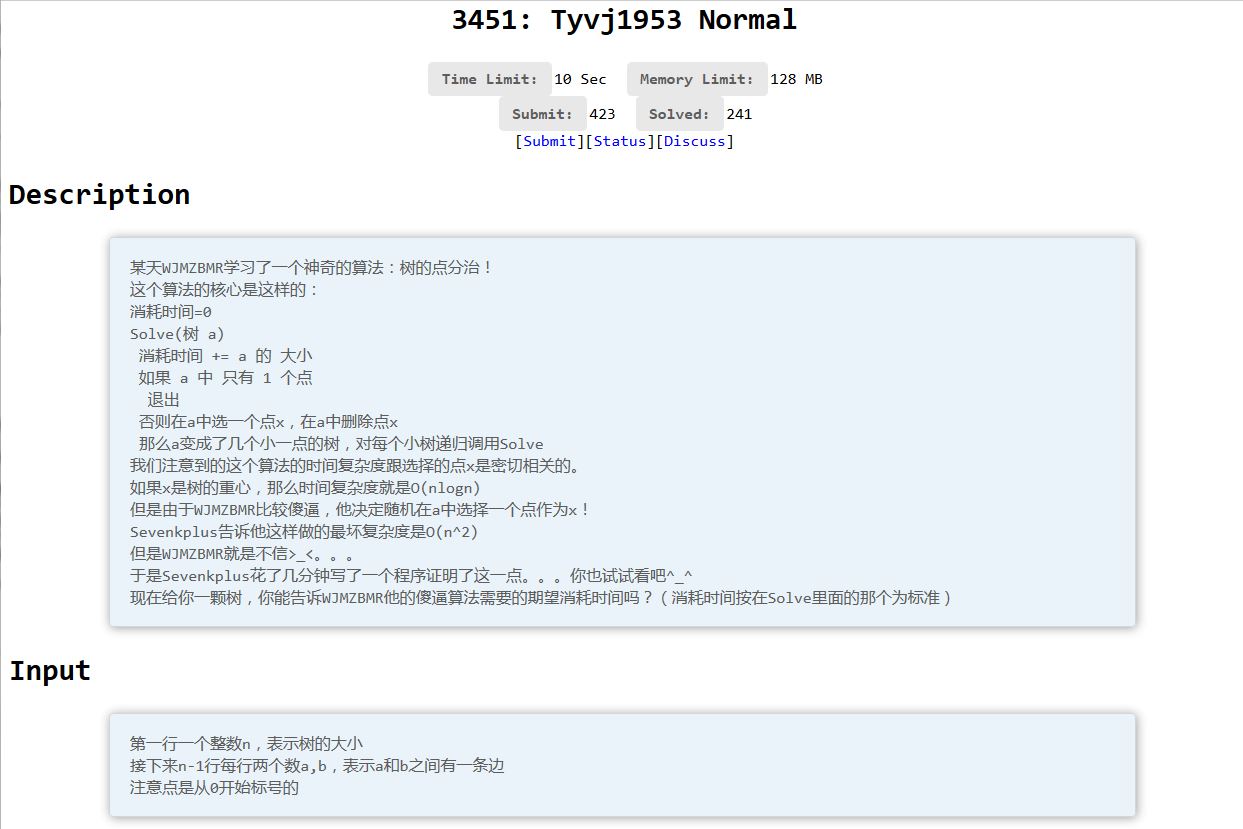

代价理解为重心和每个点这个点对的代价。根据期望的线性性，我们枚举每个点，计算会产生的ij点对的代价即可。
那么，i到j的链上，i必须是第一个被选择的点。
对于i来说，就是1/dis(i,j)。
所以答案就是sigma(i,j) 1/(dis(i,j)+1)。
然而这样计算是n^2的，考虑优化。
如果我们能计算出边长为某个数值的边的数量的话，是不是就能计算答案呢？
统计路径的题，一眼点分治。
考虑怎样计算，我们能dfs出每个子树中距离分治重心为x的点有多少个，然后我们枚举两个点让他们取去组成路径即可。
这显然是个卷积，FFT优化。我们补集转化，先计算全部方案，再减去本身对本身(两个点来自相同子树)的方案。
为什么这样算复杂度正确？因为当当前分治层数一定时，所有子树的最深点的深度总和是O(n)的，并且那个log还会更小。这样分析的话发现复杂度是O(nlog^2n)。
正常的二元关系计算方式是前缀和和当前的卷积贡献，为什么这次不能这样呢？
给你一棵扫把形的树，一半的点形成一条链，显然你会选择扫把的重心(一边是一堆叶子，一边是链)当做重心。
然后你发现链的那边长度为n/2，如果你对每个叶子都和链做一次卷积的话，恭喜你卡成n^2logn，不如暴力......

代码:

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 const int maxn=;
 const int inf=0x3f3f3f3f;
 const double pi = acos(-1.0);
 
 int tim[maxn];
 
 namespace FFT {
     struct Complex {
         double r,i;
         friend Complex operator + (const Complex &a,const Complex &b) { return (Complex){a.r+b.r,a.i+b.i}; }
         friend Complex operator - (const Complex &a,const Complex &b) { return (Complex){a.r-b.r,a.i-b.i}; }
         friend Complex operator * (const Complex &a,const Complex &b) { return (Complex){a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r}; }
     }cp[maxn];
     inline void FFT(Complex* dst,int n,int tpe) {
         for(int i=,j=;i<n;i++) {
             if( i < j ) std::swap(dst[i],dst[j]);
             for(int t=n>>;(j^=t)<t;t>>=) ;
         }
         for(int len=;len<=n;len<<=) {
             const int h = len >> ;
             const Complex per = (Complex){cos(pi*tpe/h),sin(pi*tpe/h)};
             for(int st=;st<n;st+=len) {
                 Complex w = (Complex){1.0,0.0};
                 for(int pos=;pos<h;pos++) {
                     const Complex u = dst[st+pos] , v = dst[st+pos+h] * w;
                     dst[st+pos] = u + v , dst[st+pos+h] = u - v , w = w * per;
                 }
             }
         }
         if( !~tpe ) for(int i=;i<n;i++) dst[i].r /= n;
     }
     inline void mul(int* dst,int n) {
         int len = ;
         while( len <= ( n <<  ) ) len <<= ;
         for(int i=;i<len;i++) cp[i] = (Complex){(double)dst[i],0.0};
         FFT(cp,len,);
         for(int i=;i<len;i++) cp[i] = cp[i] * cp[i];
         FFT(cp,len,-);
         for(int i=;i<len;i++) dst[i] = (int)(cp[i].r+0.5);
     }
 }
 
 namespace Tree {
     int s[maxn],t[maxn<<],nxt[maxn<<];
     int siz[maxn],mxs[maxn],ban[maxn];
     int su[maxn],tp[maxn];
 
     inline void addedge(int from,int to) {
         static int cnt = ;
         t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
     }
     inline void findroot(int pos,int fa,const int &fs,int &rt) {
         siz[pos] =  , mxs[pos] = ;
         for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa && !ban[t[at]] ) findroot(t[at],pos,fs,rt) , siz[pos] += siz[t[at]] , mxs[pos] = std::max( mxs[pos] , siz[t[at]] );
         if( ( mxs[pos] = std::max( mxs[pos] , fs - siz[pos]) ) <= mxs[rt] ) rt = pos;
     }
     inline void dfs(int pos,int fa,int dep,int &mxd) {
         mxd = std::max( mxd , dep ) , ++tp[dep];
         for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa && !ban[t[at]] ) dfs(t[at],pos,dep+,mxd);
     }
     inline void solve(int pos,int fs) {
         int root =  , mxd =  , ths ;
         *mxs = inf, findroot(pos,-,fs,root) , ban[root] = ;
         for(int at=s[root];at;at=nxt[at]) if( !ban[t[at]]) {
             ths =  , dfs(t[at],root,,ths) , mxd = std::max( mxd , ths );
             for(int i=;i<=ths;i++) su[i] += tp[i];
             FFT::mul(tp,ths);
             for(int i=;i<=ths<<;i++) tim[i] -= tp[i];
             memset(tp,,sizeof(int)*(ths<<|));
         }
         ++*su , FFT::mul(su,mxd);
         for(int i=;i<=mxd<<;i++) tim[i] += su[i];
         memset(su,,sizeof(int)*(mxd<<|));
         for(int at=s[root];at;at=nxt[at]) if( !ban[t[at]] ) solve(t[at],siz[t[at]]<siz[root]?siz[t[at]]:fs-siz[root]);
     }
 }
 
 int main() {
     static int n;
     static long double ans;
     scanf("%d",&n);
     for(int i=,a,b;i<n;i++) scanf("%d%d",&a,&b) , ++a , ++b , Tree::addedge(a,b) , Tree::addedge(b,a);
     Tree::solve(,n) , ans = n;
     for(int i=;i<=n<<;i++) ans += (long double) tim[i] / ( i +  );
     printf("%0.4Lf\n",ans);
     return ;
 }

ここでこのまま
即使在这里就这样
僕が消えてしまっても 誰も知らずに
我消失不见了 谁也不会知道吧
明日が来るのだろう
明天依然会来临吧
わずか 世界のひとかけらに過ぎない
我仅仅是 这个世界的微小碎屑
ひとりを夜が包む
夜晚怀抱孤独的身影