tyvj1728 普通平衡树

为了彻底理解树状数组，试着用树状数组做了下普通平衡树

而树状数组只能离线做，或者保证值的大小在数组可承受的范围内也是可以的，因为要求离线是因为必须事前对所有数离散化。

然后我们看刘汝佳蓝书上的图

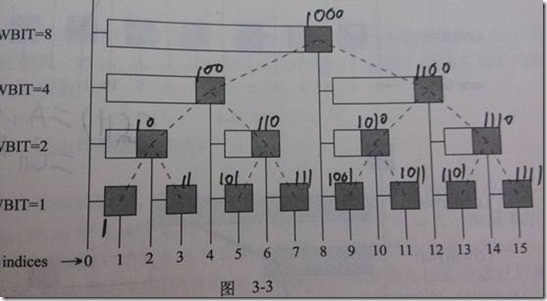
利用如下代码，可以找到所有前缀和中第一个大于等于k的

 int kth(int k) {
     int ans=;
     for(int i=;i>=; --i) {
         ans += <<i;
         if(ans>=sz || C[ans]>=k) ans-=<<i;
         else k-=C[ans];
     }
     return seq[ans+];
 }        

什么原理呢，我们这么理解，把树状数组看成一棵树，事实上他的节点编号的中序遍历是有序的，跟平衡树有异曲同工之妙，假设现在在(1000)2这个点，如果往左走，就相当于没有取[1,8]，接着在[1,7]中取，如果往右走，就相当于取了[1,8]，接着在[9,15]中取，至于应该往左走还是往右走跟平衡树找第k大是一样的。然后可以发现，平衡树相当于是在[1,n]上建树的，而二叉索引树是在[1,2^k](k为2^k>=n的最小正整数)。

给出普通平衡树的完整代码

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>

 using namespace std;

 const int Maxn=;

 int C[Maxn],sz;

 int sum(int x) {
     int ret=;
     for(;<x && x<=sz; x-=x&-x) ret+=C[x];
     return ret;
 }

 void add(int x,int d) {
     for(;<x&&x<=sz; x+= x&-x) C[x]+=d;
 }

 int seq[Maxn],tot;
 void HashInit() {
     sort(seq+,seq+tot+);
     sz = unique (seq+,seq+tot+) - (seq+);
 }
 int hash(int x) {
     return lower_bound(seq+,seq+sz+,x) - seq;
 }

 int opt[Maxn],num[Maxn];

 int kth(int k) {
     int ans=;
     for(int i=;i>=; --i) {
         ans += <<i;
         if(ans>=sz || C[ans]>=k) ans-=<<i;
         else k-=C[ans];
     }
     return seq[ans+];
 }            

 int main() {
 #ifdef DEBUG
     freopen("in.txt","r",stdin);
 //    freopen("out.txt","w",stdout);
 #endif

     int n;
     scanf("%d",&n);
     for(int i=;i<=n;i++) {
         scanf("%d%d",opt+i,num+i);
         if(opt[i]!=) seq[++tot] = num[i];
     }

     HashInit();

     for(int i=;i<=n;i++) {
         if(opt[i]==) add(hash(num[i]),);
         if(opt[i]==) add(hash(num[i]),-);
         if(opt[i]==) printf("%d\n",sum(hash(num[i])-)+);
         if(opt[i]==) printf("%d\n",kth(num[i]));
         if(opt[i]==) printf("%d\n",kth(sum(hash(num[i])-)));
         if(opt[i]==) printf("%d\n",kth(sum(hash(num[i]))+));
     }    

     return ;
 }