[洛谷P2704] [NOI2001]炮兵阵地

洛谷题目链接:[NOI2001]炮兵阵地

题目描述

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

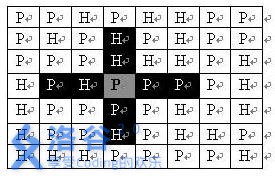
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入输出格式

输入格式：

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

输出格式：

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

输入输出样例

输入样例#1：

5 4

PHPP

PPHH

PPPP

PHPP

PHHP

输出样例#1：

6

一句话题意: 在一个\(n*m\)的矩阵中有一些地方可以放置炮兵,一个炮兵的攻击范围是上下左右四个方向拓展两个格子.并且在炮兵可以攻击到的地方不能再放置炮兵.在山地同样不能放置炮兵.问最多能放置多少炮兵.

题解: 因为\(m\)的范围很小,可以考虑状态压缩.我们用\(f[i][B][C]\)表示到到第\(i\)行,上一行的状态为\(j\),这一行的状态为\(k\)的方案数.假设用\(A\)表示上上行的状态,那么对于合法的状态,则有:\(f[i][B][C]=max(f[i][B][C], f[i-1][A][B])\).

但是这样做的话空间复杂度是\(O(1000*2^ {10} * 2 ^{10})\)的,显然这是存不下的.所以我们可以考虑使用滚动数组,将行所在的那一维滚动处理,只存3行(这一行,上一行,上上行),这样空间复杂度就变成了\(O(3*2^ {10} * 2 ^{10})\),就可以存下了.

然后因为第1,2行没有上上行,所以可以将这两行单独拿出来处理.

然而这样做在时间上有点慢,时间复杂度是\(O(100*2 ^ {10} * 2 ^{10})\)(虽然这道题可以卡着1s过),如果要优化的话可以考虑将所有可行状态用数组存下来,每次只遍历可行状态可以减小时间复杂度.

#include<bits/stdc++.h>
using namespace std;
const int N=100+5;
const int M=10+5;

int n, m, a[N], cnt[(1<<11)], ans = 0;
int f[3][(1<<11)][(1<<11)];
//line, last status and this status

int calc(int con){
    int res = 0;
    for(int i=0;i<=11;i++)
		if((con>>i) & 1) res++;
    return res;
}

int main(){
    //freopen("cannon.in", "r", stdin);
	//freopen("cannon.out", "w", stdout);
    char ch; cin >> n >> m;
    for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
		    cin >> ch, a[i] += ((ch=='H')<<j);
    int U=(1<<m)-1;
    for(int i=0;i<=U;i++) cnt[i] = calc(i);

    for(int i=0;i<=U;i++){
		if((i&a[0]) || ((i<<1)&i) || ((i<<2)&i)) continue;
		f[0][0][i] = cnt[i];
		for(int j=0;j<=U;j++){
		    if((j&a[1]) || ((j<<1)&j) || ((j<<2)&j) || (i&j)) continue;
		    f[1][i][j] = cnt[j]+cnt[i];
		}
    }

    for(int i=2;i<n;i++)
		for(int A=0;A<=U;A++){
		    if((A&a[i-2]) || ((A<<1)&A) || ((A<<2)&A)) continue;
			for(int B=0;B<=U;B++){
				if((B&a[i-1]) || ((B<<1)&B) || ((B<<2)&B) || (B&A)) continue;
				for(int C=0;C<=U;C++){
				    if((C&a[i]) || ((C<<1)&C) || ((C<<2)&C) || (C&A) || (C&B)) continue;
				    f[i%3][B][C] = max(f[(i-1)%3][A][B]+cnt[C], f[i%3][B][C]);
				}
		    }
		}
    for(int i=0;i<=U;i++)
		for(int j=0;j<=U;j++)
		    ans = max(ans, f[(n-1)%3][i][j]);
    cout << ans << endl;
    return 0;
}