POJ 2826 An Easy Problem?!（线段交点+简单计算）

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width. 

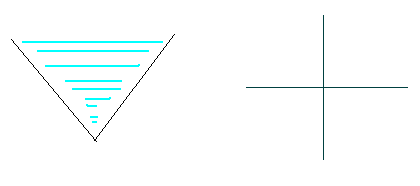
Your mission is to calculate how much rain these two boards can collect. 

Input

The first line contains the number of test cases. 
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one. 

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected. 

 

题目大意：给两条线段，问这两条线段可以接多少面积的雨水。

思路：没有相交的线段不能接水。因为雨是垂直下落的，有时可能会有一条线段遮住了接水的地方导致无法接水。

PS：输出就不加EPS可能会WA，比如某个计算结果是0.004999999999……

 

代码（32MS）：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <cmath>
 using namespace std;

 const double EPS = 1e-;
 const double PI = acos(-1.0);//3.14159265358979323846

 inline int sgn(double x) {
     return (x > EPS) - (x < -EPS);
 }

 struct Point {
     double x, y;
     Point() {}
     Point(double x, double y): x(x), y(y) {}
     void read() {
         scanf("%lf%lf", &x, &y);
     }
     bool operator < (const Point &rhs) const {
         if(y != rhs.y) return y < rhs.y;
         return x < rhs.x;
     }
     Point operator + (const Point &rhs) const {
         return Point(x + rhs.x, y + rhs.y);
     }
     Point operator - (const Point &rhs) const {
         return Point(x - rhs.x, y - rhs.y);
     }
     Point operator * (const int &b) const {
         return Point(x * b, y * b);
     }
     Point operator / (const int &b) const {
         return Point(x / b, y / b);
     }
     double length() const {
         return sqrt(x * x + y * y);
     }
     Point unit() const {
         return *this / length();
     }
 };
 typedef Point Vector;

 double dist(const Point &a, const Point &b) {
     return (a - b).length();
 }

 double cross(const Point &a, const Point &b) {
     return a.x * b.y - a.y * b.x;
 }
 //ret >= 0 means turn left
 double cross(const Point &sp, const Point &ed, const Point &op) {
     return sgn(cross(sp - op, ed - op));
 }

 double area(const Point& a, const Point &b, const Point &c) {
     return fabs(cross(a - c, b - c)) / ;
 }

 struct Seg {
     Point st, ed;
     Seg() {}
     Seg(Point st, Point ed): st(st), ed(ed) {}
     void read() {
         st.read(); ed.read();
     }
 };
 typedef Seg Line;

 bool isIntersected(const Point &s1, const Point &e1, const Point &s2, const Point &e2) {
     return (max(s1.x, e1.x) >= min(s2.x, e2.x)) &&
         (max(s2.x, e2.x) >= min(s1.x, e1.x)) &&
         (max(s1.y, e1.y) >= min(s2.y, e2.y)) &&
         (max(s2.y, e2.y) >= min(s1.y, e1.y)) &&
         (cross(s2, e1, s1) * cross(e1, e2, s1) >= ) &&
         (cross(s1, e2, s2) * cross(e2, e1, s2) >= );
 }

 bool isIntersected(const Seg &a, const Seg &b) {
     return isIntersected(a.st, a.ed, b.st, b.ed);
 }

 bool isParallel(const Seg &a, const Seg &b) {
     return sgn(cross(a.ed - a.st, b.ed - b.st)) == ;
 }

 //return Ax + By + C =0 's A, B, C
 void Coefficient(const Line &L, double &A, double &B, double &C) {
     A = L.ed.y - L.st.y;
     B = L.st.x - L.ed.x;
     C = L.ed.x * L.st.y - L.st.x * L.ed.y;
 }

 Point intersection(const Line &a, const Line &b) {
     double A1, B1, C1;
     double A2, B2, C2;
     Coefficient(a, A1, B1, C1);
     Coefficient(b, A2, B2, C2);
     Point I;
     I.x = - (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
     I.y =   (A2 * C1 - A1 * C2) / (A1 * B2 - A2 * B1);
     return I;
 }

 bool isEqual(const Line &a, const Line &b) {
     double A1, B1, C1;
     double A2, B2, C2;
     Coefficient(a, A1, B1, C1);
     Coefficient(b, A2, B2, C2);
     return sgn(A1 * B2 - A2 * B1) ==  && sgn(A1 * C2 - A2 * C1) ==  && sgn(B1 * C2 - B2 * C1) == ;
 }

 /*******************************************************************************************/

 Seg a, b;
 int n;

 double solve() {
     if(!isIntersected(a, b)) return ;
     Seg tmp(Point(, ), Point(, ));
     if(isParallel(a, tmp) || isParallel(b, tmp) || isParallel(a, b)) return ;
     if(a.st.y > a.ed.y) swap(a.st, a.ed);
     if(b.st.y > b.ed.y) swap(b.st, b.ed);
     Point O = intersection(a, b);
     if(b.ed < a.ed) swap(a, b);
     if(sgn(a.ed.x - O.x) == sgn(b.ed.x - O.x) && (sgn(b.ed.x - O.x) * sgn(cross(b.ed, O, a.ed)) >= ) &&
        sgn(fabs(b.ed.x - O.x) - fabs(a.ed.x - O.x)) >= ) return ;
     Point A = a.ed;
     tmp = Seg(A, Point(A.x + , A.y));
     Point B = intersection(tmp, b);
     return area(A, B, O);
 }

 int main() {
     scanf("%d", &n);
     for(int i = ; i < n; ++i) {
         a.read(), b.read();
         printf("%.2f\n", solve() + EPS);
     }
 }