Visual Studio2017中如何让ADO.NET实体数据模型[EntityFramework]支持MariaDB&MySQL数据源

近期由于工作需要，需要重新修改设计系统的ADO.NET实体数据模型.edmx文件中间，在完成实际中途遇到一些实际使用问题，特此记录。

1. Visual Studio 2017 无法以实体设计模式打开MySQL&MaraiDB 相关.edmx 文件，出现如下错误：

　　

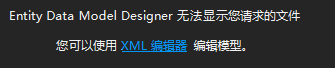
  如何解决： 

     1.确保已安装 Entity Framework 6工具

       如已安装，则直接跳过1步骤，如未安装，则通过 工具-->获取工具和功能(修改Visual Studio)-->单个组件，勾选Entity Framework 6 工具，安装即可。

     2. 安装相应版本 Connector/Net 和 MySQL for Visual Studio 即可

 　 

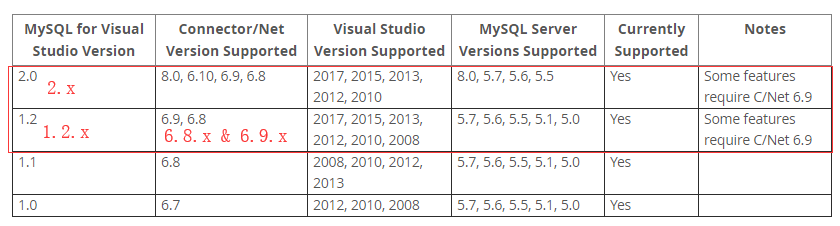
找到Visual Studio 2017 对应支持版本即可，这里我选择的 mysql-for-visualstudio-1.2.7.msi & Connector/Net 6.9.11 安装完毕之后重启VisualStudio之后即可以设计模式打开MariaDB&MySQL对应的.edmx 文件

  PS:

　　1. 安装是注意对照表中的版本进行安装

　　2. 如果找不到对应版本，可以尝试点击查看历史版本，然后下载对应版本进行安装

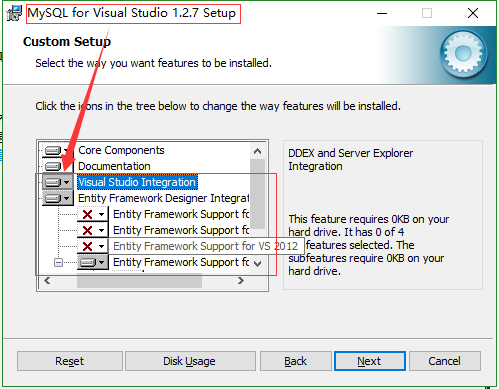
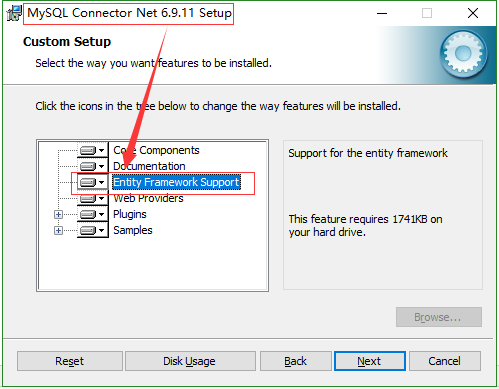
3.安装时注意选择勾选：

Connector/Net: 勾选 Enity Framework Support

mysql-for-visualstudio 勾选: Visual Studio Integration 和 指定Visual Studio版本的 Entity Framework Designer Intgration

如图示：

　　

如不清楚如何处理，请选择完整安装即可。

2. Visual Studio 2017 但是无法进行根据MySQL or MariaDB 数据库进行更新实体模型等操作

   错误如下：找不到与之兼容的实体框架数据库提供程序

 

　

 

 如何解决:

  使用Nuget添加对应的Entity Framework, MySql.Web,MySql.Data,MySql.Data.Entity包即可。

  我这里添加的版本为：Entity Framework 6.1.3,MySql.Web 6.9.11,MySql.Data 6.9.11,MySql.Data.Entity 6.9.11 

  添加完毕后，重新生成项目即可进行:从数据库更新实体等操作，如图：以可进行实体更新等操作

 

  

PS:

   1. 这里的这里的Nuget包版本一定要与之对应，否则也可能会造成无法识别提供程序等错误

   2. 安装Nuget包时，最好手动将原来的错误的依赖删除后，重新使用Nuget进行添加，并重新生成项目。

 

这里在使用EntityFramework 6.1.0 及以上包 + MySql.6.9.9 系列包时，将出现无法识别提供程序等错误，使用MySql 6.9.11 系列包时正常使用，无错误发生。