[BZOJ5305][Haoi2018]苹果树 组合数

题目描述

小 C 在自己家的花园里种了一棵苹果树, 树上每个结点都有恰好两个分支. 经过细心的观察, 小 C 发现每一天这棵树都会生长出一个新的结点.

第一天的时候, 果树会长出一个根结点, 以后每一天, 果树会随机选择一个当前树中没有长出过结点 的分支, 然后在这个分支上长出一个新结点, 新结点与分支所属的结点之间连接上一条边.

小 C 定义一棵果树的不便度为树上两两结点之间的距离之和, 两个结点之间 的距离定义为从一个点走到另一个点的路径经过的边数.

现在他非常好奇, 如果 NNN 天之后小 G 来他家摘苹果, 这个不便度的期望 EEE 是多少. 但是小 C 讨厌分数, 所以他只想知道E×N!E \times N !E×N! 对 PPP 取模的结果, 可以证明这是一个整数.

输入输出格式

输入格式：

从标准输入中读入数据. 一行两个整数 NNN (N<=2000), PPP .

输出格式：

输出到标准输出中. 输出一个整数表示答案．

输入输出样例

输入样例#1： 复制

3 610745795

输出样例#1： 复制

24

输入样例#2： 复制

305 1000000007

输出样例#2： 复制

865018107

说明

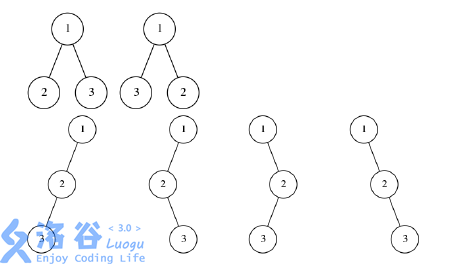
以上是所有 N=3N = 3N=3 时可能的苹果树形态, 其中编号表示这个结点是第几天生 长出来的, 显然每种情况两两结点的距离均为 444 .

考虑n个节点二叉树方案为n!

考虑边的贡献。

设子树大小为sz,则在不考虑编号的情况下经过此边sz*(n-sz)次

方案数为子树内方案*子树外方案。

由于i节点子树内节点编号>i，所以方案为sz!*C(n-i,sz-1)。

子树外方案为i!*(i+1-2)*(i+2-2)*(i+3-2)*......*(n-sz+1-2)。

化简为

i*(i-1)*(n-sz-1)!

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #define ll long long
 using namespace std;
 inline ll read() {
     ll x=,f=;char ch=getchar();
     for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
     for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
     return x*f;
 }
 ll n,p;
 ll jc[],c[][];
 int main() {
     n=read(),p=read();
     c[][]=;
     jc[]=;
     for(int i=;i<=n;i++) {
         c[i][]=;
         jc[i]=jc[i-]*i;jc[i]%=p;
         for(int j=;j<=i;j++) c[i][j]=(c[i-][j]+c[i-][j-])%p;
     }
     ll ans=;
     for(int i=;i<=n;i++) {
         for(int sz=;sz<=n-i+;sz++) {
             ans+=sz*(n-sz)*i*(i-)%p*c[n-i][sz-]%p*jc[sz]%p*jc[n-sz-]%p;
             ans%=p;
         }
     }
     printf("%lld\n",ans);
 }