HDU.2640 Queuing (矩阵快速幂)

HDU.2640 Queuing (矩阵快速幂)

题意分析

不妨令f为1，m为0，那么题目的意思为，求长度为n的01序列，求其中不含111或者101这样串的个数对M取模的值。

用F(n)表示串长为n的合法串的个数。

首先不难通过枚举发现F(0) = 0, F(1) =2, F(3) = 6, F(4) = 9, F(5) = 15.然后引用网上如何求解递推公式的详细解释：

用f(n)表示n个人满足条件的结果，那么如果最后一个人是m的话，那么前n-1个满足条件即可，就是f(n-1)；

如果最后一个是f那么这个还无法推出结果，那么往前再考虑一位：那么后三位可能是：mmf, fmf, mff, fff，其中fff和fmf不满足题意所以我们不考虑，但是如果是

mmf的话那么前n-3可以找满足条件的即：f(n-3)；如果是mff的话，再往前考虑一位的话只有mmff满足条件即：f(n-4)

所以f(n)=f(n-1)+f(n-3)+f(n-4)

我个人比较喜欢用Trie示意图的方法来求解递推结果，如图所示：

然后构造如图矩阵

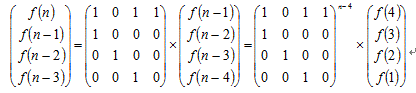
代码总览

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#define INF 0x3f3f3f3f
#define nmax 200
#define MEM(x) memset(x,0,sizeof(x))
using namespace std;
const int Dmax = 11;
int N = 4;
int MOD;
int st[] = {0,2,4,6,9,15};
typedef struct{
    int matrix[Dmax][Dmax];
    void init()//初始化为单位矩阵
    {
        memset(matrix,0,sizeof(matrix));
        for(int i = 0; i<Dmax;++i) matrix[i][i] = 1;
    }
}MAT;
MAT ADD(MAT a, MAT b)
{
    for(int i = 0; i<N;++i){
        for(int j = 0;j<N;++j){
            a.matrix[i][j] +=b.matrix[i][j];
            a.matrix[i][j] %= MOD;
        }
    }
    return a;
}
MAT MUL(MAT a, MAT b)
{
    MAT ans;
    for(int i = 0; i<N;++i){
        for(int j = 0; j<N;++j){
            ans.matrix[i][j] = 0;
            for(int k = 0; k<N;++k){
                ans.matrix[i][j] += ( (a.matrix[i][k] % MOD) * (b.matrix[k][j] % MOD) ) % MOD;
            }
            ans.matrix[i][j] %= MOD;
        }
    }
    return ans;
}
MAT POW(MAT a, int t)
{
    MAT ans; ans.init();
    while(t){
        if(t&1) ans = MUL(ans,a);
        t>>=1;
        a = MUL(a,a);
    }
    return ans;
}
void OUT(MAT a)
{
    for(int i = 0; i<N;++i){
        for(int j =  0; j<N;++j){
            printf("%5d",a.matrix[i][j]);
        }
        printf("\n");
    }
}
void IN(MAT & a,MAT & temp)
{
    memset(a.matrix,0,sizeof(a.matrix));
    memset(temp.matrix,0,sizeof(temp.matrix));
    for(int i = 0; i<N;++i) a.matrix[i][0] = st[5-i];
    for(int i = 0; i<N;++i){if(i == 1) continue;temp.matrix[0][i] = 1;}
    for(int i = 1;i<N;++i) temp.matrix[i][i-1] = 1;
}
void CAL(MAT a)
{
    printf("%d\n",a.matrix[0][0] % MOD);
}
int main()
{
    //freopen("in.txt","r",stdin);
    int K;
    while(scanf("%d%d",&K,&MOD) != EOF){
        if(K<=5){
            printf("%d\n",st[K]%MOD);
            continue;
        }
        MAT init,temp;
        IN(init,temp);
        temp = POW(temp,K-5);
        temp = MUL(temp,init);
        CAL(temp);
    }
    return 0;
}