bzoj 1568 [JSOI2008]Blue Mary开公司 超哥线段树

[JSOI2008]Blue Mary开公司

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 1808  Solved: 639
[Submit][Status][Discuss]

Description

Input

第一行 ：一个整数N ，表示方案和询问的总数。 

接下来N行，每行开头一个单词“Query”或“Project”。 

若单词为Query，则后接一个整数T，表示Blue Mary询问第T天的最大收益。 

若单词为Project，则后接两个实数S，P，表示该种设计方案第一天的收益S，以及以后每天比上一天多出的收益P。

1 <= N <= 100000 1 <= T <=50000 0 < P < 100，| S | <= 10^6 

提示：本题读写数据量可能相当巨大，请选手注意选择高效的文件读写方式。

Output

对于每一个Query，输出一个整数，表示询问的答案，并精确到整百元（以百元为单位，

例如：该天最大收益为210或290时，均应该输出2）。没有方案时回答询问要输出0

Sample Input

10
Project 5.10200 0.65000
Project 2.76200 1.43000
Query 4
Query 2
Project 3.80200 1.17000
Query 2
Query 3
Query 1
Project 4.58200 0.91000
Project 5.36200 0.39000

Sample Output

0
0
0
0
0

HINT

 

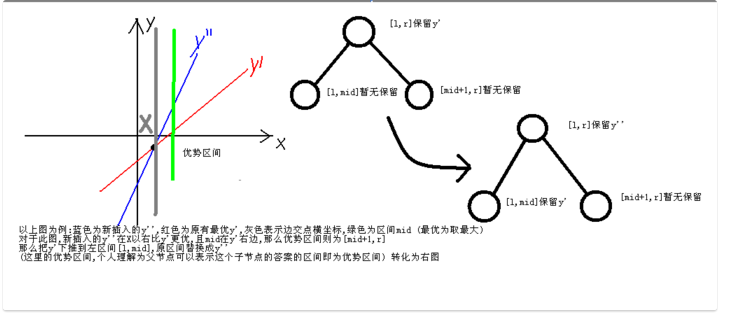
题解：可以看出许多条一次函数，然后每次询问的时候就是求一个x的坐标的答

　　　案，超哥线段树可以说就是永久标记维护各段的最大值。

　　　　

 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<iostream>
 #include<cmath>
 #include<queue>
 #include<map>

 #define N 50007
 #define ls p<<1
 #define rs p<<1|1
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')f=-;ch=getchar();}
     while(isdigit(ch)){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int n,tot;
 double ans;
 int tr[N<<];
 char ch[];
 struct Node
 {
     double k,b;
 }a[N<<];

 bool judge(int x,int y,int t)
 {
     t--;
     return a[x].b+a[x].k*t>a[y].b+a[y].k*t;
 }
 void ins(int p,int l,int r,int x)
 {
     if (l==r)
     {
         if (judge(x,tr[p],l)) tr[p]=x;
         return;
     }
     int mid=(l+r)>>;
     if (a[x].k>a[tr[p]].k)
     {
         if (judge(x,tr[p],mid)) ins(ls,l,mid,tr[p]),tr[p]=x;
         else ins(rs,mid+,r,x);
     }
     else
     {
         if (judge(x,tr[p],mid)) ins(rs,mid+,r,tr[p]),tr[p]=x;
         else ins(ls,l,mid,x);
     }
 }
 void query(int p,int l,int r,int x)
 {
     ans=max(ans,a[tr[p]].k*(x-)+a[tr[p]].b);
     if (l==r) return;
     int mid=(l+r)>>;
     if (x<=mid) query(ls,l,mid,x);
     else query(rs,mid+,r,x);
 }
 int main()
 {
     n=read();
     for (int i=;i<=n;i++)
     {
         scanf("%s",ch);
         if (ch[]=='P')
         {
             tot++;
             scanf("%lf%lf",&a[tot].b,&a[tot].k);
             ins(,,n,tot);
         }
         else
         {
             ans=;query(,,n,read());
             printf("%d\n",(int)ans/);
         }
     }
 }