再论EM算法的收敛性和K-Means的收敛性

标签（空格分隔）：机器学习

（最近被一波波的笔试+面试淹没了，但是在有两次面试时被问到了同一个问题：K-Means算法的收敛性。在网上查阅了很多资料，并没有看到很清晰的解释，所以希望可以从K-Means与EM算法的关系，以及EM算法本身的收敛性证明中找到蛛丝马迹，下次不要再掉坑啊。。）

EM算法的收敛性

1.通过极大似然估计建立目标函数：

$l(\theta) = \sum_{i=1}^{m}log\ p(x;\theta) = \sum_{i=1}^{m}log\sum_{z}p(x,z;\theta)$

通过EM算法来找到似然函数的极大值，思路如下：
希望找到最好的参数$\theta$，能够使最大似然目标函数取最大值。但是直接计算 $l(\theta) = \sum_{i=1}^{m}log\sum_{z}p(x,z;\theta)$比较困难，所以我们希望能够找到一个不带隐变量$z$的函数$\gamma(x|\theta) \leq l(x,z;\theta)$恒成立，并用$\gamma(x|\theta)$逼近目标函数。
如下图所示：

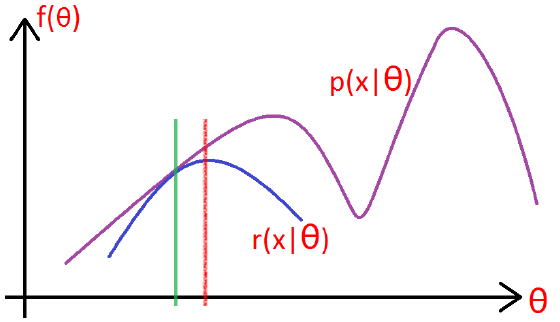
在绿色线位置，找到一个$\gamma$函数，能够使得该函数最接近目标函数，
固定$\gamma$函数，找到最大值，然后更新$\theta$,得到红线；
对于红线位置的参数$\theta$：
固定$\theta$，找到一个最好的函数$\gamma$，使得该函数更接近目标函数。
重复该过程，直到收敛到局部最大值。

2. 从Jensen不等式的角度来推导

令$Q_{i}$是$z$的一个分布，$Q_{i} \geq 0$，则：

$l(\theta) = \sum_{i=1}^{m}log\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) $
$ = \sum_{i=1}^{m}log\sum_{z^{(i)}}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$
$\geq \sum_{i=1}^{m}\sum_{z^{(i)}}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$

(对于log函数的Jensen不等式)

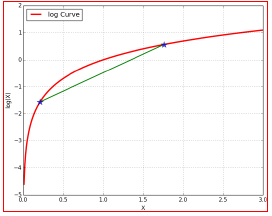
3.使等号成立的Q

尽量使$\geq$取等号，相当于找到一个最逼近的下界：也就是Jensen不等式中，$\frac{f(x_{1})+f(x_{2})}{2} \geq f(\frac{x_{1}+x_{2}}{2})$，当且仅当$x_{1} = x_{2}$时等号成立(很关键)。

对于EM的目标来说：应该使得$log$函数的自变量恒为常数，即：
$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} = C$
也就是分子的联合概率与分母的z的分布应该成正比，而由于$Q$是z的一个分布，所以应该保证$\sum_{z}Q_{i}(z^{(i)}) = 1$
故$Q = \frac{p}{p对z的归一化因子}$

$Q_{i}(z^{(i)}) = \frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z}p(x^{(i)},z^{(i)};\theta)}$
$= \frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} = p(z^{(i)}|x^{(i)};\theta)$

4.EM算法的框架

由上面的推导，可以得出EM的框架：

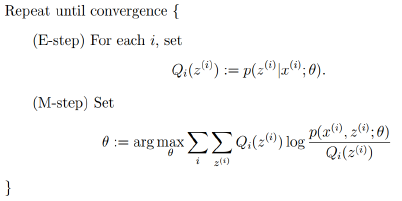
回到最初的思路，寻找一个最好的$\gamma$函数来逼近目标函数，然后找$\gamma$函数的最大值来更新参数$\theta$:

E-step: 根据当前的参数$\theta$找到一个最优的函数$\gamma$能够在当前位置最好的逼近目标函数；
M-step: 对于当前找到的$\gamma$函数，求函数取最大值时的参数$\theta$的值。

K-Means的收敛性

通过上面的分析，我们可以知道，在EM框架下，求得的参数$\theta$一定是收敛的，能够找到似然函数的最大值。那么K-Means是如何来保证收敛的呢？

目标函数

假设使用平方误差作为目标函数：
$J(\mu_{1},\mu_{2},...,\mu_{k}) = \frac{1}{2}\sum_{j=1}^{K}\sum_{i=1}^{N}(x_{i}-\mu_{j})^{2}$

E-Step

固定参数$\mu_{k}$, 将每个数据点分配到距离它本身最近的一个簇类中：
\[
\gamma_{nk} =
\begin{cases}
1, & \text{if $k = argmin_{j}||x_{n}-\mu_{j}||^{2}$ } \\
0, & \text{otherwise}
\end{cases}
\]

M-Step

固定数据点的分配，更新参数（中心点）$\mu_{k}$:
$\mu_{k} = \frac{\sum_{n}\gamma_{nk}x_{n}}{\sum_{n}\gamma_{nk}}$

所以，答案有了吧。为啥K-means会收敛呢？目标是使损失函数最小，在E-step时，找到一个最逼近目标的函数$\gamma$；在M-step时，固定函数$\gamma$，更新均值$\mu$（找到当前函数下的最好的值）。所以一定会收敛了~