前N个自然数的随机置换

来自：【数据结构与算法分析——C语言描述】练习2.7

问题描述：假设需要生成前N个自然数的一个随机置换。例如，{4,1,2,5,2} 和 {3,1,4,2,5} 就是合法的置换，但 {5,4,1,2,1} 却不是，因为数1出现了两次而数 3 缺没有。这个程序常常用于模拟一些算法。我们假设存在一个随机数生成器 randInt(i, j) ，它以相同的概率生成 i 和 j 之间的一个整数。

下面是三个算法：

1.如下填入 A[0] 到 A[N-1] 的数组 A；为了填入 A[i] ，生成随机数直到它不同于已经生成的 A[0], A[1],  ... ,  A[i-1] 时，再将其填入 A[i] 。

2.同算法1，但是要保存一个附加的数组，称之为 Used（用过的）数组。当一个随机数 Ran 最初被放入数组A的时候，置Used[Ran]=1。这就是说，当用一个随机数填入 A[i] 时，可以用一步来测试是否该随机数已经被使用，而不是像第一个算法那样（可能）进行 i 步测试。

3.填写该数组使得 A[i] = i + 1。然后

for(i = 1; i < N; i++)
    swap(&A[i], &A[randInt(0, i)]);

题目中有说“我们假设存在一个随机数RandInt(i, j)”，既然如此，暂时不必考虑其内部实现以及内存限制，只根据这个接口考虑算法即可。

算法1

i = 0;
while (i < N)
{
    ran = randInt(0, N);
    for (k = 0; k < i; k++)
    {
        if (A[k] == ran)
            break;
    }
    if (k == i)
    {
        A[i] = ran;
        count++;
    }
}

以循环次数作为时间度量。循环从i=0到i=n-1写出n个不重复随机数，因为生成第i个不重复随机数的概率是(N-i)/N，所以理论上经过N/(N-i)次生成，得到不重复随机数的概率为1。所以总耗时为

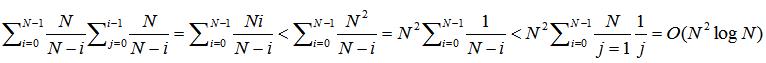
这里做了分子的放大，以及这个调和和公式：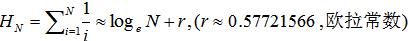

该算法的时间复杂度即为O(N²logN)。

算法2

i = 0;
while (i < N)
{
    ran = randInt(0, N);
    if (used[ran] == 0)
    {
        A[i] = ran;
        used[ran] = 1;
        i++;
    }
}

算法 2 比算法 1 少了内层的 for 循环，所以时间复杂度降了一阶，即为 O(NlogN)。

算法3

for (i = 0; i < N; i++)
    A[i] = i + 1;
for (i = 0; i < N; i++)
    swap(&A[i], &A[randInt(0, i)]);

时间复杂度显然是线性级的，O(N)。