Machine learning(3-Linear Algebra Review )
1、Matrices and vectors
- Matrix :Rectangular array of numbers
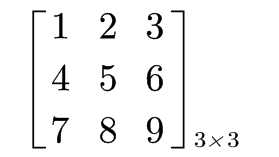
a notation R3×3
- Vector : An n×1 matrix
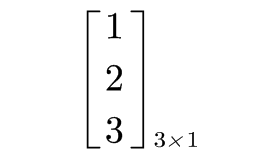
this is a three dimensional vector , a notation R3
2、Addition and scalar multiplication
3、Matrix-vector multiplication
内标相同即可乘,前行×后列得一行 (可运用Python直接计算,参考用python检查矩阵的计算)



4、Matrix-matrix multiplication
- Same as above
5、Matrix multiplication properties
- No commutative A×B ≠ B×A (B is not identity matrix)
- Yes associative (A×B)×C=A×(B×C)

- For any matrix A, A×I = I×A = A
6、Inverse and transpose
- Inverse :
we can use python to implement and for example :
from numpy import *
# 自行判断|A|≠0
# 求逆矩阵 ,建议:取小数点后一位化为分数
A = mat([[1, -1, 1],
[1, 1, 0],
[-1, 0, 1]])
B = A.I
print(B)
# [ 0.33333333 0.33333333 -0.33333333]
# [-0.33333333 0.66666667 0.33333333]
# [ 0.33333333 0.33333333 0.66666667]
# 0.333≈ 1/3 ,0.667≈ 2/3
- Transpose :
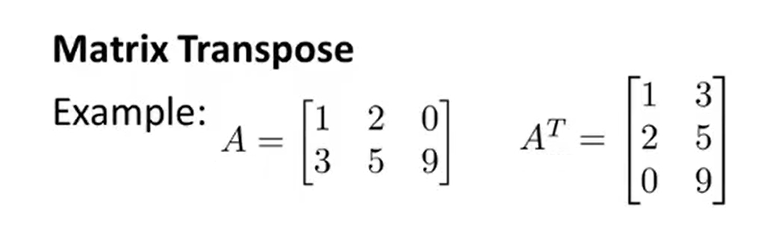
Machine learning(3-Linear Algebra Review )的更多相关文章
- 机器学习---最小二乘线性回归模型的5个基本假设(Machine Learning Least Squares Linear Regression Assumptions)
在之前的文章<机器学习---线性回归(Machine Learning Linear Regression)>中说到,使用最小二乘回归模型需要满足一些假设条件.但是这些假设条件却往往是人们 ...
- Codeforces 940F Machine Learning (带修改莫队)
题目链接 Codeforces Round #466 (Div. 2) Problem F 题意 给定一列数和若干个询问,每一次询问要求集合$\left\{c_{0}, c_{1}, c_{2}, ...
- CF940F Machine Learning(带修莫队)
首先显然应该把数组离散化,然后发现是个带修莫队裸题,但是求mex比较讨厌,怎么办?其实可以这样求:记录每个数出现的次数,以及出现次数的出现次数.至于求mex,直接暴力扫最小的出现次数的出现次数为0的正 ...
- Fast and accurate bacterial species identification in urine specimens using LC-MS/MS mass spectrometry and machine learning (解读人:闫克强)
文献名:Fast and accurate bacterial species identification in urine specimens using LC-MS/MS mass spectr ...
- 机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
在<机器学习---线性回归(Machine Learning Linear Regression)>一文中,我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法.现在,让我们来实践 ...
- 算法库:基础线性代数子程序库(Basic Linear Algebra Subprograms,BLAS)介绍
调试DeepFlow光流算法,由于作者给出的算法是基于Linux系统的,所以要在Windows上运行,不得不做大量的修改工作.移植到Windows平台,除了一些头文件找不到外,还有一些函数也找不到.这 ...
- Pattern Recognition and Machine Learning (preface translation)
前言 鉴于机器学习产生自计算机科学,模式识别却起源于工程学.然而,这些活动能被看做同一个领域的两个方面,并且他们同时在这过去的十年间经历了本质上的发展.特别是,当图像模型已经作为一个用来描述和应用概率 ...
- Targeted Learning R Packages for Causal Inference and Machine Learning(转)
Targeted learning methods build machine-learning-based estimators of parameters defined as features ...
- Machine learning(1-Introduction)
1.What is machine learning Field of study that gives computers the ability to learn without being ex ...
- A brief introduction to weakly supervised learning(简要介绍弱监督学习)
by 南大周志华 摘要 监督学习技术通过学习大量训练数据来构建预测模型,其中每个训练样本都有其对应的真值输出.尽管现有的技术已经取得了巨大的成功,但值得注意的是,由于数据标注过程的高成本,很多任务很难 ...
随机推荐
- IDEA weblogic远程调试
weblogic远程调试 这里我们使用vulhub的镜像作为初始构建镜像搭建漏洞环境 1. 搭建docker环境 新建一个目录,创建两个文件 DockerFile FROM vulhub/weblog ...
- Linux上安装服务器监视工具,名为pyDash。
pyDash – A Web Based Linux Performance Monitoring Tool 你可以通过以下命令来判断是否已安装: pip --version # Python2.x ...
- 洛谷P1583——魔法照片(结构体排序)
https://www.luogu.org/problem/show?pid=1583#sub 题目描述 一共有n(n≤20000)个人(以1--n编号)向佳佳要照片,而佳佳只能把照片给其中的k个人. ...
- 回忆之placeholder
直接看效果点这里 HTML <!DOCTYPE html> <html> <head lang="zh-CN"> <meta charse ...
- 概述 .NET 6 ThreadPool 实现
目录 前言 任务的调度 基本调度单元 IThreadPoolWorkItem 实现类的实例. Task 全局队列 本地队列 偷窃机制 Worker Thread 的生命周期管理 线程生命注入实验 .N ...
- 使用Visual Studio Code 开发 ESP8266
使用Visual Studio Code 开发 ESP8266 ESP8266+ArduinoIDE+VSCode开发ESP8266. 首先说明一下ESP8266并不是某一WiFi模块的名字(我以前是 ...
- 对象赋值在PHP中到底是不是引用?
之前的文章中,我们说过变量赋值的问题,其中有一个问题是对象在进行变量赋值的时候,直接就是引用赋值.那么到底真实情况是怎样呢? 之前变量赋值的文章 PHP的变量赋值 对象引用测试 在继续深入的学习PHP ...
- Nginx系列(4)- Nginx安装 | Windows
下载 访问官网,选择稳定版对应的Windows系列 安装解压即可 启动nginx 有很多种方法启动nginx 直接双击nginx.exe,双击后一个黑色的弹窗一闪而过 打开cmd命令窗口,切换到ngi ...
- Docker系列(26)- 发布镜像到阿里云容器服务
1.登录阿里云 2.找到容器镜像服务 3.创建命名空间 4.创建镜像仓库 5.上传镜像
- django class类即视图类添加装饰器的几种方法
根据别人发布整理,个人爱好收集(原文:https://blog.csdn.net/mydistance/article/details/83958655 ) 第一种:定义函数装饰器,在函数,类中使用函 ...




