关于一些基础的dp——硬币的那些事（dp的基本引入）

1.最少硬币问题大体题意：

有n种硬币，面值分别是v1,v2......vn，数量无限，输入一个非负整数s，选用硬币使其和为s，要求输出最少的硬币组合。

我们可以这样分析：

定义一个名为Min[s]的数组来表示是金额s所对应的最少硬币的组合，所以对我们来说，只要是在程序中查到Min[i]的大小就可以知道最少的硬币组合是多少了。

以面值为{1，5，10，25，50}为例子来讲一下，方便以后备赛。

假如我们输入的s是100，当全用1coin的时候，如图：(画的很拙劣，抱歉）

那么第一个格子里指的就是当金额为0的时候所需要的硬币数是0，那当金额为1的时候Min[1]=Min[1-1]+1，以此类推,当然，这是只使用硬币面值为1的时候。

当我们加入了面值5，就变成了这样子：

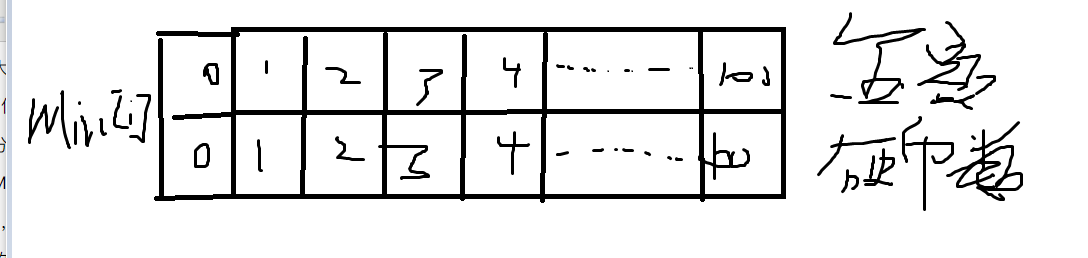
我们可以看到，到了5的时候，选择就变成了两种——一个是5个1元的硬币，另一个是直接一个5元的硬币，可以这么理解：

Min[5]=min(Min[5],Min[5-5]+1),这样才能保证硬币数是最小的。

我们还有其他面值的硬币，当然也要一一的引入。

所以说，我们在dp中将Min[i]这种记录问题最优解的数据叫做“状态”，从Min【i-1】，Min【i-5】这种式子叫做状态转移，在问题中，我们可以清晰的看见动态规划往往是利用问题前面的状态，也就是利用子问题的关联性去解决问题，这是dp的一大特点。

本题题解如下：

 1 #include<bits/stdc++.h>
 2  using namespace std;
 3  int Min[251];//每个金额所对应的最少的硬币数
 4  int coin[5]={1,5,10,25,50};//5种金额
 5  int Min_path[251]={0};
 6  void ans()
 7  {
 8      for(register int k=0;k<251;k++)
 9      Min[k]=INT_MAX;//定义初始值是无穷大
10      Min[0]=0;
11      for(register int j=0;j<5;j++)
12
13          for(register int i=coin[j];i<251;i++)
14          {
15              Min_path[i]=coin[j];
16              Min[i]=min(Min[i],Min[i-coin[j]]+1);
17         }
18 }
19 /*void print_ans(int *coin_path,int s)//打印组合
20 {
21     while(s)
22     {
23         cout<<Min_path[s]<<' ';
24         s=s-Min_path[s];
25     }
26 }*/
27  int main()
28 {
29     ios::sync_with_stdio(false);
30     int s;
31     ans();//打表
32     cin>>s;
33     cout<<Min[s]<<endl;
34     //print_ans(Min_path,s);
35      return 0;
36 } 

但是对于所有硬币问题，就不能这么解了。

2.所有硬币问题大体题意如下（HDUOJ2069，但是HDUOJ进不去了）：

有n种硬币，面值依旧是前面那些巴拉巴拉，到最后就不一样了，要求输出所有硬币组合。

我们这一局采用dp来解，用dp[i][j]来表示当金额为i的时候最少需要j枚硬币。

dp[0][0]是0，那dp[1][1]就是dp[1-1][1-1]+1,画图表示一下：

那我们可以一次类推dp[i][j]=min(dp[i][j],dp[i-coin[k]][j-1]

可以看到，dp[i][j]纵坐标的结果相加就是最少硬币的组合。

代码如下：

 1 #include<bits/stdc++.h>
 2  using namespace std;
 3  int ans[251];
 4  int coin[5]={1,5,10,25,50};
 5  int dp[251][101];
 6  void solve()
 7  {
 8      dp[0][0]=1;//0元0个硬币算是一种方案
 9      for(int i=0;i<5;i++)
10      {
11          for(int j=1;j<101;j++)//硬币数不超过100
12          {
13              for(int k=coin[i];k<251;k++)
14              {
15                  dp[k][j]+=dp[k-coin[i]][j-1];
16             }
17         }
18     }
19  }
20  int main()
21  {
22      int s;
23      solve();
24     cin>>s;
25     for(int i=0;i<251;i++)
26     {
27         for(int j=0;j<101;j++)
28         {
29             ans[i]+=dp[i][j];
30         }
31     }
32     cout<<ans[s]<<endl;
33  }

这就是基础的dp引入，硬币问题就解决了。

sdutoj

有一个最少硬币问题：https://acm.sdut.edu.cn/onlinejudge3/problems/1725?from=%2Fsets%2F17

但这个就不是dp的简单引入了，这个属于多重背包啦~~~