上手Coc.nvim 完全指南

介绍

Coc.nvim 是一个基于NodeJS 的适用于Vim8, Neovim 的Vim 智能补全插件。

拥有完整的LSP 支持。配置、使用方式及插件系统的整体风格类似 VSCode.

对于我自己来说，选择它的原因就是它安装简单，功能够用。相比YouCompleteMe 而言安装过程简直太舒服了。

更多的信息可以参见Wiki.

另：因为Coc 本身是Vim 的一个插件而已，但它又有自己的插件系统，所以下面我会将Coc 的插件叫做子插件以作区分。

安装

前提

因为Coc.nvim 是基于NodeJS 的，所以如果机器上没有NodeJS 需要先安装NodeJS.

Vundle

添加下面的内容到.vimrc:

Plugin 'neoclide/coc.nvim'

在Vim 里面运行以下命令：

:source %

:PluginInstall

Vundle 版本低于0.10.2 的将Plugin 替换成Bundle.

NeoBundle

添加下面的内容到.vimrc:

NeoBundle 'neoclide/coc.nvim'

在Vim 里面运行以下命令：

:source %

:NeoBundleInstall

VimPlug

添加下面的内容到.vimrc:

Plug 'neoclide/coc.nvim'

在Vim 里面运行以下命令：

:source %

:PlugInstall

Pathogen

切换到Pathogen 目录下并拉对应仓库即可：

cd ~/.vim/bundle

git clone https://github.com/neoclide/coc.nvim

添加插件

因为Coc 本身并不提供具体语言的补全功能，更多的只是提供了一个补全功能的平台，

所以在安装完成后，我们需要安装具体的语言服务以支持对应的补全功能。

打开Vim 并使用以下命令即可自动安装子插件及相关依赖。

:CocInstall coc-json coc-tsserver

其中coc-json coc-tsserver 这些是对应的支持JSON, Typescript 的相关子插件。

要检索都有哪些子插件可以直接在Npm 上查找coc.nvim,

亦或者使用coc-marketplace 直接在Vim 里面进行管理，安装命令如下：

:CocInstall coc-marketplace

安装完后用下面命令可以打开面板，Tab 可对高亮的子插件进行安装卸载等操作。

# 打开面板

:CocList marketplace

# 搜索python 相关子插件

:CocList marketplace python

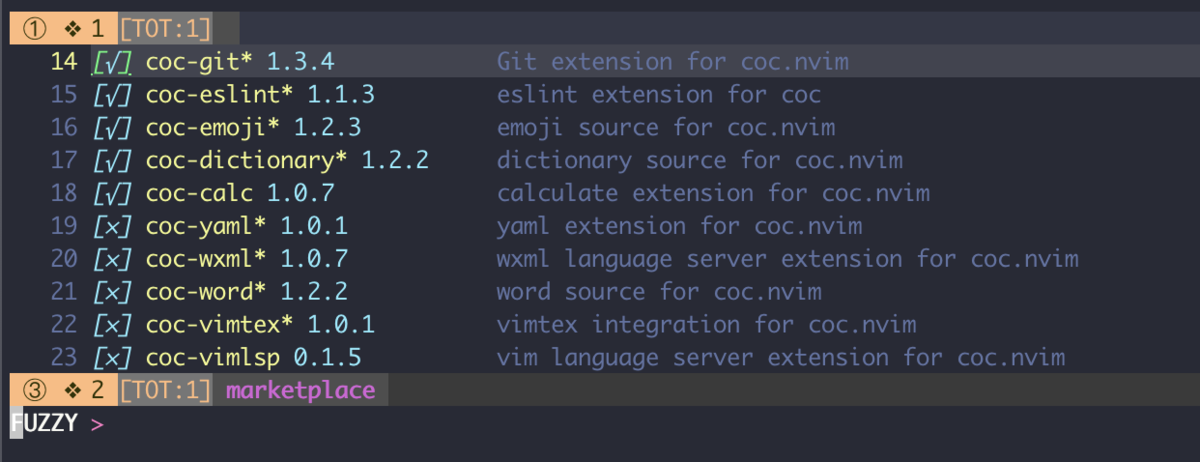
用上下可以选择，按Tab 可以进行对应操作。

另外在这里有一份相对完整的已支持的子插件列表，但不确定是否全面。

修改配置

在Vim 中可以对各个内置的功能或者外加的子插件进行配置。就类似Vscode 的配置系统一样。具体可以设置什么内容可以参见仓库的Wiki

我自己用的不多，只添加了coc-prettier 相关的几个：

{

  "prettier.singleQuote": true,

  "prettier.trailingComma": "all",

  "prettier.bracketSpacing": false

}

在 ~/.vimrc 中添加以下内容，可以使用Tab 和 Shift+Tab 进行选择补全。

" Use <Tab> and <S-Tab> to navigate the completion list

inoremap <expr> <Tab> pumvisible() ? "\<C-n>" : "\<Tab>"

inoremap <expr> <S-Tab> pumvisible() ? "\<C-p>" : "\<S-Tab>"

添加常用快捷键

为一些常用的功能添加快捷键，可以在 ~/.vimrc 中写入：

" Use <Ctrl-F> to format documents with prettier

command! -nargs=0 Prettier :CocCommand prettier.formatFile

noremap <C-F> :Prettier<CR>

上面这段配置添加了一个Prettier 的快捷命令 :Prettier 并添加了快捷键Ctrl+F.