分组密码（四）AES算法① — 密码学复习（七）

介绍完S-PN型结构之后，下面介绍AES算法。由于内容比较多所以将其分为两篇来介绍，本篇主要讲AES的历史时间节点、产生背景、与DES的对比、算法框图（粗略）以及一些数学基础。

7.1 AES的历史时间节点及产生背景

7.1.1 AES的历史时间节点

1997年，美国政府(NIST)向社会公开征集高级数据加密标准(AES):

第一轮：1998年8月20日从应征的21个算法中选出15个算法。

第二轮：1999年8月又选中其中5个算法。

第三轮：2000年10月2日再选出1个算法。

2001年11月26日，NIST接受其为标准。

7.1.2 AES的产生背景

① 1984年12月，里根总统下令由国家安全局(NSA)研制新密码标准，以取代DES.

② 1991年新密码开始试用并征求意见。但其有如下特点：

·不公开算法，只提供芯片；

·新密码设计成双刃剑，它是安全的。但通过法律允许可破译监听；

·民众要求公开算法，并去掉法律监督。

③ 1994年，颁布新密码标准EES.

④ 1995年5月，贝尔实验室博士生M.Blaze在PC机上用45分钟攻击法律监督字段获得成功。

⑤ 1995年7月，美国政府放弃用EES加密数据。

⑥ 1997年，美国政府向社会公开征集AES.

⑦ 从DES到AES反映了美国商用密码政策的变化。

公开征集DES（成功） -> 秘密设计EES（不成功） -> 公开征集AES（成功）

这说明：① 商用密码应当坚持公开设计、公布算法的政策，这是商用密码的客观规律。

② 群众的力量是伟大的。

7.1.3 AES的设计要求

① 安全性：可以抵抗目前所有的已知攻击。

② 实用性：适应各种应用环境，加解密速度快。

③ 扩展性：分组长度和密钥长度可扩展，可以适应社会对保密性不断提高的需求。

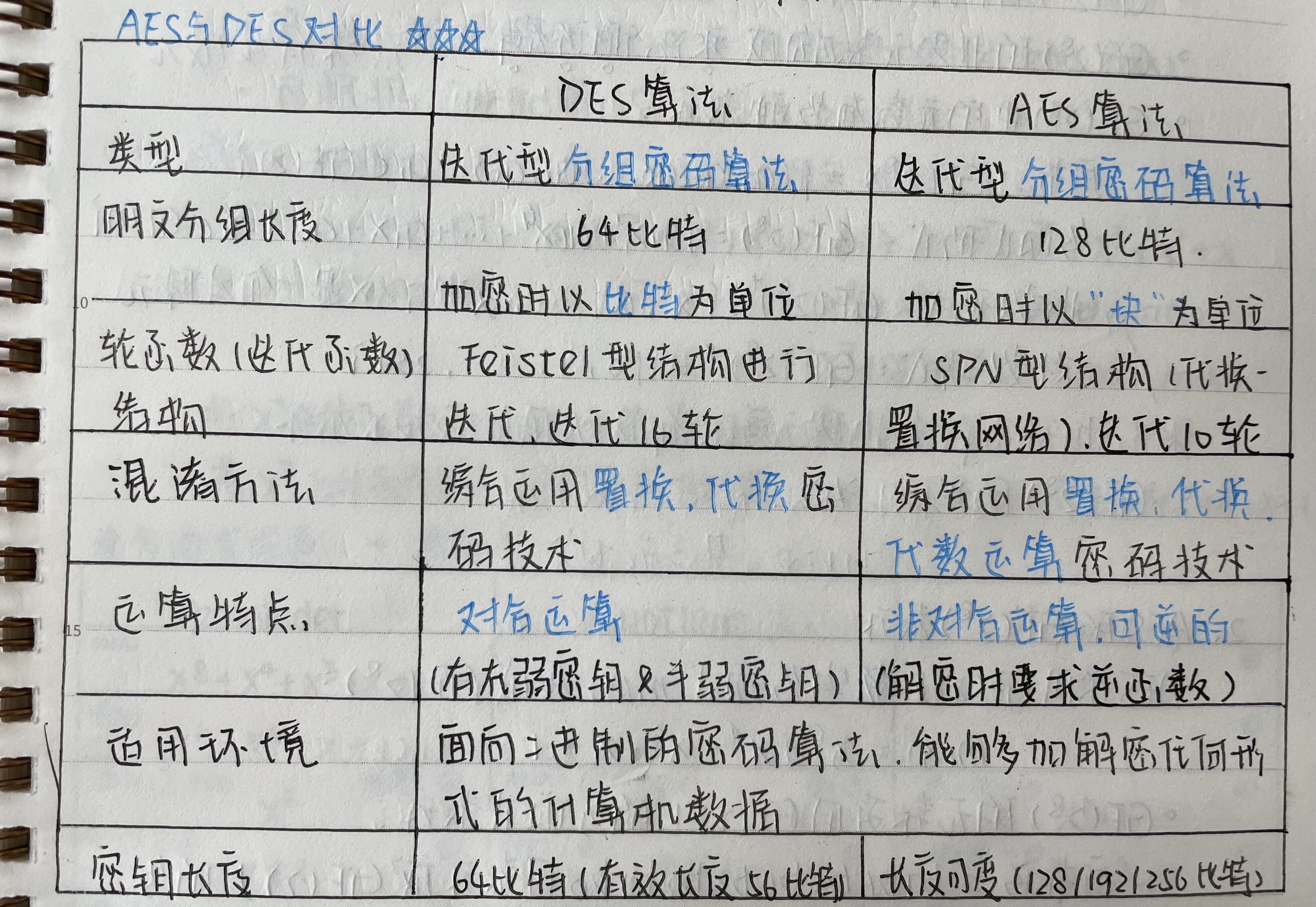
7.2 AES与DES的对比

在讲述具体的算法之前，让我们来看一下AES和DES的对比。

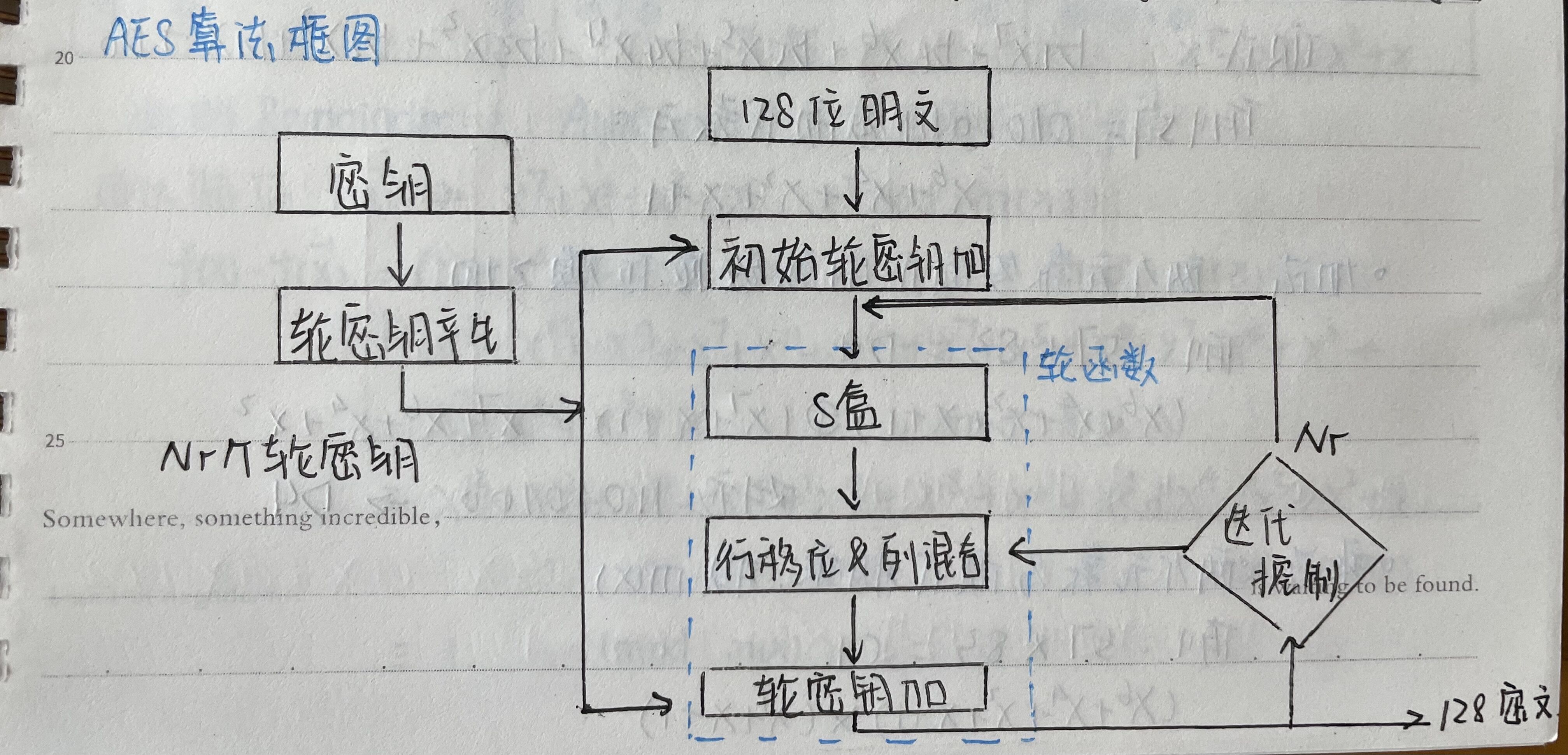
7.3 AES算法框图

接下来让我们看一下AES算法的框图，可以看到AES算法中也有S盒，但要注意这里的S盒和DES算法中的S盒并不一样，具体内容将在后面详细阐述。

7.4 数学基础

由于AES中涉及到一些计算需要一些简单的数学基础，下面将对其进行简单讲解。

7.4.1 AES的基础域是有限域GF(2⁸)

一个字节的全体256种取值构成一个GF(2⁸)
一个GF(2)上的8次既约多项式可以生成一个GF(2⁸)
GF(2⁸)的全体元素构成加法交换群
GF(2⁸)的非零元素构成乘法交换群（这意味着有生成元）
GF(2⁸)中的元素有多种表示：

字节：GF(2⁸)={(a₇,a₆,a₅,...,a₁,a₀)|a_i∈GF(2)}

多项式形式：GF(2⁸)={a₇x⁷+a₆x⁶+a₅x⁵+...+a₁x+a₀|a_i∈GF(2)}

指数形式：GF(2⁸)^*={α⁰,α¹,...,α²⁵⁴},α是一个本原元。（去掉零元素是乘法循环群，其余元素都可以用生成元来表示）

对数形式：GF(2⁸)^*={0,1,2,...,254}

GF(2⁸)的特征为2.

7.4.2 AES的GF(2⁸)表示

AES采用GF(2)上既约多项式m(x)生成GF(2⁸)：

m(x)=x⁸+x⁴+x³+x+1

GF(2⁸)的元素采用GF(2)上的多项式表示：

字节B=b₇b₆b₅b₄b₃b₂b₁b₀可表示成GF(2)上的多项式：b₇x⁷+b₆x⁶+b₅x⁵+b₄x⁴+b₃x³+b₂x²+b₁x+b₀.

例：57 = 0101 0111 多项式表示为：x⁶+x⁴+x²+x+1.

加法：两个元素多项式的系数按位模2加

例：57 + 83 = D4

（x⁶+x⁴+x²+x+1）+（x⁷+x+1） = x⁷+x⁶+x⁴+x²

而x⁷+x⁶+x⁴+x²对应1101 0100，即D4.

乘法：两个元素多项式相乘，模m(x)

例：57 × 83 = C1

（x⁶+x⁴+x²+x+1）×（x⁷+x+1） = x¹³+x⁷+x⁶+x¹¹+x⁵+x⁴+x⁹+x³+x²+x⁸+x²+x+x⁷+x+1

= x¹³+x¹¹+x⁹+x⁸+x⁶+x⁵+x⁴+x³+1

= x⁷+x⁶+1 mod x⁸+x⁴+x³+x+1

乘法单位元：字节01 多项式表示为：1
乘法逆元

设a(x)的逆元为b(x)，则a(x)b(x)=1 mod m(x)

可根据Euclid算法可求出b(x).

x乘法xtime：用x乘GF(2⁸)的元素

例：xtime(57) = x (x⁶+x⁴+x²+x+1) = x⁷+x⁵+x³+x²+x

xtime(83) = x（x⁷+x+1）= x⁸+x²+x mod m(x) = x⁷+x⁴+x³+1

若x⁷的系数为0，则为简单相乘，系数左移；若x⁷的系数为1，则乘后取模m(x)，即乘后减去x⁸+x⁴+x³+x+1.

多项式求逆

下面通过一个例子来说明多项式求逆的方法：

在求解后还可以将两者相乘看结果是否mod m(x)与1同余，如果是则所求结果正确。这个写法是参考：手动推导计算AES中的s盒的输出。

7.4.3 AES的字表示与运算

AES数据处理单位是字节和字。

一个字 = 4个字节 = 32比特

一个字可以表示为系数取自GF(2⁸)上的次数低于4次的多项式。

例：字 57 83 4A D1 -> 57x³+83x²+4Ax+D1

字加法：两多项式系数按位模2加（不进位）

例：(57x³+83x²+4Ax+D1)+(Ax³+B3x²+EF)=5Dx³+30x²+4Ax+3F.

字乘法：设a和c是两个字，a(x)和c(x)是其字多项式。AES定义a和c的乘积b为

b(x) = a(x)c(x) mod x⁴+1

设：a(x)=a₃x³+a₂x²+a₁x+a₀

c(x)=c₃x³+c₂x²+c₁x+c₀

b(x)=b₃x³+b₂x²+b₁x+b₀

则 b(x) = a(x)c(x) mod x⁴+1为：

b₀= a₀c₀+a₃c₁+a₂c₂+a₁c₃

b₁= a₁c₀+a₀c₁+a₃c₂+a₂c₃

b₂= a₂c₀+a₁c₁+a₀c₂+a₃c₃

b₃= a₃c₀+a₂c₁+a₁c₂+a₀c₃

写成矩阵的形式：

注意：①x⁴+1是可约多项式，字c(x)不一定有逆。

②但AES选择的c(x)有逆，c(x)=03x³+01x²+01x+02.(0多1少，速度快)

③c(x)有逆的条件是(x⁴+1,c(x))=1

字的x乘法：设b(x)是一个字，p(x)=xb(x) mod x⁴+1

写成矩阵的形式：

注意：因为模x⁴+1，字的x乘法相当于按字节循环移位。

7.4.4 AES的数据处理方式

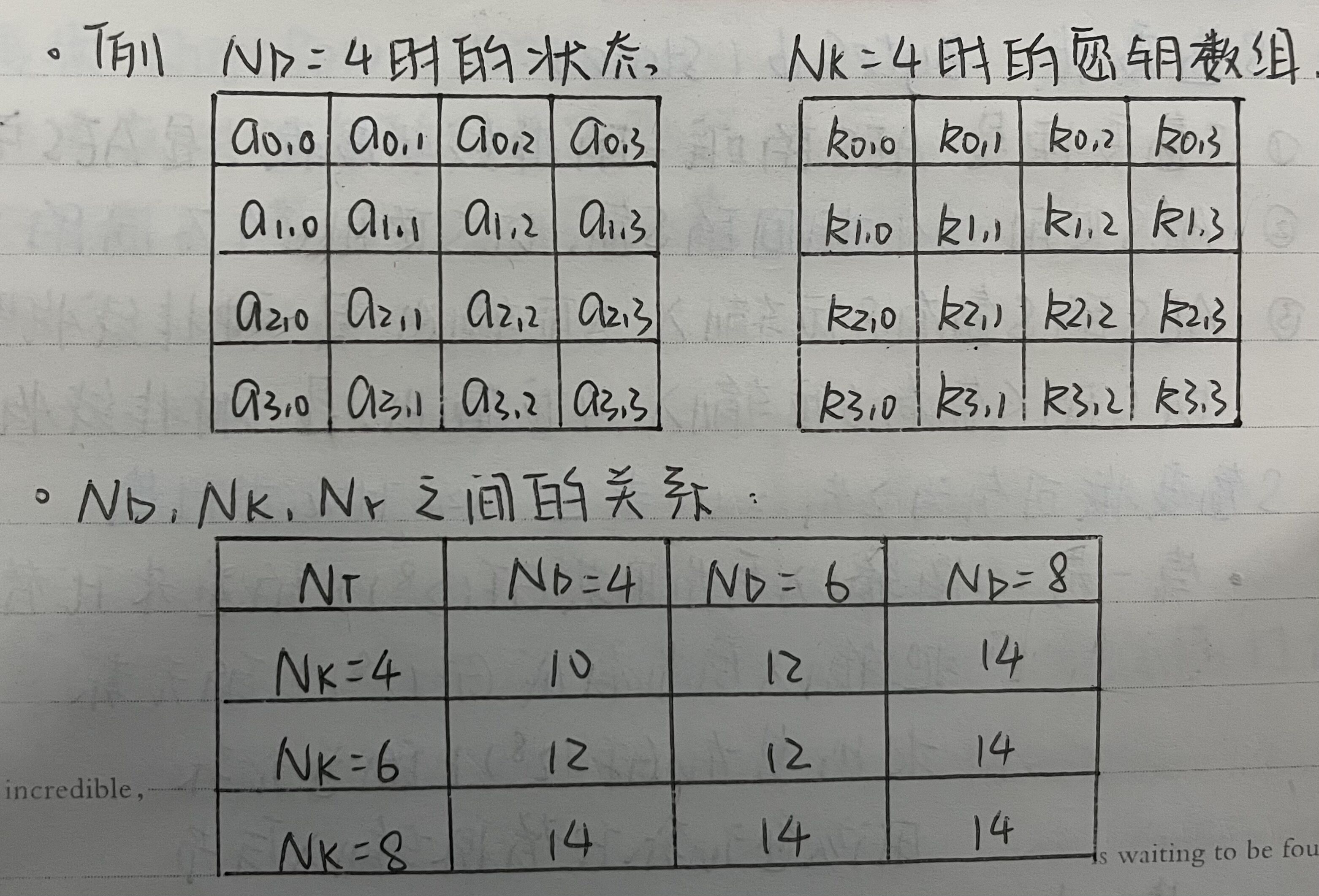
AES的数据处理方式有：按字节处理、按字处理和按状态处理。

状态：

加解密过程中的中间数据
以字节为元素的矩阵或二维数组
符号：Nb——明密文所含的字数；Nk——密钥所含的字数；Nr——迭代轮数。

参考博客：

[1] 手动推导计算AES中的s盒的输出