Atcoder Grand Contest 024 E - Sequence Growing Hard（dp+思维）

题目传送门

典型的 Atcoder 风格的计数 dp。

题目可以转化为每次在序列中插入一个 \([1,k]\) 的数，共操作 \(n\) 次，满足后一个序列的字典序严格大于前一个序列，问有多少种操作序列。

显然相同的数可以合并，因为在由相同的数 \(x\) 组成的数段中，在任何位置插入 \(x\)，得到的序列都是相同的。

再考虑字典序的问题。你只能序列末尾或者一个 \(<x\) 的数前面插入 \(x\)，否则得到的序列的字典序就会 \(\geq\) 原序列的字典序。

但这样问题还是比较棘手，我们还需进一步转化。

我们把操作序列转化为一棵有根树，树上每个节点都是一个二元组 \((val,dfn)\)，表示第 \(dfn\) 次操作插入了值为 \(val\) 的数。如果第 \(i\) 次操作将 \(v\) 插在第 \(j\) 次操作插入的数 \(w\) 前面，那么我们就将节点 \((v,i)\) 挂在 \((w,j)\) 下面。新建一个虚拟节点 \((0,0)\)，如果在序列末尾插入 \(v\)，那么就把 \((v,i)\) 挂在 \((0,0)\) 下面。

由于我们只能在 \(<x\) 的数前面插入 \(x\)，因此若 \(y\) 为 \(x\) 的父亲，那么 \(val_y>val_x\)，\(dfn_y<dfn_x\)

不妨举个例子，假设有如下的操作序列：

1. 向序列中插入数 \(1\)，得到序列 \([1]\)。这可看成将点 \((1,1)\) 挂在点 \((0,0)\) 下面。
2. 在 \(1\) 前插入 \(3\)，得到序列 \([3,1]\)。这可看成将点 \((3,2)\) 挂在点 \((1,1)\) 下面。
3. 在序列末尾插入 \(2\)，得到序列 \([3,1,2]\)。这可看成将点 \((2,3)\) 挂在点 \((0,0)\) 下面。
4. 在 \(1\) 再插入一个 \(3\)，得到序列 \([3,3,1,2]\)。这可看成将点 \((3,4)\) 挂在点 \((1,1)\) 下面。
5. 在 \(1\) 前插入一个 \(2\)，得到序列 \([3,3,2,1,2]\)。这可看成将点 \((2,5)\) 挂在点 \((1,1)\) 下面。
6. 在第二个 \(3\) 前插入一个 \(4\)，得到序列 \([3,4,3,2,1,2]\)。这可看成将点 \((4,6)\) 挂在点 \((3,4)\) 下面。

这样 \(6\) 次操作下来，我们得到了一棵 \(7\) 个节点的树，如下图：



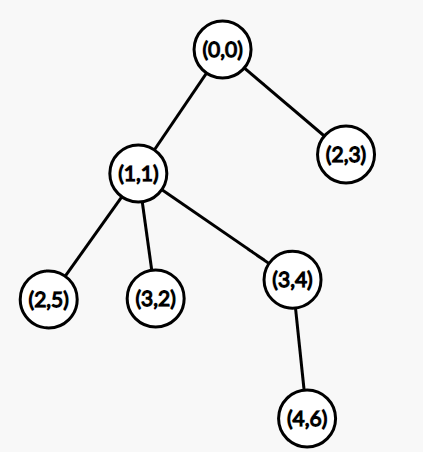
一种操作序列恰对应一棵树，一棵满足条件的树也对应一种操作序列。因此问题转化为有多少个满足条件的树。

这就可以直接 \(dp\) 了。我们设 \(dp_{i,j}\) 表示有多少个以 \(i\) 为节点的树，根节点的 \(val\) 为 \(j\)。

考虑转移，对于 \(i>1\)，假设根节点的 \(dfn\) 为 \(1\)，那么根节点必定有个儿子，其 \(dfn\) 为 \(2\)。我们就枚举这棵子树的大小 \(l\) 和根节点的 \(val\) —— \(v\)。确定这棵子树的形态的方案数为 \(dp_{l,v}\)，将这棵子树中所有节点的 \(dfn\) 值定好的方案数为 \(C_{n-2}^{k-1}\)（从 \(3\) 到 \(n\) 这 \(n-2\) 个数中中选择 \(k-1\) 个数），填好剩余部分的方案数为 \(dp_{i-l,j}\)。因此有转移方程：

\[dp_{i,j}=\sum\limits_{l-1}^{i-1}C_{n-2}^{k-1} \times dp_{i-l,j} \times \sum\limits_{v=j+1}^k dp_{l,v}
\]

后面那个 \(\sum\) 可以用前缀和优化掉。时间复杂度 \(\mathcal O(n^2k)\)

/*
Contest: -
Problem: Atcoder Grand Contest 024 E
Author: tzc_wk
Time: 2020.7.22
*/
#include <bits/stdc++.h>
using namespace std;
#define fi			first
#define se			second
#define fz(i,a,b)	for(int i=a;i<=b;i++)
#define fd(i,a,b)	for(int i=a;i>=b;i--)
#define foreach(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define all(a)		a.begin(),a.end()
#define fill0(a)	memset(a,0,sizeof(a))
#define fill1(a)	memset(a,-1,sizeof(a))
#define fillbig(a)	memset(a,0x3f,sizeof(a))
#define fillsmall(a) memset(a,0xcf,sizeof(a))
#define y1			y1010101010101
#define y0			y0101010101010
#define int long long
typedef pair<int,int> pii;
inline int read(){
	int x=0,neg=1;char c=getchar();
	while(!isdigit(c)){
		if(c=='-')	neg=-1;
		c=getchar();
	}
	while(isdigit(c))	x=x*10+c-'0',c=getchar();
	return x*neg;
}
int n=read(),k=read(),m=read();
int C[305][305],s[305][305],dp[305][305];
signed main(){
	fz(i,0,300){
		C[i][0]=1;
		fz(j,1,i)	C[i][j]=(C[i-1][j]+C[i-1][j-1])%m;
	}
//	printf("%d\n",C[5][3]);
	fz(i,0,k)	dp[1][i]=1;
	fd(i,k,0)	s[1][i]=(s[1][i+1]+dp[1][i])%m;
	fz(i,2,n+1){
		fz(j,0,k)
			fz(l,1,i-1)
				dp[i][j]=(dp[i][j]+C[i-2][l-1]*dp[i-l][j]%m*s[l][j+1]%m)%m;
		fd(j,k,0)	s[i][j]=(s[i][j+1]+dp[i][j])%m;
	}
	printf("%lld\n",dp[n+1][0]);
	return 0;
}