Solution -「JSOI 2019」「洛谷 P5334」节日庆典

\(\mathscr{Description}\)

  Link.

  给定字符串 \(S\)，求 \(S\) 的每个前缀的最小表示法起始下标（若有多个，取最小的）。

  \(|S|\le3\times10^6\)。

\(\mathscr{Solution}\)

  注意到一个显然的事实，对于某个前缀 \(S[:i]\) 以及两个起始下标 \(p,q\)，若已有 \(S[p:i]<S[q:i]\)，那么在所有的 \(j>i\) 中，都有 \(S[p:j]<S[q:j]\)。换言之，最终 \(i\) 的答案 \(r_i\) 必然满足 \(r_i\in B_i=\arg\min_{p\le i}\{S[p:i]\}\)，同时有 \(B_{i+1}\subseteq B_i\cup\{i+1\}\)，故我们可以通过去除 \(B_i\cup\{i+1\}\) 中不优秀的起始位置来得到 \(B_{i+1}\)。

  可惜，\(|B_m|=\mathcal O(m)\) 的，需要进一步精简。这提示我们反思“\(S[p:i]\) 取最小”是否是“\(p\) 可能成为 \(r_i\)”的充要条件。答案是否定的。考虑后缀 \(S[p:i]\) 和 \(S[q:i]~(p<q)\)，若 \(p,q\in B_i\)，有 \(S[p:p+i-q+1]=S[q:i]\)，即 \(S[q:i]\) 是 \(S[p:i]\) 的一个 border。由 border 的相关性质，自然地想到研究 \(|S[q:i]|>\frac{|S[p:i]|}{2}\) 的情况，此时 \(S[p:i]\) 有周期 \(T=|S[p:i]|-|S[q:i]|\)。取 \(S[r:i]=S[i-T+1:i]\)，可以说明：\(S[p:i]\) 不同时大于 \(S[q:i]\) 和 \(S[r:i]\)。如图：

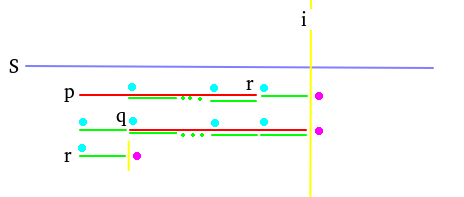
  若我们想让 \(S[p:i]<S[q:i]\)，就需要在后缀加一个字符 \(S_{i+1}=x\)（红点），使得 \(x>y\)（蓝点），但一旦有 \(y<x\)，就能让最后一个周期 \(S[r:i]\) 带上红点一路走到 \(S[p:i]\) 的开头，得到 \(S[r:i+1]<S[p:i+1]\)，故结论成立。 \(\square\)

  据此维护出不存在满足上述 \(p,q\) 关系的新集合 \(B_i'\subseteq B_i\)，显然 \(|B_m'|=\mathcal O(\log m)\)，所以维护总过程是 \(\mathcal O(n\log n)\) 的。

  此外，求答案 \(r_i\) 时，仍然有必要枚举 \(B_i'\) 中的每个下标取优。利用前缀相等的性质，发现我们仅需要完成 \(S\) 子串与 \(S\) 前缀的快速比较，那么用 Z-function 可以做到 \(\mathcal O(1)\)。综上，最终复杂度为 \(\mathcal O(n\log n)\)。

---

  这个时候就有神要问了哈，你怎么不写 \(\mathcal O(n)\) 的做法？

  重新审视一下这个问题，很自然联想到描述“最小表示法等于自身”的 Lyndon Word，而 Duval 算法提供了一个 \(\mathcal O(n)\) 考察 Lyndon Word 的思路，所以我们可以尝试把问题向 Lyndon 的方向转化。设串 \(s=S[:i]\) 的 Lyndon 分解为

\[s=w_1^{k_1}w_2^{k_2}\cdots w_m^{k_m},
\]

其中 \(w_1>w_2>\cdots>w_m\)。我们先把 \(\mathcal O(n\log n)\) 做法中的关键性结论重新描述：显然最小表示的后缀在一个 Lyndon Word 的开头，而若取出了 \(w_i^kw_{i+1}^{k_{i+1}}\cdots w_m^{k_m}\)，我们则能断言：\(k=k_i\)。

  现在套上 Duval 的样子，设 \(s=s'u^ku'\)，其中 \(u^k\) 是 Lyndon Word，\(u'\) 是 \(u\) 未扩展完的前缀。前面的 \(s'\) 也不重要了，我们记 \(t=u^ku'\) 来研究，考虑加入字符 \(c=S_{|s|+1}\)：

• \(t_{|u'|+1}<c\)，答案 \(p_{|s|+1}\) 显然为 \(t_1\) 在原串对应的下标；
• \(t_{|u'|+1}>c\)，考虑 Duval 的过程，我们得先把一段前缀循环划为 Lyndon，以后再更新 \(p_{|s|+1}\)；
• \(t_{|u'|+1}=c\)，继续吻合循环节，两种可能优解：\(p=i\) 和 \(p\) 取 \(u\) 的最优起始位置在 \(u'\) 中对应的位置。第二种情况考虑到虽然 \(u\) 为 Lyndon Word，但 \(S\) 的前缀是有可能小于 \(u\) 的后缀的。还是用上文 Z-function 的方法支持 \(\mathcal O(1)\) 比较。

  最终，与 Duval 几乎一样地，我们在 \(\mathcal O(n)\) 的时间内解决了问题。

\(\mathscr{Code}\)

• \(\mathcal O(n\log n)\):

/*+Rainybunny+*/
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)
inline void wint(const int x) {
    if (9 < x) wint(x / 10);
    putchar(x % 10 ^ '0');
}
const int MAXN = 3e6, MAXG = 100;
int n, z[MAXN + 5];
char s[MAXN + 5];
int gcnt, good[MAXG + 5]; // indices that may be the answer.
inline void calcZ() {
    z[1] = n;
    for (int i = 2, l = 0, r = 0; i <= n; ++i) {
        if (i <= r) z[i] = std::min(z[i - l + 1], r - i + 1);
        while (i + z[i] <= n && s[i + z[i]] == s[1 + z[i]]) ++z[i];
        if (i + z[i] - 1 > r) r = i + z[l = i] - 1;
    }
}
inline void adapt(const int k) {
    auto compare = [&](const int u, const int v)->int {
        return u < v ?
          (s[u + k - v] == s[k] ? 0 : s[u + k - v] < s[k] ? -1 : 1)
          : (s[k] == s[v + k - u] ? 0 : s[k] < s[v + k - u] ? -1 : 1);
    };
    static int tmp[MAXG + 5]; rep (i, 1, gcnt) tmp[i] = good[i];
    int ocnt = gcnt, pst = good[gcnt]; good[gcnt = 1] = pst;
    per (i, ocnt - 1, 1) {
        if (int t = compare(pst, tmp[i]); t > 0) {
            good[gcnt = 1] = pst = tmp[i];
        } else if (!t) {
            pst = tmp[i];
            while (gcnt && k - good[gcnt] + 1 << 1 > k - pst + 1) --gcnt;
            good[++gcnt] = pst;
        }
    }
    std::reverse(good + 1, good + gcnt + 1);
}
inline int best(const int k) {
    // compare S[l:r] with S[:r-l+1].
    auto compare = [](const int l, const int r)->int {
        if (z[l] >= r - l + 1) return 0;
        return s[l + z[l]] < s[z[l] + 1] ? -1 : 1;
    };
    int ans = good[1];
    rep (i, 2, gcnt) {
        int cur = good[i];
        if (int f1 = compare(ans + k - cur + 1, k); f1 > 0) ans = cur;
        else if (!f1) {
            int f2 = compare(cur - ans + 1, cur - 1); // cur <> ans.
            if (f2 < 0) ans = cur;
        }
    }
    return ans;
}
int main() {
    scanf("%s", s + 1), n = strlen(s + 1), calcZ();
    rep (i, 1, n) {
        good[++gcnt] = i, adapt(i);
        wint(best(i)), putchar(i < n ? ' ' : '\n');
    }
    return 0;
}

• \(\mathcal O(n)\)（目前洛谷最优解）：

/*+Rainybunny+*/
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)
inline void wint(const int x) {
    if (9 < x) wint(x / 10);
    putchar(x % 10 ^ '0');
}
const int MAXN = 3e6;
int n, z[MAXN + 5], ans[MAXN + 5];
char s[MAXN + 5];
inline void calcZ() {
    z[1] = n;
    for (int i = 2, l = 0, r = 0; i <= n; ++i) {
        if (i <= r) z[i] = std::min(z[i - l + 1], r - i + 1);
        while (i + z[i] <= n && s[i + z[i]] == s[1 + z[i]]) ++z[i];
        if (i + z[i] - 1 > r) r = i + z[l = i] - 1;
    }
}
inline void duval() {
    auto compare = [](const int u, const int v, const int k)->int {
        int p = u + k - v + 1, q = k - p + 2;
        if (z[p] < k - p + 1) {
            return s[p + z[p]] < s[1 + z[p]] ? -1 : 1;
        } else {
            return z[q] < u ? s[q + z[q]] < s[1 + z[q]] ? 1 : -1 : 0;
        }
    };
    for (int i = 1; i <= n;) {
        int j = i + 1, k = i;
        if (!ans[i]) ans[i] = i;
        while (j <= n && s[k] <= s[j]) {
            if (s[k] < s[j]) {
                if (!ans[j]) ans[j] = i;
                k = i;
            } else {
                if (!ans[j]) {
                    if (ans[k] < i) ans[j] = i;
                    else {
                        ans[j] = compare(i, j - k + ans[k], j) <= 0 ?
                          i : j - k + ans[k];
                    }
                }
                ++k;
            }
            ++j;
        }
        i += (j - i) / (j - k) * (j - k);
    }
}
int main() {
    n = fread(s + 1, 1, MAXN + 3, stdin);
    while (s[n] < 'a' || 'z' < s[n]) --n;
    calcZ(), duval();
    rep (i, 1, n) wint(ans[i]), putchar(i < n ? ' ' : '\n');
    return 0;
}