CF#335 Lazy Student

Lazy Student

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Student Vladislav came to his programming exam completely unprepared as usual. He got a question about some strange algorithm on a graph — something that will definitely never be useful in real life. He asked a girl sitting next to him to lend him some cheat papers for this questions and found there the following definition:

The minimum spanning tree T of graph G is such a tree that it contains all the vertices of the original graph G, and the sum of the weights of its edges is the minimum possible among all such trees.

Vladislav drew a graph with n vertices and m edges containing no loops and multiple edges. He found one of its minimum spanning trees and then wrote for each edge its weight and whether it is included in the found tree or not. Unfortunately, the piece of paper where the graph was painted is gone and the teacher is getting very angry and demands to see the original graph. Help Vladislav come up with a graph so that the information about the minimum spanning tree remains correct.

Input

The first line of the input contains two integers n and m (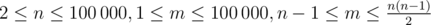) — the number of vertices and the number of edges in the graph.

Each of the next m lines describes an edge of the graph and consists of two integers aj and bj (1 ≤ aj ≤ 109, bj = {0, 1}). The first of these numbers is the weight of the edge and the second number is equal to 1 if this edge was included in the minimum spanning tree found by Vladislav, or 0 if it was not.

It is guaranteed that exactly n - 1 number {bj} are equal to one and exactly m - n + 1 of them are equal to zero.

Output

If Vladislav has made a mistake and such graph doesn't exist, print  - 1.

Otherwise print m lines. On the j-th line print a pair of vertices (uj, vj) (1 ≤ uj, vj ≤ n, uj ≠ vj), that should be connected by the j-th edge. The edges are numbered in the same order as in the input. The graph, determined by these edges, must be connected, contain no loops or multiple edges and its edges with bj = 1 must define the minimum spanning tree. In case there are multiple possible solutions, print any of them.

Sample test(s)

input

4 5
2 1
3 1
4 0
1 1
5 0

output

2 4
1 4
3 4
3 1
3 2

input

3 3
1 0
2 1
3 1

output

-1

题意：首先先取一个图的其中一个MST，给出这个图的所有边权，以及每条边是否在这个MST里。要你按照这些边权构造一个图，使得这个MST仍是你构造的那个图的其中一个MST。

分析：考虑Kruscal的过程。

不妨假设MST的边都连着1，即这些边是1-2，1-3，1-4，。。。。1-n这样连的。

那Kruscal的过程中，如果一条边不选，必定连着前面的任意两个点。

注意考虑边权相同，MST不唯一的情况。

至于某条不是MST的边如何连前面两个点，随便维护一下就好。

 /**
 Create By yzx - stupidboy
 */
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <cmath>
 #include <deque>
 #include <vector>
 #include <queue>
 #include <iostream>
 #include <algorithm>
 #include <map>
 #include <set>
 #include <ctime>
 #include <iomanip>
 using namespace std;
 typedef long long LL;
 typedef double DB;
 #define MIT (2147483647)
 #define INF (1000000001)
 #define MLL (1000000000000000001LL)
 #define sz(x) ((int) (x).size())
 #define clr(x, y) memset(x, y, sizeof(x))
 #define puf push_front
 #define pub push_back
 #define pof pop_front
 #define pob pop_back
 #define mk make_pair

 inline int Getint()
 {
     int Ret = ;
     char Ch = ' ';
     bool Flag = ;
     while(!(Ch >= '' && Ch <= ''))
     {
         if(Ch == '-') Flag ^= ;
         Ch = getchar();
     }
     while(Ch >= '' && Ch <= '')
     {
         Ret = Ret *  + Ch - '';
         Ch = getchar();
     }
     return Flag ? -Ret : Ret;
 }

 const int N = ;
 struct EdgeType
 {
     int index, value;
     bool select;
     int u, v;

     inline bool operator <(const EdgeType &t) const
     {
         if(value != t.value) return value < t.value;
         if(select ^ t.select) return select > t.select;
         return index < t.index;
     }
 } arr[N];
 typedef pair<int, int> Edge;
 priority_queue<Edge> que;
 int n, m;

 inline void Input()
 {
     n = Getint();
     m = Getint();
     for(int i = ; i < m; i++)
     {
         arr[i].value = Getint();
         arr[i].select = Getint();
         arr[i].index = i;
     }
 }

 inline bool CompareByIndex(const EdgeType &a, const EdgeType &b)
 {
     return a.index < b.index;
 }

 inline void Solve()
 {
     sort(arr, arr + m);

     int now = ;
     for(int i = ; i < m; i++)
     {
         if(arr[i].select)
         {
             arr[i].u = , arr[i].v = ++now;
             if(now > ) que.push(Edge(now, now));
         }
         else
         {
             if(que.empty())
             {
                 puts("-1");
                 return;
             }
             Edge t = que.top();
             que.pop();
             arr[i].u = --t.first, arr[i].v = t.second;
             if(t.first > ) que.push(t);
         }
     }

     sort(arr, arr + m, CompareByIndex);
     for(int i = ; i < m; i++) printf("%d %d\n", arr[i].u, arr[i].v);
 }

 int main()
 {
     freopen("a.in", "r", stdin);
     Input();
     Solve();
     return ;
 }