数据结构和算法 – 11.高级排序算法（下）

三、选择类排序

3.1.简单选择排序

http://www.cnblogs.com/tangge/p/5338734.html#XuanZe

3.2 堆排序
要知道堆排序，首先要了解一下二叉树的模型。

下图就是一颗二叉树

那么堆排序中有两种情况（看上图理解）：

    大根堆：  就是说父节点要比左右孩子都要大。

    小根堆：  就是说父节点要比左右孩子都要小。

那么要实现堆排序,必须要做两件事情：

第一：构建大根堆。

首先这是一个无序的堆，那么我们怎样才能构建大根堆呢？

     第一步： 首先我们发现，这个堆中有2个父节点(2,3);

     第二步： 比较2这个父节点的两个孩子（4，5），发现5大。

     第三步： 然后将较大的右孩子（5）跟父节点（2）进行交换，至此3的左孩子堆构建完毕，

第四步： 比较第二个父节点（3）下面的左右孩子（5，1），发现左孩子5大。

第五步： 然后父节点（3）与左孩子（5）进行交换，注意，交换后，堆可能会遭到破坏，

           必须按照以上的步骤一，步骤二，步骤三进行重新构造堆。

 

最后构造：

 

第二：输出大根堆。

             至此，我们把大根堆构造出来了，那怎么输出呢？我们做大根堆的目的就是要找出最大值，

         那么我们将堆顶（5）与堆尾（2）进行交换，然后将（5）剔除根堆，由于堆顶现在是（2），

         所以破坏了根堆，必须重新构造，构造完之后又会出现最大值，再次交换和剔除，最后也就是俺们

         要的效果了。

///<summary>
        /// 构建堆
        ///</summary>
        ///<param name="list">待排序的集合</param>
        ///<param name="parent">父节点</param>
        ///<param name="length">输出根堆时剔除最大值使用</param>
        public static void HeapAdjust(List<int> list, int parent, int length)
        {
            //temp保存当前父节点
            int temp = list[parent];

            //得到左孩子(这可是二叉树的定义哇)
            int child = 2 * parent + 1;

            while (child < length)
            {
                //如果parent有右孩子，则要判断左孩子是否小于右孩子
                if (child + 1 < length && list[child] < list[child + 1])
                    child++;

                //父节点大于子节点，不用做交换
                if (temp >= list[child])
                    break;

                //将较大子节点的值赋给父亲节点
                list[parent] = list[child];

                //然后将子节点做为父亲节点，已防止是否破坏根堆时重新构造
                parent = child;

                //找到该父节点左孩子节点
                child = 2 * parent + 1;
            }
            //最后将temp值赋给较大的子节点，以形成两值交换
            list[parent] = temp;
        }

        ///<summary>
        /// 堆排序
        ///</summary>
        ///<param name="list">待排序的集合</param>
        ///<param name="top">前K大</param>
        ///<returns></returns>
        public List<int> HeapSort(List<int> list, int top)
        {
            //string joinlist = string.Join(",", list.ToList());
            List<int> topNode = new List<int>();

            //list.Count/2-1:就是堆中非叶子节点的个数
            for (int i = list.Count / 2 - 1; i >= 0; i--)
            {
                HeapAdjust(list, i, list.Count);
                //joinlist = string.Join(",", list.ToList());
            }

            //最后输出堆元素（求前K大）
            for (int i = list.Count - 1; i >= list.Count - top; i--)
            {
                //堆顶与当前堆的第i个元素进行值对调
                int temp = list[0];
                list[0] = list[i];
                list[i] = temp;
                //joinlist = string.Join(",", list.ToList());
                //最大值加入集合
                topNode.Add(temp);

                //因为顺序被打乱，必须重新构造堆
                HeapAdjust(list, 0, i);
                //joinlist = string.Join(",", list.ToList());
            }
            return topNode;
        }

List<int> list1 = new List<int>();
            int[] array1 = new int[] { 20, 40, 50, 10, 60 };
            list1.AddRange(array1);
            new QuickSortClass().HeapSort(list1, 5);

            Console.WriteLine("堆排序：");
            Console.Write(string.Join(",", list1.ToList()));

 

总结：堆排序的执行时间主要由建立初始堆和反复调整堆这两个部分的时间开销组成，由于堆排序对原始记录的排序状态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为O(nlog₂n)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n²)的时间复杂度了。另外，由于初始构建堆所需的比较次数较多，因此，它并不适合待排序序列个数较少的情况。

四、归并类排序

4.1 二路归并排序介绍

4.2 二路归并排序实现

 

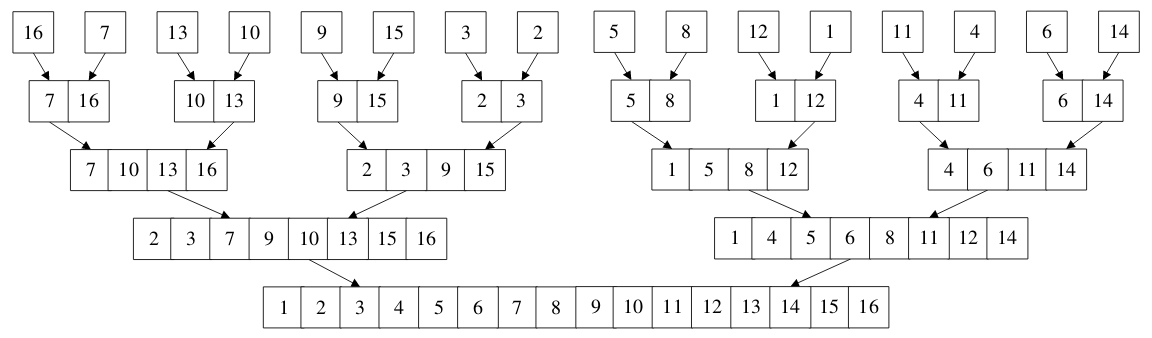
总结：

（1）当待排序序列的记录数n较小的时候（一般n<=50），可以采用直接插入排序、直接选择排序或冒泡排序：

若序列初始状态基本为正序，则应选用直接插入排序、冒泡排序。

如果单条记录本身信息量较大，由于直接插入排序所需的记录移动操作较直接选择排序多，因此用直接选择排序较好。

（2）当待排序序列的记录数n较大的时候，则应采用时间复杂度为O(nlog₂n)的排序方法，如：快速排序、堆排序或归并排序。

快速排序时目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字随机分布时，快速排序的平均时间最短，.NET中集合类的内置排序方法（例如：Array.Sort()）也是使用了快速排序实现的。

堆排序需要的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况O(n²)。

归并排序需要大量的辅助空间，因此不值得提倡使用，但是如果要将两个有序序列组合成一个新的有序序列，最好的方法就是归并排序。