逻辑回归模型(Logistic Regression, LR)--分类

逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。本文主要详述逻辑回归模型的基础，至于逻辑回归模型的优化、逻辑回归与计算广告学等，请关注后续文章。

1 逻辑回归模型

回归是一种极易理解的模型，就相当于y=f(x)，表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切，之后判定病人是否生病或生了什么病，其中的望闻问切就是获取自变量x，即特征数据，判断是否生病就相当于获取因变量y，即预测分类。

最简单的回归是线性回归，在此借用Andrew NG的讲义，有如图1.a所示，X为数据点——肿瘤的大小，Y为观测值——是否是恶性肿瘤。通过构建线性回归模型，如hθ (x)所示，构建线性回归模型后，即可以根据肿瘤大小，预测是否为恶性肿瘤h θ (x)≥.05为恶性，h θ (x)<0.5为良性。

然而线性回归的鲁棒性很差，例如在图1.b的数据集上建立回归，因最右边噪点的存在，使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致，而分类范围，需要在[0,1]。逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型，其回归方程与回归曲线如图2所示。逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为(0,1)。

图2 逻辑方程与逻辑曲线

逻辑回归其实仅为在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，逻辑回归成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。对于多元逻辑回归，可用如下公式似合分类，其中公式(4)的变换，将在逻辑回归模型参数估计时，化简公式带来很多益处，y={0,1}为分类结果。

对于训练数据集，特征数据x={x 1 , x 2 , … , x m }和对应的分类数据y={y 1 , y 2 , … , y m }。构建逻辑回归模型f(θ)，最典型的构建方法便是应用极大似然估计。首先，对于单个样本，其后验概率为：

那么，极大似然函数为：

log似然是：

2 梯度下降

由第1节可知，求逻辑回归模型f(θ)，等价于：

采用梯度下降法：

从而迭代θ至收敛即可：

3 模型评估

对于LR分类模型的评估，常用AUC来评估，关于AUC的更多定义与介绍，可见参考文献2，在此只介绍一种极简单的计算与理解方法。

对于训练集的分类，训练方法1和训练方法2分类正确率都为80%，但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中，5和6两数据分类错误，但这两个数据位于分类面附近，而训练方法2中，将10和1两个数据分类错误，但这两个数据均离分类面较远。

AUC正是衡量分类正确度的方法，将训练集中的label看两类{0，1}的分类问题，分类目标是将预测结果尽量将两者分开。将每个0和1看成一个pair关系，团中的训练集共有5*5=25个pair关系，只有将所有pair关系一至时，分类结果才是最好的，而auc为1。在训练方法1中，与10相关的pair关系完全正确，同样9、8、7的pair关系也完全正确，但对于6，其pair关系(6，5)关系错误，而与4、3、2、1的关系正确，故其auc为(25-1)/25=0.96；对于分类方法2，其6、7、8、9的pair关系，均有一个错误，即(6,1)、(7,1)、(8,1)、(9,1)，对于数据点10，其正任何数据点的pair关系，都错误，即(10,1)、(10,2)、(10,3)、(10,4)、(10,5)，故方法2的auc为(25-4-5)/25=0.64，因而正如直观所见，分类方法1要优于分类方法2。

回归问题的条件/前提：

1）收集的数据

2）假设的模型，即一个函数，这个函数里含有未知的参数，通过学习，可以估计出参数。然后利用这个模型去预测/分类新的数据。

# coding: utf-8

'''

Created on Oct 27, 2010

Logistic Regression Working Module

@author: Peter

'''

from numpy import *

def loadDataSet():

    dataMat = []; labelMat = []

    fr = open('testSet.txt')

    for line in fr.readlines():

        lineArr = line.strip().split()

        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # three feature

        labelMat.append(int(lineArr[2]))

    return dataMat,labelMat

def sigmoid(inX):

    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):

    dataMatrix = mat(dataMatIn)             #convert to NumPy matrix

    labelMat = mat(classLabels).transpose() #convert to NumPy matrix  # 行向量转化为列向量，转置

    m,n = shape(dataMatrix)

    alpha = 0.001

    maxCycles = 500

    weights = ones((n,1))

    for k in range(maxCycles):              #heavy on matrix operations

        h = sigmoid(dataMatrix*weights)     #matrix mult

        error = (labelMat - h)              #vector subtraction

        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult  ##中间过程略：∂J(w)/∂w=1/2∂w(∑(hw(x)−y)2)=(hw(x)−y)x(i)

    return weights

def stocGradAscent0(dataMatrix, classLabels):

    m,n = shape(dataMatrix)

    alpha = 0.01

    weights = ones(n)   #initialize to all ones

    for i in range(m):

        h = sigmoid(sum(dataMatrix[i]*weights))

        error = classLabels[i] - h

        weights = weights + alpha * error * dataMatrix[i]

    return weights

def stocGradAscent1(dataMatrix, classLabels, numIter=150): #

    m,n = shape(dataMatrix)

    weights = ones(n)   #initialize to all ones

    for j in range(numIter):

        dataIndex = range(m)

        for i in range(m):

            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not    # 学习率越来越低

            randIndex = int(random.uniform(0,len(dataIndex))) # go to 0 because of the constant

            h = sigmoid(sum(dataMatrix[randIndex]*weights))  # 随机选择样本

            error = classLabels[randIndex] - h

            weights = weights + alpha * error * dataMatrix[randIndex]

            del(dataIndex[randIndex])

    return weights

def classifyVector(inX, weights):

    prob = sigmoid(sum(inX*weights))

    if prob > 0.5: return 1.0

    else: return 0.0

1. 线性回归

假设特征和结果都满足线性。即不大于一次方。这个是针对收集的数据而言。
收集的数据中，每一个分量，就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数，向量表示形式：

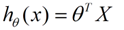
这个就是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。一个线性矩阵方程，直接求解，很可能无法直接求解。有唯一解的数据集，微乎其微。

基本上都是解不存在的超定方程组。因此，需要退一步，将参数求解问题，转化为求最小误差问题，求出一个最接近的解，这就是一个松弛求解。

求一个最接近解，直观上，就能想到，误差最小的表达形式。仍然是一个含未知参数的线性模型，一堆观测数据，其模型与数据的误差最小的形式，模型与数据差的平方和最小：

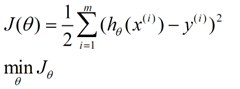
这就是损失函数的来源。接下来，就是求解这个函数的方法，有最小二乘法，梯度下降法。

最小二乘法

是一个直接的数学求解公式，不过它要求X是列满秩的，

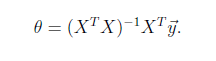
梯度下降法

分别有梯度下降法，批梯度下降法，增量梯度下降。本质上，都是偏导数，步长/最佳学习率，更新，收敛的问题。这个算法只是最优化原理中的一个普通的方法，可以结合最优化原理来学，就容易理解了。

2. 逻辑回归

逻辑回归与线性回归的联系、异同？

逻辑回归的模型是一个非线性模型，sigmoid函数，又称逻辑回归函数。但是它本质上又是一个线性回归模型，因为除去sigmoid映射函数关系，其他的步骤，算法都是线性回归的。可以说，逻辑回归，都是以线性回归为理论支持的。

只不过，线性模型，无法做到sigmoid的非线性形式，sigmoid可以轻松处理0/1分类问题。

另外它的推导含义：仍然与线性回归的最大似然估计推导相同，最大似然函数连续积（这里的分布，可以使伯努利分布，或泊松分布等其他分布形式），求导，得损失函数。

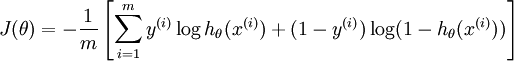
逻辑回归函数

表现了0,1分类的形式。

应用举例：

是否垃圾邮件分类？

是否肿瘤、癌症诊断？

是否金融欺诈？

3. 一般线性回归：

http://deeplearning.stanford.edu/wiki/index.php/Softmax_Regression

线性回归是以高斯分布为误差分析模型；逻辑回归采用的是伯努利分布分析误差。而高斯分布、伯努利分布、贝塔分布、迪特里特分布，都属于指数分布。

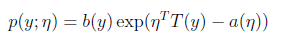
而一般线性回归，在x条件下，y的概率分布 p(y|x) 就是指指数分布. 经历最大似然估计的推导，就能导出一般线性回归的误差分析模型（最小化误差模型）。

softmax回归就是一般线性回归的一个例子。

有监督学习回归，针对多类问题（逻辑回归，解决的是二类划分问题），如数字字符的分类问题，0-9,10个数字，y值有10个可能性。

而这种可能的分布，是一种指数分布。而且所有可能的和为1，则对于一个输入的结果，其结果可表示为：

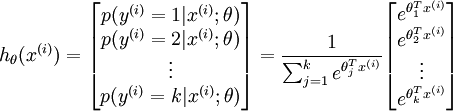参数是一个k维的向量。

而代价函数：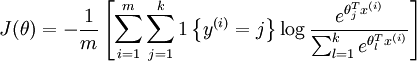

是逻辑回归代价函数的推广。而对于softmax的求解，没有闭式解法（高阶多项方程组求解），仍用梯度下降法，或L-BFGS求解。当k=2时，softmax退化为逻辑回归，这也能反映softmax回归是逻辑回归的推广。

4. 拟合：拟合模型/函数

由测量的数据，估计一个假定的模型/函数。如何拟合，拟合的模型是否合适？可分为以下三类

合适拟合

欠拟合

过拟合

过拟合的问题如何解决？

问题起源？模型太复杂，参数过多，特征数目过多。

方法： 1）减少特征的数量，有人工选择，或者采用模型选择算法：http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html （特征选择算法的综述）

2）正则化，即保留所有特征，但降低参数的值的影响。正则化的优点是，特征很多时，每个特征都会有一个合适的影响因子。

5. 概率解释：线性回归中为什么选用平方和作为误差函数？

假设模型结果与测量值误差满足，均值为0的高斯分布，即正态分布。这个假设是靠谱的，符合一般客观统计规律。

数据x与y的条件概率：

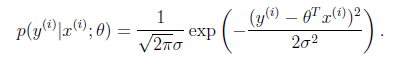
若使模型与测量数据最接近，那么其概率积就最大。概率积，就是概率密度函数的连续积，这样，就形成了一个最大似然函数估计。对最大似然函数估计进行推导，就得出了求导后结果：平方和最小公式

7. 错误函数/代价函数/损失函数：

线性回归中采用平方和的形式，一般都是由模型条件概率的最大似然函数概率积最大值，求导，推导出来的。

统计学中，损失函数一般有以下几种：

1） 0-1损失函数

L(Y,f(X))={1,0,Y≠f(X)Y=f(X)

2）平方损失函数

L(Y,f(X))=(Y−f(X))2

3）绝对损失函数

L(Y,f(X))=|Y−f(X)|

4）对数损失函数

L(Y,P(Y|X))=−logP(Y|X)

损失函数越小，模型就越好，而且损失函数尽量是一个凸函数，便于收敛计算。

线性回归，采用的是平方损失函数。而逻辑回归采用的是对数损失函数。这些仅仅是一些结果，没有推导。

正则化：

为防止过度拟合的模型出现（过于复杂的模型），在损失函数里增加一个每个特征的惩罚因子。这个就是正则化。如正则化的线性回归的损失函数：

lambda就是惩罚因子。

正则化是模型处理的典型方法。也是结构风险最小的策略。在经验风险（误差平方和）的基础上，增加一个惩罚项/正则化项。线性回归的解，也从θ=(XTX)−1XTy

转化为

括号内的矩阵，即使在样本数小于特征数的情况下，也是可逆的。逻辑回归的正则化：

从贝叶斯估计来看，正则化项对应模型的先验概率，复杂模型有较大先验概率，简单模型具有较小先验概率。这个里面又有几个概念。什么是结构风险最小化？先验概率？模型简单与否与先验概率的关系？

经验风险、期望风险、经验损失、结构风险

期望风险（真实风险），可理解为模型函数固定时，数据平均的损失程度，或“平均”犯错误的程度。期望风险是依赖损失函数和概率分布的。只有样本，是无法计算期望风险的。

所以，采用经验风险，对期望风险进行估计，并设计学习算法，使其最小化。即经验风险最小化（Empirical Risk Minimization）ERM，而经验风险是用损失函数来评估的、计算的。对于分类问题，经验风险，就训练样本错误率。对于函数逼近，拟合问题，经验风险，就平方训练误差。对于概率密度估计问题，ERM，就是最大似然估计法。

而经验风险最小，并不一定就是期望风险最小，无理论依据。只有样本无限大时，经验风险就逼近了期望风险。如何解决这个问题？统计学习理论SLT，支持向量机SVM就是专门解决这个问题的。有限样本条件下，学习出一个较好的模型。由于有限样本下，经验风险Remp[f]无法近似期望风险R[f] 。因此，统计学习理论给出了二者之间的关系：R[f] <= ( Remp[f] + e )

而右端的表达形式就是结构风险，是期望风险的上界。而e = g(h/n)是置信区间，是VC维h的增函数，也是样本数n的减函数。VC维的定义在 SVM，SLT中有详细介绍。e依赖h和n，若使期望风险最小，只需关心其上界最小，即e最小化。所以，需要选择合适的h和n。这就是结构风险最小化Structure Risk Minimization，SRM. SVM就是SRM的近似实现，SVM中的概念另有一大筐。就此打住。

1范数，2范数的物理意义：

范数，能将一个事物，映射到非负实数，且满足非负性，齐次性，三角不等式。是一个具有“长度”概念的函数。

1范数为什么能得到稀疏解？

压缩感知理论，求解与重构，求解一个L1范数正则化的最小二乘问题。其解正是欠定线性系统的解。

2范数为什么能得到最大间隔解？

2范数代表能量的度量单位，用来重构误差。

以上几个概念理解需要补充。

牛顿法求解最大似然估计

前提条件：求导迭代，似然函数可导，且二阶可导。

迭代公式：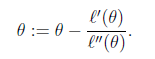

若是向量形式，

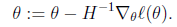
H就是 n*n 的hessian矩阵了。

特征：当靠近极值点时，牛顿法能快速收敛，而在远离极值点的地方，牛顿法可能不收敛。这个的推导？

这点是与梯度下降法的收敛特征是相反的。

核函数的物理意义：

映射到高维，使其变得线性可分。什么是高维？如一个一维数据特征x，转换为（x，x^2, x^3），就成为了一个三维特征，且线性无关。一个一维特征线性不可分的特征，在高维，就可能线性可分了。

Regression问题的常规步骤为：

寻找h函数（即hypothesis）；
构造J函数（损失函数）；
想办法使得J函数最小并求得回归参数（θ）

构造预测函数h

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

Sigmoid 函数在有个很漂亮的“S”形，如下图所示（引自维基百科）：

下面左图是一个线性的决策边界，右图是非线性的决策边界。

对于线性边界的情况，边界形式如下：

构造预测函数为：

函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

构造损失函数J

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

下面详细说明推导的过程：

（1）式综合起来可以写成：

取似然函数为：

对数似然函数为：

最大似然估计就是求使取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。但是，在Andrew Ng的课程中将取为下式，即：

因为乘了一个负的系数-1/m，所以取最小值时的θ为要求的最佳参数。

梯度下降法求的最小值

θ更新过程：

θ更新过程可以写成：

向量化Vectorization

Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。

如上式，Σ(...)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。

下面介绍向量化的过程：

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知可由一次计算求得。

θ更新过程可以改为：

综上所述，Vectorization后θ更新的步骤如下：

（1）求；

（2）求；

（3）求。

Reference：

逻辑回归