k3 cloud中列表字段汇总类型中设置了汇总以后没有显示出汇总值

处理方法,需要bos中的分组列信息中设置求和:
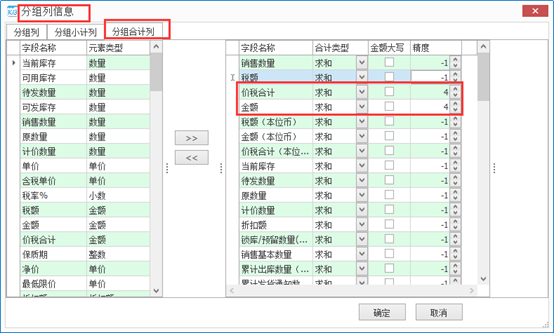
选择对应字段将其从左侧添加到右侧
方法二:
直接针对【价税合计】字段的列表汇总类型进行设置,步骤如下图所示
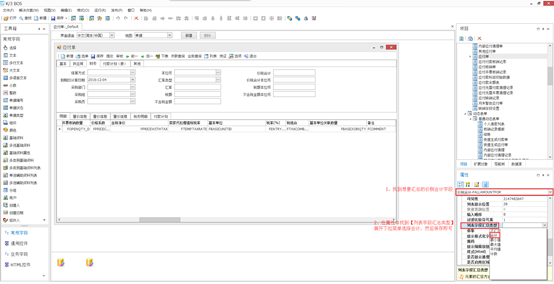
k3 cloud中列表字段汇总类型中设置了汇总以后没有显示出汇总值的更多相关文章
- 当数据库中的字段与javabean中对应的属性名不同
当数据库中的字段与javabean中对应的属性名不同时: 在查询语句中对不同的字段起别名,例如: 数据库中的字段名为last_name , javabean中为lastName则:select las ...
- mybitis中对象字段与表中字段名称不匹配(复制)
开发中,实体类中的属性名和对应的表中的字段名不一定都是完全相同的,这样可能会导致用实体类接收返回的结果时导致查询到的结果无法映射到实体类的属性中,那么该如何解决这种字段名和实体类属性名不相同的冲突呢? ...
- 为什么HTML中的多个空格或是回车在浏览器上只能显示出一个?
我们在学习HTML的时候可能书本或是老师会告诉我们一件事,就是在HTML中不管我们在两个文本之间加上多少连续的空格或是回车,到了浏览器里面只能显示出一个来.但是我们从来不知道为什么. 原因很简单,因为 ...
- k3 cloud移动审批提示实体类型BD_TaxRate中不存在名为AmountDigits属性
原因是由于字段没有正确绑定币别,找到对应的字段并修改绑定币别
- mysql中修改字段的类型
修改表字段的类型: ALTER TABLE 表名 MODIFY COLUMN 字段名 字段类型定义 如:将movie_mark修改为浮点型 alter table new_playing_video ...
- 用grep在子目录中指定的文件类型中查找(转载)
转自:http://www.ai7.org/wp/html/653.html grep -r abcd *.py 这样的命令得不到你期待的结果,而 grep -r abcd * 这样得到的结果又太多, ...
- 将List中部分字段转换为DataTable中
由于原来方法导出数据量比较大 的时候,出现卡顿现象:搜索简单改造:(下面方法借助NPIO) /// <summary> /// 将List中原文和译文转换为Datatable /// &l ...
- 设置UIButton中的文字和图片,设置UILabel的文在显示不同颜色
UIButton: UIEdgeInsets 在UIButton中有三个对EdgeInsets的设置:ContentEdgeInsets.titleEdgeInsets.imageEdgeInsets ...
- Elasticsearch入门必备——ES中的字段类型以及常用属性
使用Elasticsearch时,了解字段的概念,是必不可少的.毕竟无论是es还是传统的数据库,都无法弱化字段的类型. 背景知识 在Es中,字段的类型很关键: 在索引的时候,如果字段第一次出现,会自动 ...
随机推荐
- Git命令——撤销修改
Git命令 1. 撤销修改 (1) 当改乱了工作区(working directory)某个文件的内容,想直接丢弃工作区中的修改时,用命令git checkout -- file. (2) 当不但改乱 ...
- java 生成时机时间
import java.text.SimpleDateFormat; import java.util.Date; import java.util.Random; public class t ...
- CF1009F Dominant Indices 长链剖分
题目传送门 https://codeforces.com/contest/1009/problem/F 题解 长链剖分的板子吧. 令 \(dp[x][i]\) 表示 \(x\) 的子树中的深度为 \( ...
- Vue的自定义滚动,我用el-scrollbar
弄了一个持续更新的github笔记,可以去看看,诚意之作(本来就是写给自己看的--)链接地址:Front-End-Basics 此篇文章的地址:Vue的自定义滚动,我用el-scrollbar 基础笔 ...
- django之创建项目
1.创建虚拟环境 mkvirtualenv django_study -p python3 创建成功后:(django_study) python@ubuntu:~$ 2.安装django-指定版本1 ...
- 6.dockerfile
一.概述 自制镜像的目的不是为了解决配置更新的问题,而是为了定制化应用服务. 镜像的制作:基于容器制作:dockerfile dockerfile的格式:注释信息+指令(约定俗成使用大写)及其参数 d ...
- Linux下安装Python,以及环境变量的配置
1.安装环境 centos7 + vmware + xshell 2.安装Python3 2.1下载Python资源包 网址:https://www.python.org/downloads/re ...
- bootstrap 的布局
第一步:你要做的就是选择适合你显示器的标签: .col-xs- 超小屏幕 手机 (<768px) .col-sm- 小屏幕 平板 (≥768px) .col-md- 中等屏幕 桌面显示器 (≥9 ...
- SQL语句中 (+) 含义
(+) 表示外连接.条件关联时,一般只列出表中满足连接条件的数据.如果条件的一边出现(+),则可列出该表中在条件另一侧的数据为空的那些记录.比如两个表:员工表和工资表.员工表中有总经理.A.B.C四条 ...
- Winner
Winner 南昌邀请赛 暴力模拟 #include<bits/stdc++.h> using namespace std; struct Nod { int i; int a,b,c; ...
