[CSP-S模拟测试]:你相信引力吗（单调栈）

题目传送门（内部题124）

---

输入格式

　　第一行一个整数$n$代表环的长度。
　　第二行$n$个整数表示每个冰锥的高度。

---

输出格式

　　一行一个整数表示有多少对冰锥是危险的。

---

样例

样例输入1：

5
1 2 4 5 3

样例输出1：

7

样例输入2：

3
7 7 7

样例输出2：

3

---

数据范围与提示

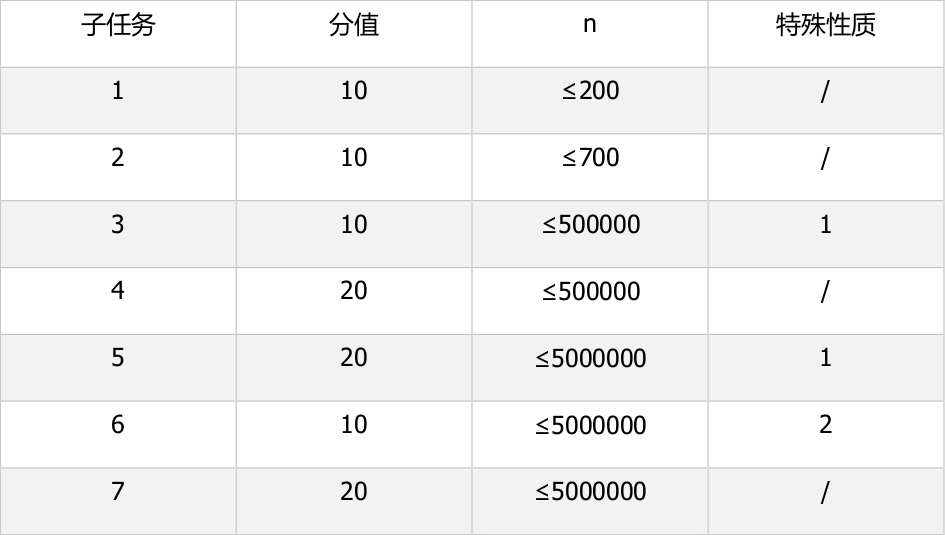
对于所有数据，满足$3\leqslant n\leqslant 5,000,000$，$0\leqslant$冰锥的高度$\leqslant 10^9$。
特殊性质$1$：高度是一个单调不降的序列
特殊性质$2$：不包含两个高度相同的冰锥
本题读入量较大，建议使用较快速的读入方式

---

题解

先来解释一下题意，应该是$i$或$j$的高度，而不是$i$和$j$的高度，样例$1$即为下图$\downarrow$

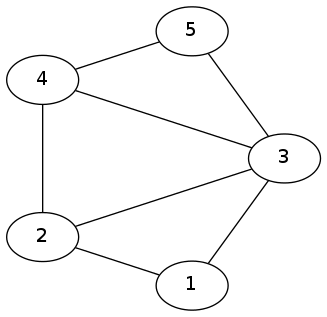
首先，有这么一个性质，对于一个冰锥，它对答案的贡献为它相邻的冰锥开始的一个不降序列的长度且不大于这个点的高度。

那么可以用单调栈维护。

再来处理第一个难点，环。

对于环的问题，直接将其复制一遍，而对于这道题，为了方便，直接从序列中最大的一个开始即可。

第二个难点，重复。

也不用担心，再开一个数组记录一下当前栈中每一个元素跟前面的元素有几个相同即可。

注意数据范围冰锥的高度其实是$2\times 10^9$即可。

这道题卡常，所以要使用$AE86$。

时间复杂度：$\Theta(n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n;
int a[10000001],sta[10000001],sam[10000001],mx,top;
namespace ae86{
	const int bufl=1<<15;
	char buf[bufl],*s=buf,*t=buf;
	inline int fetch(){
		if(s==t){t=(s=buf)+fread(buf,1,bufl,stdin);if(s==t)return EOF;}
		return*s++;
	}
	inline int read(){
	int a=0,b=1,c=fetch();
		while(!isdigit(c))b^=c=='-',c=fetch();
		while(isdigit(c))a=a*10+c-48,c=fetch();
		return b?a:-a;
	}
}
using ae86::read;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		a[i+n]=a[i]=read();
		if(a[i]>a[mx])mx=i;
	}
	long long ans=0;
	for(int i=mx;i<mx+n;i++)
	{
		while(top&&sta[top]<a[i]){ans++;top--;}
		if(sta[top]>a[i])ans++;
		else ans+=sam[top]+(a[i]!=a[mx]);
		sta[++top]=a[i];
		sam[top]=(a[i]==sta[top-1]?sam[top-1]+1:1);
	}
	while(top>2)
	{
		if(sta[top]==sta[2])break;
		top--;ans++;
	}
	printf("%lld",ans);
	return 0;
}

---

rp++