zay大爷的膜你题 D2T2——不老梦（AK梦）

还是万年不变的外链

这个题。。。。。是最难的。。。。但是不知道为啥扶苏神仙讲完了之后我竟然听懂了。。。。

所以这个题我要好好写一写

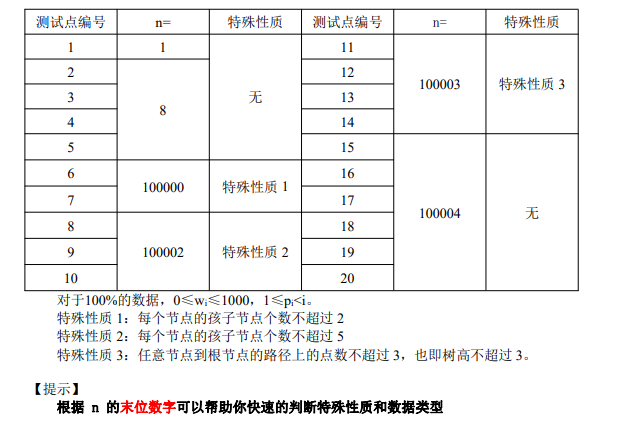
首先我们看一看每一个测试点，来一点点得分

第一个测试点n = 1，直接输出w1就行，5分到手

第2-5个点，数据范围很小，我们可以打深搜

因为n = 8，所以即使是全排列也无非是8！，小的可怜，然后o（n）地check一遍是不是合法，所以最后的时间复杂度是O（n！n）

要考虑排列顺序一定是保证某个点的所有儿子都出现之后才能出现，否则不合法，而对于合法的排列，我们计算其w值，并且min（ans，w的和），最后输出ans即可，然后就又拿到了20分

第6-7个点，我们可以发现那玩意是个二叉树，这个就好办多了，

我们考虑这样一个东西

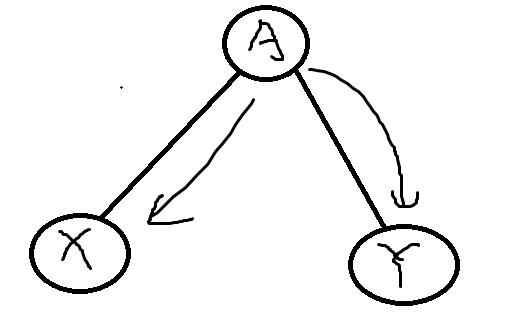
现在我们扫到了一个根节点为a的点，他有两个儿子分别是x，y，如果先进入x，那么我们需要的石子数就是W[x](指的是其子树的和)+w[a]，同理，先进去y的话，我们需要的石子数就是W[y](指的是其子树的和)+w[a]，假设w[y]更大的话，我们先进入y，当我们把y的子树放满了，我们就可以放y这个点了，在把y放上之后，我们可以把y的所有子树的石子拿出来扔到x的子树里去，这样不仅能不多用石子，甚至还有可能多余出石子放在a里，要是你先进x的话，就会导致你还得多带上w[y] - w[x]个石子，否则你将放不满y的子树，这样就不合法了

因为是二叉树，所以直接判断就好啦,最后所有答案加起来就是结果啦

测试点8-10,因为最多只有5个孩子，又因为n不算太大，我们可以暴力算出选孩子的顺序看那个最优秀，时间复杂度是O(5! n),说实话5！ = 120的话，最后也不过是1e6多一点，正常跑就行了

测试点 11-14： 树高最多为 3。考虑进入第 3 层时由于不能回收石子，所以进入第三层的顺序无所谓，即对于第 2 层的每个节点 u,都有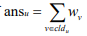。现在只需要考虑从 1 号节点 进入它的所有孩子节点的顺序即可。 考虑走完节点 u 的所有孩子 v 所需要的总石子数 c[u]，显然是越少越好。证明如 下： 走完所有孩子后，所花费的总石子数不变，设剩下的石子(也就是所需要的减去所 花费的)为 ret，注意到当 c[u] 最小的时候即是 ret 最小的时候。考虑当 ret ≥ wu 的时候，直接用 ret 放下 u 上的石子，于是放石子在节点 u 的总花费就是 c[u]，后者 越小越好。 当 ret < w[u] 的时候，用剩下的石子放在 u 上，然后再额外放上去一些石子，这 样做的花费是 ，这显然是最小的花费，考虑当 c[u] 越小 ret 才越小，c[u]取 最小时显然能取到最优情况。 综上，可以尽可能使 c[u]减小，来达到最优解。 那么问题变成了： 有 x 个商品，购买第 i 个物品需要手里有 ansi 元钱，花费 wi 元。求一个顺序 使得购买所有商品所需要的钱数最少。 这个问题的最最优顺序是按照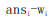不升序购买，也就是差值越大越要先买。 考虑证明： 设有两个物品 i,j，设 ai=ansi-wi，aj=ansj-wj。且 ai>aj。考虑先买 i 再买 j 的 花费是 max(ansi, wi+ansj) ①，同理先买 j 的花费是 max(ansj, wj+ansi) ②。 提出 w，则 ①=wi+max(ai,ansj)，②=wj+max(aj,ansi)=wj+max(aj,ai+wi)=wj+ai+wi。 考虑 ① 式的 max 如果取前面一项，则 ①=wi+ai<②，如果取后面一项则 ① =wi+ansj=wi+aj+wj<②，于是无论怎么取，①式恒小于②式，于是先买 i 更优。数学归纳法可得按照 ansi-wi 不升序购买最优。

最后贴一下代码吧

#include <cstdio>
#include <vector>
#include <algorithm>

const int maxn = ;

int n;
int MU[maxn], ans[maxn];
std::vector<int>son[maxn];

void dfs(const int u);
bool cmp(const int &_a, const int &_b);

int main() {
  freopen("yin.in", "r", stdin);
  freopen("yin.out", "w", stdout);
  scanf("%d", &n);
  for (int i = , x; i <= n; ++i) {
    scanf("%d", &x);
    son[x].push_back(i);
  }
  for (int i = ; i <= n; ++i) {
    scanf("%d", MU + i);
  }
  dfs();
  for (int i = ; i < n; ++i) {
    printf("%d ", ans[i]);
  }
  printf("%d\n", ans[n]);
  return ;
}

void dfs(const int u) {
  for (auto v : son[u]) {
    dfs(v);
  }
  std::sort(son[u].begin(), son[u].end(), cmp);
  int _ret = ;
  for (auto v : son[u]) {
    if (_ret >= ans[v]) {
      _ret -= ans[v];
    } else {
      ans[u] += ans[v] - _ret;
      _ret = ans[v] - MU[v];
    }
  }
  ans[u] += std::max(, MU[u] - _ret);
}

inline bool cmp(const int &_a, const int &_b) {
  return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]);
}

还有。。。。。。。c++11是个好东西可惜我不会。。。。。。。。