POJ - 3176 Cow Bowling 动态规划

动态规划：多阶段决策问题，每步求解的问题是后面阶段问题求解的子问题，每步决策将依赖于以前步骤的决策结果。（可以用于组合优化问题）

优化原则：一个最优决策序列的任何子序列本身一定是相当于子序列初始和结束状态的最优决策序列。

只有满足优化原则的问题才可以利用动态算法进行求解，因为只有全局最优解法等于其每个子问题的最优才可以分阶段进行求解。

The cows don't use actual bowling balls when they go bowling. They each take a number (in the range 0..99), though, and line up in a standard bowling-pin-like triangle like this:

          7

        3   8

      8   1   0

    2   7   4   4

  4   5   2   6   5

Then the other cows traverse the triangle starting from its tip and moving "down" to one of the two diagonally adjacent cows until the "bottom" row is reached. The cow's score is the sum of the numbers of the cows visited along the way. The cow with the highest score wins that frame.

Given a triangle with N (1 <= N <= 350) rows, determine the highest possible sum achievable.

Input

Line 1: A single integer, N

Lines 2..N+1: Line i+1 contains i space-separated integers that represent row i of the triangle.

Output

Line 1: The largest sum achievable using the traversal rules

Sample Input

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Sample Output

30

Hint

Explanation of the sample:

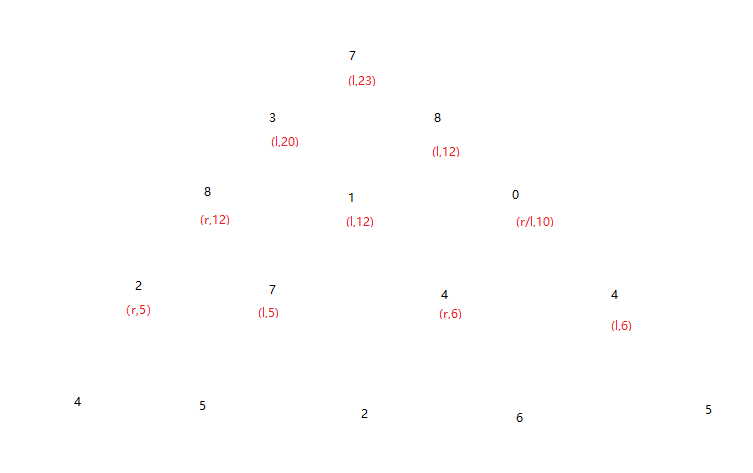
          7

         *

        3   8

       *

      8   1   0

       *

    2   7   4   4

       *

  4   5   2   6   5

The highest score is achievable by traversing the cows as shown above.

这道题的思路解法是：记录n-1层的每个元素值到n层的最大距离，再计算n-2层到n层=n-2到n-1+n-1到n，然后n-3到n=n-3到n-2+n-2到n;一直如此循环直到第一层

 

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=355;
int main()
{
int sum=0,a[maxn][maxn],b[maxn][maxn],c[maxn][maxn]; //a记录每个位置牛的编号 ，b[i][j]记录从(i,j)位置往下走的最大编号和但不包括a[i][j]本身
int n;
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
scanf("%d",&a[i][j]); //存储每头牛的编号
for(int i=n-1;i>=1;i--)
{
for(int j=1;j<=i;j++)
{
if(a[i+1][j]+b[i+1][j]>=a[i+1][j+1]+b[i+1][j+1]) b[i][j]=b[i+1][j]+a[i+1][j],c[i][j]=0; //c记录走的路径
else b[i][j]=b[i+1][j+1]+a[i+1][j+1],c[i][j]=1;
}
}
/*cout<<a[1][1]<<endl; //注释掉的内容所走的路径
for(int i=1,j=1;i<n;i++)
{
cout<<a[i+1][j+c[i][j]]<<endl;
j=j+c[i][j];

}*/
cout<<a[1][1]+b[1][1]<<endl;
return 0;
}