【XSY2760】nonintersect 计算几何

题目描述

　　平面上有\(n\)条线段，你要擦掉所有线段但保留原有的\(2n\)个端点，然后连接这些端点形成\(n\)条不相交的线段，每个端点只能在一条线段中。

　　假设你画的线段总长为\(Y\)，原有线段的总长为\(X\)，你要满足\(Y\geq \frac{2}{\pi}X\)

　　\(n\leq 5000\)

题解

　　我们先随便画一个向量，把所有向量投影到这个向量上面。

　　若一个确定的向量\(\overrightarrow a\)的倾角为\(x\)，另一个随机的单位向量\(\overrightarrow b\)的倾角为\(\theta\)，那么\(\overrightarrow a\)在\(\overrightarrow b\)上的投影的长度为\(|a||\cos (x-\theta)|\)。这个东西的期望为\(|a|\frac{2}{\pi}\)。

　　所以随机一个向量，所有向量在这个向量的投影上的长度之和\(>\frac{2}{\pi}X\)的概率为\(\frac{1}{2}\)。

　　你可以多随机几次，也可以用一个确定性的算法算出上面这个东西。

　　怎么算？

　　假设后面那部分没有绝对值符号。把\(|a|\cos(x-\theta)\)展开成$|a|\sin x\sin \theta+|a|\cos x\cos \theta \(，把这些东西加起来得到\)c\sin \theta + d\cos \theta\(。现在我们要求这个东西的最大值。\)(c\sin \theta + d\cos \theta)'=c\cos \theta - d \sin \theta\(，那么\)\frac{c}{d}=\tan \theta$，然后就可以算出投影的长度。

　　但是现在有绝对值符号。

　　先把所有向量翻到\(x\)轴上方，按极角排序。

　　

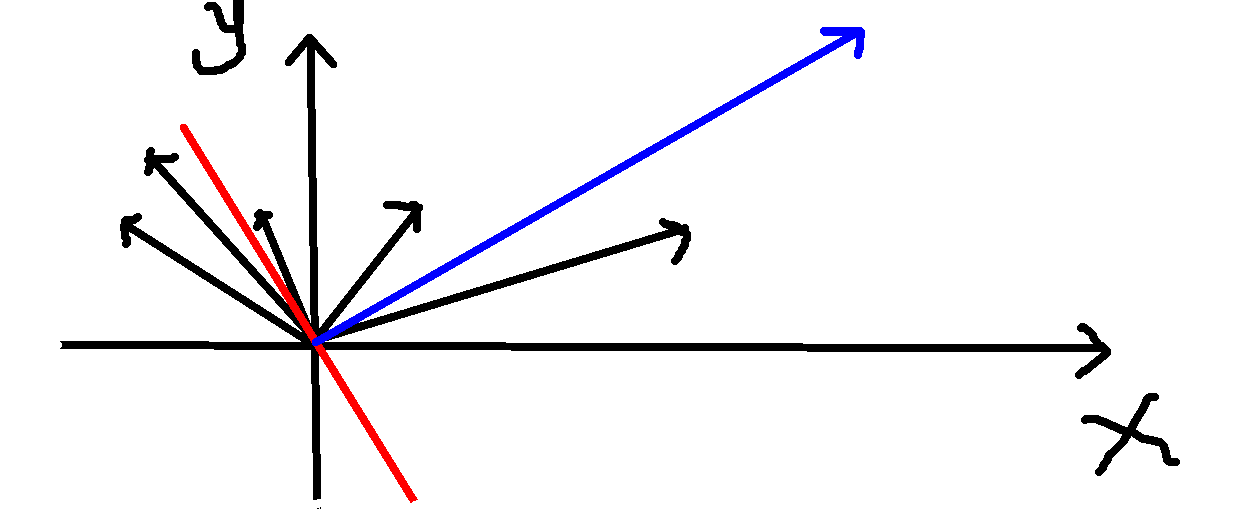
　　假设最优的是蓝色这个向量。

　　我们枚举和这个向量垂直的直线（红色），那么直线左边的向量\(\cos(x-\theta)\)的符号就是负的，右边的就是正的。

　　所以我们可以在\(O(n\log n)\)内把最优的向量算出来。

　　接下来把所有\(2n\)点投影在这个向量上，取左边一半的点作为我们要连的线段的左端点，右边一半的点作为右端点。这样连出来的长度肯定比原有的线段在这个向量上投影的长度大。

　　这样我们就得到了两个分离的点集，现在要在这两个点集间连线。

　　有两种方法：

　　第一种：取左下方的点集最左下的点，然后枚举右侧点集中的一个点，要求这两个点连成的直线下方的点中每个点集的点各占一半。把这两个点连起来，然后分治成小问题。

　　时间复杂度：期望\(O(n\log^2n)\)，最坏\(O(n^2\log n)\)

　　第二种：求这两个点集合并后的凸包，删掉凸包上相邻两个属于不同的点集的点，把这两个点连起来，重复前面的过程。

　　时间复杂度：\(O(n^2)\)

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<utility>
#include<vector>
using namespace std;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
typedef long long ll;
const double pi=acos(-1);
const double eps=1e-9;
struct point
{
	double x,y;
	point(){}
	point(const double &a,const double &b):x(a),y(b){}
};
point operator +(point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator -(point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator *(point a,double b){return point(a.x*b,a.y*b);}
int operator <(point a,point b){if(a.x!=b.x)return a.x<b.x;return a.y<b.y;}
double dot(point a,point b){return a.x*b.x+a.y*b.y;}
double cross(point a,point b){return a.x*b.y-a.y*b.x;}
double len(point a){return sqrt(a.x*a.x+a.y*a.y);}
struct point2
{
	int x,y;
	point2(int a=0,int b=0)
	{
		x=a;
		y=b;
	}
};
point2 operator +(const point2 &a,const point2 &b){return point2(a.x+b.x,a.y+b.y);}
point2 operator -(const point2 &a,const point2 &b){return point2(a.x-b.x,a.y-b.y);}
point2 operator *(const point2 &a,const int &b){return point2(a.x*b,a.y*b);}
int operator <(const point2 &a,const point2 &b){if(a.x!=b.x)return a.x<b.x;return a.y<b.y;}
ll dot(const point2 &a,const point2 b){return (ll)a.x*b.x+(ll)a.y*b.y;}
ll cross(const point2 &a,const point2 &b){return (ll)a.x*b.y-(ll)a.y*b.x;}
double len(point2 a){return sqrt((double)a.x*a.x+(double)a.y*a.y);}
struct ppp
{
	point2 x;
	int y;
	double v;
	pdd a;
};
ppp c[10010];
point2 a[10010];
pii d[5010];
int cmp(ppp a,ppp b)
{
	return a.v<b.v;
}
int n;
int link[10010];
int v1[10010],v2[10010];
int t1,t2;
int cmp2(int x,int y)
{
	if(a[x].x!=a[y].x)
		return a[x].x<a[y].x;;
	return a[x].y<a[y].y;
}
int color[10010];
int b[10010];
int st[10010];
int top;
pdd operator +(pdd a,pdd b){return pdd(a.first+b.first,a.second+b.second);}
pdd operator -(pdd a,pdd b){return pdd(a.first-b.first,a.second-b.second);}
pdd f1[10010];
pdd f2[10010];
struct pppp
{
	point x;
	int y;
};
pppp e[10010];
int cmp3(pppp a,pppp b)
{
	return a.x<b.x;
}
int main()
{
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
#endif
	scanf("%d",&n);
	for(int i=1;i<=2*n;i++)
		scanf("%d%d",&a[i].x,&a[i].y);
	int x,y;
	double s=0,ans;
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&d[i].first,&d[i].second);
		s+=len(a[d[i].first]-a[d[i].second]);
		c[i].x=a[d[i].second]-a[d[i].first];
		if(c[i].x.y<0)
		{
			c[i].x.x=-c[i].x.x;
			c[i].x.y=-c[i].x.y;
		}
		c[i].y=i;
		c[i].v=atan2(c[i].x.y,c[i].x.x);
		c[i].a.first=len(c[i].x)*sin(c[i].v);
		c[i].a.second=len(c[i].x)*cos(c[i].v);
	}
	sort(c+1,c+n+1,cmp);
	for(int i=1;i<=n;i++)
		f1[i]=f1[i-1]+c[i].a;
	double mx=0,angle;
	for(int i=0;i<=n;i++)
	{
		double now_angle=atan2(f1[n].first-2*f1[i].first,f1[n].second-2*f1[i].second);
		if(now_angle<0)
			now_angle+=2*pi;
		double now=(f1[n].first-2*f1[i].first)*sin(now_angle)+(f1[n].second-2*f1[i].second)*cos(now_angle);
		if(now>mx)
		{
			mx=now;
			angle=now_angle;
		}
	}
	point r(cos(angle),sin(angle));
	for(int i=1;i<=2*n;i++)
	{
		e[i].x=r*dot(point(a[i].x,a[i].y),r);
		e[i].y=i;
	}
	sort(e+1,e+2*n+1,cmp3);
	for(int i=1;i<=n;i++)
		color[e[i].y]=1;
	for(int i=n+1;i<=2*n;i++)
		color[e[i].y]=2;
	t1=t2=0;
	for(int i=1;i<=2*n;i++)
		v1[++t1]=i;
	sort(v1+1,v1+t1+1,cmp2);
	for(int i=1;i<=n;i++)
	{
		top=0;
		t2=t1;
		for(int i=1;i<=t1;i++)
			v2[i]=v1[i];
		for(int j=1;j<=t1;j++)
		{
			x=v1[j];
			while(top>=2&&cross(a[x]-a[st[top-1]],a[st[top]]-a[st[top-1]])>0)
				top--;
			st[++top]=x;
		}
		int flag=1;
		for(int i=1;i<top;i++)
			if(color[st[i]]!=color[st[i+1]])
			{
				link[st[i]]=st[i+1];
				link[st[i+1]]=st[i];
				b[st[i]]=b[st[i+1]]=1;
				flag=0;
				i++;
			}
		if(flag)
		{
			top=0;
			for(int j=t1;j>=1;j--)
			{
				x=v1[j];
				while(top>=2&&cross(a[x]-a[st[top-1]],a[st[top]]-a[st[top-1]])>0)
					top--;
				st[++top]=x;
			}
			for(int i=1;i<top;i++)
				if(color[st[i]]!=color[st[i+1]])
				{
					link[st[i]]=st[i+1];
					link[st[i+1]]=st[i];
					b[st[i]]=b[st[i+1]]=1;
					i++;
				}
		}
		t1=0;
		for(int i=1;i<=t2;i++)
			if(!b[v2[i]])
				v1[++t1]=v2[i];
	}
	for(int i=1;i<2*n;i++)
		if(link[i]>i)
			printf("%d %d\n",i,link[i]);
	return 0;
}