递归可视化之汉诺塔的动画实现(turtle海龟)
import turtle class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) ==
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - ]
def size(self):
return len(self.items) def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize()
t.speed()
t.goto(*(k-), )
t.down()
t.goto(*(k-), -)
t.goto(*(k-)-, -)
t.goto(*(k-)+, -)
drawpole_1()#画出汉诺塔的poles[]
drawpole_1()#画出汉诺塔的poles[]
drawpole_1()#画出汉诺塔的poles[] def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(,-i)
plates[i].goto(-,-+*i)
plates[i].showturtle()
return plates def pole_stack():#制造poles的栈
poles=[Stack() for i in range()]
return poles def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-)*,)
plates[mov].goto((tp-)*,)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-)*,-+*l) def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= :
moveTower(plates,poles,height-,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-,withPole,toPole,fromPole) myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[].push(i)
moveTower(plates,poles,n,,,)
myscreen.exitonclick()
运行结果(层数为5):
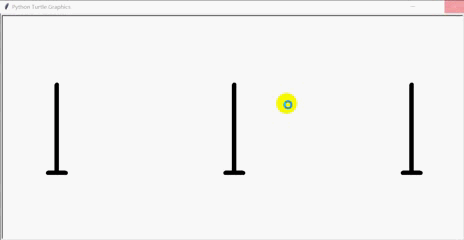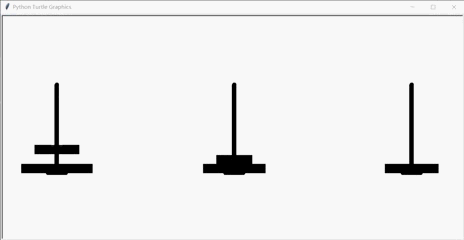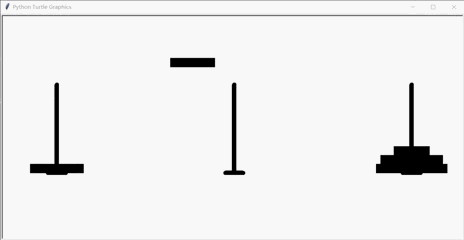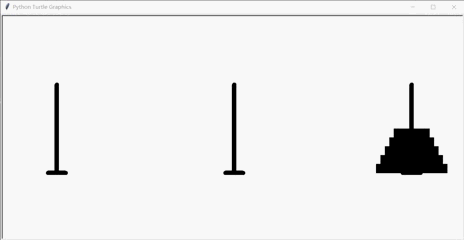
递归可视化之汉诺塔的动画实现(turtle海龟)的更多相关文章
- 递归--练习2--noi6261汉诺塔
递归--练习2--noi6261汉诺塔 一.心得 先把递推公式写出来,会很简单的 二.题目 6261:汉诺塔问题 总时间限制: 1000ms 内存限制: 65536kB 描述 约19世纪末,在欧州 ...
- py_递归实例:汉诺塔问题
递归的两个特点 调用自身 结束条件 # _*_coding:utf-8 ''' 递归实例:汉诺塔问题 n----盘子总数 a----第一个柱子 b----第二个柱子 c----第三个柱子 n个盘子时: ...
- 编程:递归编程解决汉诺塔问题(用java实现)
Answer: //Li Cuiyun,October 14,2016. //用递归方法编程解决汉诺塔问题 package tutorial_3_5; import java.util.*; publ ...
- 学C记录(理解递归问题之汉诺塔)
汉诺游戏规则如下: 1.有三根相邻的柱子,标号为A,B,C. 2.A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘. 3.现在把所有盘子一个一个移动到柱子B上,并且每次移动同一根柱子上都不能出现大盘 ...
- python中关于汉诺塔问题和使用turtle库实现其搬运过程
一.汉诺塔问题 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按 ...
- 关于C++的递归(以汉诺塔为例)
关于C++,hanoi塔的递归问题一直是个经典问题,我们学习数据结构的时候也会时常用到, 因为它的时间复杂度和空间复杂度都很高,我们在实际的应用中不推荐使用这种算法,移动n个盘子, 需要2的n次幂减一 ...
- C++入门经典-例4.3-函数的递归调用之汉诺塔问题
1:代码如下: // 4.3.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <iostream> using ...
- Python实现汉诺塔问题的可视化(以动画的形式展示移动过程)
学习Python已经有一段时间了,也学习了递归的方法,而能够实践该方法的当然就是汉诺塔问题了,但是这次我们不只是要完成对汉诺塔过程的计算,还要通过turtle库来体现汉诺塔中每一层移动的过程. 一.设 ...
- 运用Turtle实现汉诺塔的可视化运行(递归算法)
运用Turtle实现汉诺塔的可视化运行(递归算法) 汉诺塔问题又名河内塔问题,是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆 ...
随机推荐
- C# Directory.Exists() 文件存在但返回一直为false
备注:这是一个低级错误,起始真正的原因不是访问权限的问题. 真正的原因是:这个程序要读取远程电脑上共享文件夹里的文件,但是没有远程访问代码,导致找不到相关的目录.所以才报错! 查询一个文件,但程序突然 ...
- 前端使用crypto.js进行加密
前端使用crypto.js进行加密 https://www.cnblogs.com/lz2017/p/8046816.html 最近我在前端使用Cookies保存密码的时候需要前端来进行加密工作, ...
- SQL中的排名函数(ROW_NUMBER、RANK、DENSE_RANK、NTILE)简介
排名函数是Sql Server2005新增的功能,下面简单介绍一下他们各自的用法和区别. 在使用排名函数的时候需要注意以下三点: 1.排名函数必须有 OVER 子句. 2.排名函数必须有包含 ORDE ...
- C语言编程漫谈——main函数
写在前面 促使我写这篇文章是因为我这几天找了几个一样是大三的同学,与我相同专业相同方向(物联网)的人,除了@小胡同的诗,基本没有什么其他人会现在看起来很简单的编程题目了.问了一下其他同学,他们大部分都 ...
- 可编辑的div -> 编辑框
操作可编辑的div中,无可厚非,怎么获取当前光标位置,复制,粘贴等知识是必须要懂得,下边这个链接里面对其有详细的解释: 请点这里 想看详细的例子请点击这里
- C# xml 读xml、写xml、Xpath、Xml to Linq、xml添加节点 xml修改节点
#region XDocument //创建XDocument XDocument xdoc2 = new XDocument(); XElement xel1= new XElement(" ...
- 【人工智能】从零开始学好人工智能,AI知识体系和框架
写在前面: 最近公司的业务方向开始向AI方向改变(人工智能+文娱),但是现阶段AI方面的知识还没有储备,所以作为测试,也开始学习这方面的知识,不掉队. 知识储备: 1.阶段一-高等数学 高 ...
- 网易云和QQ音乐api
最近有点闲,听歌的时候遇见好听的想下载却遇到尴尬的事,版权!唉,知道我干什么了吧 网易云音乐 获取排行榜中的歌曲列表 https://music.163.com/discover/toplist?id ...
- 使用URLSearchParams处理axios发送的数据
使用URLSearchParams处理axios发送的数据 在使用axios这个ajax插件的时候,我们有些时候会遇到一些问题,比如:数据格式不正确 以最简单的例子为基础(这里使用post方法): 在 ...
- SQLserver登陆报错
https://blog.csdn.net/captain618/article/details/52331372 今天也不知道sql server抽了什么风,无论是windows登录还是sa登录,登 ...
