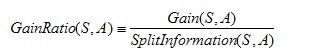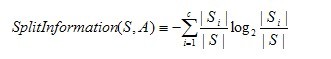决策树之ID3,C4.5及CART
决策树的基本认识
决策树学习是应用最广的归纳推理算法之一,是一种逼近离散值函数的方法,年,香农引入了信息熵,将其定义为离散随机事件出现的概率,一个系统越是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
假如一个随机变量 的取值为
的取值为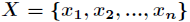 ,每一种取到的概率分别是
,每一种取到的概率分别是 ,那么
,那么
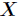 的熵定义为
的熵定义为
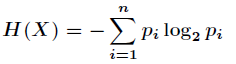
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
对于分类系统来说,类别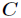 是变量,它的取值是
是变量,它的取值是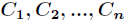 ,而每一个类别出现的概率分别是
,而每一个类别出现的概率分别是
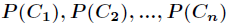
而这里的 就是类别的总数,此时分类系统的熵就可以表示为
就是类别的总数,此时分类系统的熵就可以表示为
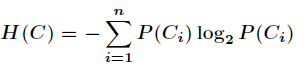
以上就是信息熵的定义,接下来介绍信息增益。
信息增益是针对一个一个特征而言的,就是看一个特征 ,系统有它和没有它时的信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即信息增益。
,系统有它和没有它时的信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即信息增益。
接下来以天气预报的例子来说明。下面是描述天气数据表,学习目标是play或者not play。
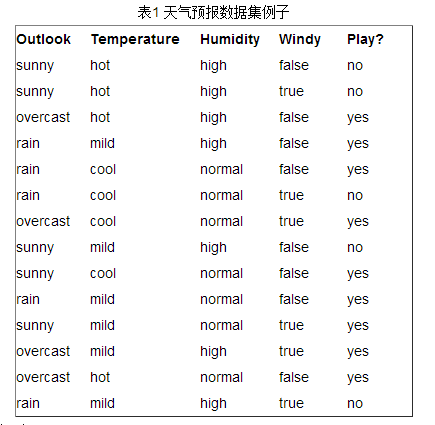
可以看出,一共14个样例,包括9个正例和5个负例。那么当前信息的熵计算如下

在决策树分类问题中,信息增益就是决策树在进行属性选择划分前和划分后信息的差值。假设利用
属性Outlook来分类,那么如下图
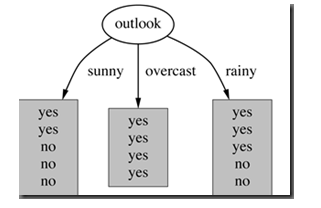
划分后,数据被分为三部分了,那么各个分支的信息熵计算如下

那么划分后的信息熵为
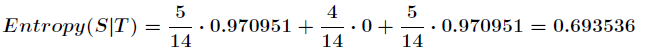
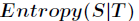 代表在特征属性
代表在特征属性 的条件下样本的条件熵。那么最终得到特征属性
的条件下样本的条件熵。那么最终得到特征属性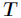 带来的信息增益为
带来的信息增益为
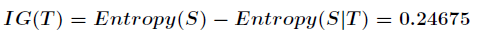
信息增益的计算公式如下
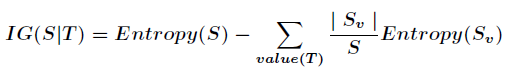
其中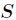 为全部样本集合,
为全部样本集合,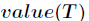 是属性
是属性 所有取值的集合,
所有取值的集合, 是
是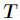 的其中一个属性值,
的其中一个属性值,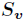 是
是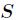 中属性
中属性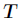 的值为
的值为 的样例集合,
的样例集合,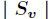 为
为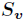 中所含样例数。
中所含样例数。
在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略。以上就是ID3算法的核心思想。
ID3的优缺点:
优点:
假设空间包含所有的决策树,它是关于现有属性的有限离散值函数的一个完整空间,避免搜索不完整假设空间的一个主要风险:假设空间可能不包含目标函数。
在搜索的每一步都使用当前的所有训练样例,不同于基于单独的训练样例递增作出决定,容错性增强。
在搜索过程中不进行回溯,可能收敛到局部最优而不是全局最优。
只能处理离散值的属性,不能处理连续值的属性。
信息增益度量存在一个内在偏置,它偏袒具有较多值的属性。
C4.5算法
C4.5 算法继承了ID3 算法的优点,并在以下几方面对ID3 算法进行了改进:
增益比率度量是用前面的增益度量Gain(S,A)和分裂信息度量SplitInformation(S,A)来共同定义的,如下所示:
其中,分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):
其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。
C4.5算法构造决策树的过程
- Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)
- Begin
- If S为空,返回一个值为Failure的单个节点;
- If S是由相同类别属性值的记录组成,
- 返回一个带有该值的单个节点;
- If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;
- [注意未出现错误则意味着是不适合分类的记录];
- For 所有的属性R(Ri) Do
- If 属性Ri为连续属性,则
- Begin
- 将Ri的最小值赋给A1:
- 将Rm的最大值赋给Am;
- For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m;
- 将Ri点的基于{< =Aj,>Aj}的最大信息增益属性(Ri,S)赋给A;
- End;
- 将R中属性之间具有最大信息增益的属性(D,S)赋给D;
- 将属性D的值赋给{dj/j=1,2...m};
- 将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};
- 返回一棵树,其根标记为D;树枝标记为d1,d2...dm;
- 再分别构造以下树:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
CART算法
使用基尼指数进行属性选择, 请参阅 https://blog.csdn.net/gzj_1101/article/details/78355234
决策树之ID3,C4.5及CART的更多相关文章
- 决策树模型 ID3/C4.5/CART算法比较
决策树模型在监督学习中非常常见,可用于分类(二分类.多分类)和回归.虽然将多棵弱决策树的Bagging.Random Forest.Boosting等tree ensembel 模型更为常见,但是“完 ...
- 机器学习算法总结(二)——决策树(ID3, C4.5, CART)
决策树是既可以作为分类算法,又可以作为回归算法,而且在经常被用作为集成算法中的基学习器.决策树是一种很古老的算法,也是很好理解的一种算法,构建决策树的过程本质上是一个递归的过程,采用if-then的规 ...
- ID3,C4.5和CART三种决策树的区别
ID3决策树优先选择信息增益大的属性来对样本进行划分,但是这样的分裂节点方法有一个很大的缺点,当一个属性可取值数目较多时,可能在这个属性对应值下的样本只有一个或者很少个,此时它的信息增益将很高,ID3 ...
- 决策树(ID3,C4.5,CART)原理以及实现
决策树 决策树是一种基本的分类和回归方法.决策树顾名思义,模型可以表示为树型结构,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布. [图片上传失败...(image ...
- 2. 决策树(Decision Tree)-ID3、C4.5、CART比较
1. 决策树(Decision Tree)-决策树原理 2. 决策树(Decision Tree)-ID3.C4.5.CART比较 1. 前言 上文决策树(Decision Tree)1-决策树原理介 ...
- ID3、C4.5、CART决策树介绍
决策树是一类常见的机器学习方法,它可以实现分类和回归任务.决策树同时也是随机森林的基本组成部分,后者是现今最强大的机器学习算法之一. 1. 简单了解决策树 举个例子,我们要对”这是好瓜吗?”这样的问题 ...
- 决策树(ID3、C4.5、CART)
ID3决策树 ID3决策树分类的根据是样本集分类前后的信息增益. 假设我们有一个样本集,里面每个样本都有自己的分类结果. 而信息熵可以理解为:“样本集中分类结果的平均不确定性”,俗称信息的纯度. 即熵 ...
- 决策树 ID3 C4.5 CART(未完)
1.决策树 :监督学习 决策树是一种依托决策而建立起来的一种树. 在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某 ...
- 决策树(上)-ID3、C4.5、CART
参考资料(要是对于本文的理解不够透彻,必须将以下博客认知阅读,方可全面了解决策树): 1.https://zhuanlan.zhihu.com/p/85731206 2.https://zhuanla ...
- 21.决策树(ID3/C4.5/CART)
总览 算法 功能 树结构 特征选择 连续值处理 缺失值处理 剪枝 ID3 分类 多叉树 信息增益 不支持 不支持 不支持 C4.5 分类 多叉树 信息增益比 支持 ...
随机推荐
- Mathematica求微分换元
[转载请注明出处]http://www.cnblogs.com/mashiqi 2017/12/16 有时我们需要对PDEs中的各项进行变量替换,比如把$\frac{\text{d}}{\text{d ...
- XAF创建一个DashBoard
1.首先启动windows程序之后点击DashBoard导航栏 2.接着点击新建按钮,开始创建一个DashBoard 3.接着根据你的数据来源选择数据源,这里我选择了数据库 4.接着填好你的服务器和数 ...
- log4net使用中loginfo.IsInfoEnabled=false问题解决方法
引用了其他项目中的日志组件,调试时发现IsInfoEnabled属性一直为false 找了很多的解决办法,都不行 program.cs里面也不用添加 log4net.Config.XmlConfigu ...
- 关于使用deepin在linux下安装mysql出现Can't connect to local MySQL server through socket '/tmp/mysql/mysql.sock' (2)的解决方法
根据目录/etc/mysql打开文件debain.cnf 此时文本里的内容为 # Automatically generated for Debian scripts. DO NOT TOUCH