前端bug记录

记录一下前端入门时期遇到的一些bug。

1、同步、异步问题

背景：Javascript语言的执行环境是单线程。即一次只能完成一个任务。若有多个任务则需排队逐个执行——前一个任务完成，再执行后一个任务。

JS语言将任务执行模式分为异步和同步。

同步模式就是上一段的模式，后一个任务等待前一个任务结束，然后再执行，程序的执行顺序与任务的排列顺序是一致的、同步的；

异步模式则完全不同，每一个任务有一个或多个回调函数（callback），前一个任务结束后，不是执行后一个任务，而是执行回调函数，后一个任务则是不等前一个任务结束就执行，所以程序的执行顺序与任务的排列顺序是不一致的、异步的。

解决方案：
①使用async + await

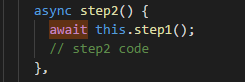
例如：step2函数再被调用时，会先等待step1函数执行完毕后再进行step2 code。

②nextTick

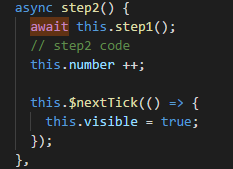
例如：在执行step2函数时，number++计算完毕后，才会调用nextTick中的显示visible。

③回调函数

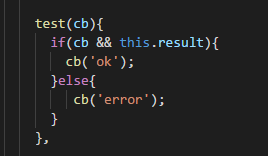
例如： test函数中调用了回调函数cb，如果结果正确则回调函数返回‘ok’，否则返回‘error’；

那么我们再调用test函数时会对回调函数进行定义：

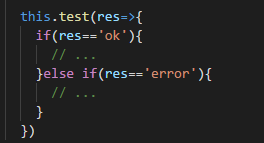
2、Vue 记录 Cannot read property '_withTask' of undefined
描述：使用的事件或数据无效（未定义）

解决方案：一个个排查事件和数据是否定义，养成习惯先定义数据和事件再调用。

3、Object的值未改变

背景：修改obj的值时候，页面未渲染。
解决方案：使用this.$set(obj,key,newvalue)替代直接对对象的赋值。