octave基本操作

参考： https://blog.csdn.net/iszhenyu/article/details/78712228；  吴恩达机器学习视频；

在学习机器学习的过程中，免不了要跟MATLAB、Octave打交道，这两个工具都可以帮助我们很好的解决数值计算问题，两者的语法也非常接近。

Octave是一个完全开源免费的软件，无论是Windows还是Mac环境都可以在官网下载安装包直接安装，非常方便。

这篇文章主要介绍在学习机器学习的过程中会经常使用到的Octave的一些命令和语法。当然，一篇文章肯定无法覆盖Octave的所有功能，但是对于我们入门机器学习应该足够了。

基本计算

Octave中的 加、减、乘、除运算：

>> 2 + 2
ans =  4
>> 3 - 2
ans =  1
>> 5 * 8
ans =  40
>> 1 / 2
ans =  0.50000

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

同时也可以进行平方、立方等指数运算：

>> 2^2
ans =  4
>> 2^3
ans =  8

• 1
• 2
• 3
• 4

在Octave中，我们可以使用符号 % 来进行注解，其后面的同行语句都将不会得到执行。例如：2 + 3 % + 5 输出的结果为5。如果你熟悉java语言，可以类比为//，或者是Python中的#。

逻辑运算

常用的逻辑运算包括：等于（==）、不等于（~=）、并（&&）、或（||）四种，分别用不同的符号表示。

运算的结果用0、1表示，1表示成立，0表示不成立。

>> 1 == 2
ans = 0
>> 1 == 1
ans =  1
>> 1 ~= 2
ans =  1
>> 1 && 0
ans = 0
>> 1 || 0
ans =  1

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

在Octave中，同时还内置了一些函数来进行逻辑运算，比如异或运算就可以用xor这个函数来代替：

>> xor(3, 1)
ans = 0
>> xor(3, 3)
ans = 0
>> xor(1, 0)
ans = 1

• 1
• 2
• 3
• 4
• 5
• 6

在Octave中内置了很多的函数，有时，我们可能记不太清某个函数的具体用法，这个时候，Octave给我们提供了 help 命令，通过这个命令可以查看函数的定义以及示例。比如，我们想看下xor这个函数怎么用，可以输入：help xor。

变量

同其他编程语言一样，我们也可以在Octave中定义变量，语法跟其他语言也比较类似：

>> a = 3
a =  3
>> a = 3;
>>

• 1
• 2
• 3
• 4

上面的例子中，我们定义了变量a，并将它赋值为3。

有一个细节需要我们注意的是：在第一次执行a = 3的后面没有加;号，Octave在执行完赋值语句后又打印出了变量a的值。而在第二句中，我们在赋值语句的末尾添加了;号，这个时候，Octave只会执行赋值语句，将不再打印变量值。

除了将数值赋给一个变量，我们也可以将字符串、常量赋给变量：

>> b = 'hi'; % 因为加了;号，没有打印出b的值
>> b         % 直接输入变量名称，即可打印变量值
b = hi

>> c = (3 >= 1)
c =  1

>> a = pi;
>> a
a =  3.1416

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

在上面的第二行语句，直接输入了变量名称（没有分号），Octave直接打印出了变量的值。

除此以外，也可以使用disp函数来完成打印变量值的功能：

>> disp(a)
 3.1416

• 1
• 2

结合printf函数，还能实现格式化打印。还是以上面的变量a为例：

>> disp(sprintf('2 decimals: %0.2f', a))
2 decimals: 3.14

>> disp(sprintf('6 decimals: %0.6f', a))
6 decimals: 3.141593

• 1
• 2
• 3
• 4
• 5

printf 函数沿用了C语言的语法格式，所以如果你有学习过C语言的话，对上面的写法应该会比较熟悉。

除了使用printf外，利用format long、format short也可以指定打印的精度，在Octave中，short是默认的精度：

octave:32> format long
octave:33> a
a =  3.14159265358979

octave:34> format short
octave:35> a
a =  3.1416

• 1
• 2
• 3
• 4
• 5
• 6
• 7

向量和矩阵

向量/矩阵的生成

在Octave中可以这样定义矩阵：将矩阵的元素按行依次排列，并用[]包裹，矩阵的每一行用;分割。

下面定义了一个3×2的矩阵A

>> A = [1 2; 3 4; 5 6]
A =
   1   2
   3   4
   5   6

• 1
• 2
• 3
• 4
• 5

说明：; 号在这里的作用可以看做是换行符，也就是生成矩阵的下一行。

在命令行下，也可以将矩阵的每一行分开来写：

>> A = [1 2;
> 3 4;
> 5 6]
A =
   1   2
   3   4
   5   6

• 1
• 2
• 3
• 4
• 5
• 6
• 7

向量的创建与矩阵类似：

>> V1 = [1 2 3]
V1 =
   1   2   3

>> V2 = [1; 2; 3]
V2 =
   1
   2
   3

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

在上面的例子中，V1是一个行向量，V2是一个列向量。

其他一些写法：

>> V = 1: 0.2: 2
V =
    1.0000    1.2000    1.4000    1.6000    1.8000    2.0000

• 1
• 2
• 3

上面的写法可以快速生成行向量，1 为起始值，0.2为每次递增值，2为结束值，我们也可以省略0.2，那么就会生成递增为1的行向量：

>> v = 1:5
v =
   1   2   3   4   5

• 1
• 2
• 3

同样，我们也可以利用Octave内置的函数来生成矩阵，比较常用的几个函数是ones、zeros、rand、eye。

ones(m, n) 函数生成一个m行n列的矩阵，矩阵中每个元的值为1。

zeros(m, n) 函数生成一个m行n列的矩阵，矩阵中每个元的值为0。

rand(m, n) 函数生成一个m行n列的矩阵，矩阵的每个元是0到1之间的一个随机数。

eye(m) 函数生成一个大小为m的单位矩阵。

>> ones(2, 3)
ans =
   1   1   1
   1   1   1

>> w = zeros(1, 3)
w =
   0   0   0

>> w = rand(1, 3)
w =
   0.19402   0.23458   0.49843

>> eye(4)
ans =
Diagonal Matrix
   1   0   0   0
   0   1   0   0
   0   0   1   0
   0   0   0   1

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20

向量/矩阵的属性

在说明矩阵的属性操作之前，我们先来定义一个矩阵A：

>> A
A =
   1   2
   3   4
   5   6

• 1
• 2
• 3
• 4
• 5

矩阵有了，怎么知道一个矩阵的大小呢？在Octave中，内置了size函数。

size函数返回的结果也是一个矩阵，但这个矩阵的大小是1×2，这个1×2的矩阵中，两个元素的值分别代表了参数矩阵的行数和列数。

>> sa = size(A);
>> sa
sa =
   3   2

>> size(sa)
ans =
   1   2

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

当然，我们也可以只获取矩阵的行数或列数，使用的同样是size函数，唯一不同的是需要多指定一个参数，来标识想获取的是行还是列，这个标识用1或2来表示，1代表想获取的是行数，2代表想获取的是列数：

>> size(A, 1)
ans =  3
>> size(A, 2)
ans =  2

• 1
• 2
• 3
• 4

除了size函数，另外一个比较常用的是length函数，它获取的是矩阵中最大的那个维度的值，也就是说，对于一个m×n的矩阵，return m if m > n else n。

对于向量来说，利用length可以快速获取向量的维数：

>> V = [1 2 3 4]
V =
   1   2   3   4

>> length(V)
ans =  4

octave:67> length(A)
ans =  3

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

向量/矩阵的运算

我们还是以上一小节定义的矩阵A为例。

获取矩阵指定行指定列的元素，注意这里的行、列都是从1开始的，比如获取矩阵A的第3行第2列元素：

>> A(3, 2)
ans =  6

• 1
• 2

也可以获取矩阵整行或整列的元素，某行或某列的全部元素可以用 : 号代替，返回的结果就是一个行向量或一个列向量：

>> A(3,:)
ans =
   5   6

>> A(:, 2)
ans =
   2
   4
   6

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

更一般情况，我们也可以指定要获取的某几行或某几列的元素：

>> A([1, 3],:)
ans =
   1   2
   5   6

>> A(:,[2])
ans =
   2
   4
   6

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

除了获取矩阵元素，我们也可以给矩阵的元素重新赋值。可以给指定行指定列的某一个元素赋值，也可以同时给某行或某列的全部元素一次性赋值：

>> A(:,2) = [10, 11, 12]
A =
    1   10
    3   11
    5   12

>> A(1,:) = [11 22]
A =

   11   22
    3    4
    5    6

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12

有的时候，我们还需要对矩阵进行扩展，比如增广矩阵，要在矩阵的右侧附上一个列向量：

>> A = [A, [100; 101; 102]]
A =
     1    2   100
     3    4   101
     5    6   102

• 1
• 2
• 3
• 4
• 5

上面第一句中，, 号也可以省略，只使用空格也是一样的效果。这样，那行赋值语句就变成这样：A = [A [100; 101; 102]]

两个矩阵也可以进行组合：

>> A = [1 2; 3 4; 5 6]
A =
   1   2
   3   4
   5   6

>> B = [11 12; 13 14; 15 16]
B =
   11   12
   13   14
   15   16

>> [A B]
ans =
    1    2   11   12
    3    4   13   14
    5    6   15   16

>> [A; B]
ans =
    1    2
    3    4
    5    6
   11   12
   13   14
   15   16

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26

我们也可以将矩阵的每一列组合在一起，转为一个更大的列向量：

>> A(:)
ans =
     1
     3
     5
     2
     4
     6

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

接下来，为了说明矩阵与矩阵的运算，我们先来定义三个矩阵：

>> A
A =
   1   2
   3   4
   5   6

>> B
B =
   11   12
   13   14
   15   16

>> C
C =
   1   1
   2   2

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

矩阵的相乘：

>> A*C
ans =
    5    5
   11   11
   17   17

• 1
• 2
• 3
• 4
• 5

矩阵A的各个元素分别乘以矩阵B对应元素：

>> A .* B
ans =
   11   24
   39   56
   75   96

• 1
• 2
• 3
• 4
• 5

点运算在这里可以理解为是对矩阵中每个元素做运算。比如，下面的例子就是对A中每个元素做平方，用1分别去除矩阵中的每个元素：

>> A .^ 2
ans =
    1    4
    9   16
   25   36

>> 1 ./ [1; 2; 3]
ans =
   1.00000
   0.50000
   0.33333

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

有一种特殊情况是，当一个实数与矩阵做乘法运算时，我们可以省略.直接使用*即可：

>> -1 * [1; -2; 3]  % 也可以简写为 -1[1; 2; 3]
ans =
  -1
   2
  -3

• 1
• 2
• 3
• 4
• 5

除此以外，Octave中内置的一些函数也是针对每个元素做运算的，比如对数运算、指数运算和绝对值运算等：

octave:50> log([1; 2; 3])
ans =
   0.00000
   0.69315
   1.09861

octave:51> exp([1; 2; 3])
ans =
    2.7183
    7.3891
   20.0855

octave:53> abs([1; -2; 3])
ans =
   1
   2
   3

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17

矩阵的加法、转秩和逆：

>> V + ones(length(V), 1)  % V = [1; 2; 3]
ans =
   2
   3
   4

% 矩阵的转秩
>> A'
ans =
   1   3   5
   2   4   6

% 求矩阵的逆
>> pinv(A)
ans =
   0.147222  -0.144444   0.063889
  -0.061111   0.022222   0.105556
  -0.019444   0.188889  -0.102778

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18

其他一些运算：

% a = [1 15 2 0.5]，求最大值
>> val = max(a)
val =  15

% 求最大值，并返回最大值的索引
>> [val, idx] = max(a)
val =  15
idx =  2

% 矩阵对应元素的逻辑运算
>> a <= 1
ans =
   1   0   0   1

>> find(a < 3)
ans =
   1   3   4

% 计算之和
>> sum(a)
ans =  18.500

% 计算乘积
>> prod(a)
ans =  15

% 向下取整
>> floor(a)
ans =
    1   15    2    0

% 向上取整
>> ceil(a)
ans =
    1   15    2    1

% 生成一个随机矩阵，矩阵元素的值位于0-1之间
>> rand(3)
ans =
   0.458095   0.323431   0.648822
   0.481643   0.789336   0.559604
   0.078219   0.710996   0.797278

% 矩阵按行上下对换
>> flipud(eye(4))
ans =
Permutation Matrix

   0   0   0   1
   0   0   1   0
   0   1   0   0
   1   0   0   0

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52

控制语句和函数

for、while、if 语句

octave中for，while,if语句的使用方式和c语言一样，不同的是大括号的功能是通过end实现的，下面例子中空格没有任何作用，只是起到视觉上清晰的作用。

首先我们定义一个列向量：V = zeros(10, 1)，然后通过 for 循环语句来更新向量V中的每一个元素：

>> for i=1:10,
       V(i) = 2^i;
   end;
>> V
V =
      2
      4
      8
     16
     32
     64
    128
    256
    512
   1024

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

或者，我们也可以换一种写法：

>> indices = 1:10;
>> indices
indices =
    1    2    3    4    5    6    7    8    9   10

>> for i=indices,
       disp(i);
   end;
 1
 2
 3
 4
 5
 6
 7
 8
 9
 10

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18

每一个 for 循环都是用 end 来结尾，固定写法，记住就好。

下面看while语句：

>> i = 1;
>> while i <= 5,
        disp(V(i));
        i = i+1;
   end;
 2
 4
 8
 16
 32

>> i = 1;
>> while true,
        disp(V(i));
        if i > 5,
            break;
        end;
        i = i + 1;
   end;
 2
 4
 8
 16
 32
 64

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25

while 和 if 语句同样需要使用 end 来表示完结，同时，在 for 或 while 中，我们也可以使用 break 关键词来提前退出循环。

函数

我们还是先看例子，然后再说明具体的写法：

>> function y = squareNum(x)
       y = x^2;
   end;
>> squareNum(3)
ans =  9

• 1
• 2
• 3
• 4
• 5

在Octave中，定义一个函数需要使用function 关键字，然后紧跟在 function 后面的是函数的声明，包括返回值，函数名称和参数，之后换行来实现具体的函数功能。

Octave的函数不需要显示的返回语句，Octave会将函数第一行声明的返回值返回给调用方，因此，我们在函数体中只需将最终的计算结果赋给定义的返回值，比如上面例子中的y。

还有一点需要说明的是，在Octave中，函数可以返回多个值：

>> function [y1, y2] = calVal(x)
       y1 = x^2;
       y2 = x^3;
   end;
>> [a, b] = calVal(3)
a =  9
b =  27

• 1
• 2
• 3
• 4
• 5
• 6
• 7

也可以把函数写进文件中，然后加载实现函数。

进入octave后，cd到指定的目录下，这里我是把函数文件存在d盘下的文件中

cd D:\app2018\octave

之后你可以用pwd打印出当前目录的路径看看是否是在该文件下。

在该目录下新建一个文件名为“squareThisNumber.m”后缀是.m这样octave可以自动识别，双击后就会用notepad++自动打开，就可以编辑自己的函数。

注意：文件名要和函数名保持一致。

function y = squareThisNumber(x)
y = x^2;

函数的返回值是y，函数的自变量是x（这里只有一个返回值，可以有多个返回值），函数的主体是y = x^2

>squareThisNumber(5)

ans = 25

这样就实现一简单求数平方的函数。

加载和保存数据

在上面一节中，介绍了如何在Octave的交互环境定义函数。但是大部分时候，我们都会将函数保存在文件中，从而在需要时可以随时调用。我们也能够在文件中存储数据，比如矩阵参数等，使用 load 命令可以将文件中的内容加载进来。

通常会比较常用的一些命令有如下几个：

显示当前的工作目录：

>> pwd
ans = /Users/xiaoz

• 1
• 2

进到指定的目录：

>> cd octave
>> pwd
ans = /Users/xiaoz/octave

• 1
• 2
• 3

列出当前目录下的文件：

>> ls
featureX.dat    priceY.dat

• 1
• 2

加载当前目录下的数据（也可以使用load函数）：

>> load featuresX.dat
>> load pricesY.dat

• 1
• 2

查看当前工作空间下都有哪些变量：

>> who
Variables in the current scope:
ans  featuresX  pricesY

• 1
• 2
• 3

查看详细的变量信息：

>> whos
Variables in the current scope:

   Attr Name           Size                     Bytes  Class
   ==== ====           ====                     =====  =====
        ans            1x13                        13  char
        featuresX      3x2                         48  double
        pricesY        3x1                         24  double

Total is 22 elements using 85 bytes

>> featuresX  % 查看加载进来的变量
featuresX =
   123     1
   456     2
   789     3

octave:15> pricesY
pricesY =
   11
   22
   33

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22

clear 命令可以清除一个变量，需要特别小心的是，如果后面没有跟具体的变量名，则会清空全部变量：

>> clear ans

• 1

保存数据到指定的文件，它的语法格式是这样的：

save {file_name} {variables}

>> V = pricesY(1:2)  % 获取第一列的前两个元素
V =
   11
   22

% 保存变量V到hello.mat文件
>> save hello.mat V;

>> ls
featuresX.dat   hello.mat   pricesY.dat

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

在保存的时候也可以指定一种编码格式，比如下面的例子指定了 ascii 编码，如果不指定，数据将会被保存为二进制格式。

>> save hello.txt V -ascii

• 1

有一点需要提示的是：假如你使用pwd命令发现当前的工作目录是A，同时你实现了一个函数someFunc，存储在文件someFunc.m中，如果这个someFunc.m文件不在A目录，那么在使用someFunc函数之前，需要先调用load方法将其加载进来，反之可以直接使用。

绘制图形

在本篇文章的最后一节，我们来简单的说下Octave的绘图能力。

不像其他语言那般繁琐，Octave中绘图的接口设计的非常简洁和直观，让你非常容易上手。

我们以绘制一个sin函数曲线和一个cos函数曲线为例，来说明如何在Octave中绘图。

首先，我们还是先来定义数据

>> t = [0:0.01:0.98];
>> y1 = sin(2*pi*4*t);
>> y2 = cos(2*pi*4*t);

• 1
• 2
• 3

这里的t我们看做是横轴，y1看做是纵轴，然后调用plot函数

>> plot(t, y1);

• 1

之后会立即在一个新窗口生成我们想要的图形

接下来我们继续在这个图像上绘制cos函数。这时需要用到hold on命令，它的作用是将新图像画在旧图像上面，而不是覆盖旧图像。

为了区分sin函数，我们将cos函数的曲线用红色标识：

octave:10> hold on;
octave:11> plot(t,y2, 'r');

• 1
• 2

这个时候，你看到的图形应该是这个样子的：

图形有了，最后一步就是标明横轴和纵轴分别代表的含义，再给图形起一个有意义的名字

>> xlabel('time');   % 指定X轴的名称
>> ylabel('value');  % 指定Y轴的名称
>> legend('sin', 'cos');  % 标识第一条曲线是sin，第二条曲线是cos
>> title('sin and cos function');   % 给图片附一个标题

• 1
• 2
• 3
• 4

最终，这个图形是这样式的：

如果你愿意，还可以将其作为一个图片保存下来：

octave:16> print -dpng 'sin_cos.png'

• 1

在绘图中，如果你反悔了，想重新绘图，怎么办呢？也很简单，只要输入clf命令，Octave会将绘图框中的图形全部清空。

不论何时，输入close命令，Octave会关闭该绘图窗口。

>figure(1);plot(t,y1);

>figure(2);plot(t,y2);

这样就可以分别用两个窗口显示图像。

>subplot(1,2,1);   %这样做是把窗口分成一个1*2的格子，使用第一个格子；

>plot(t,y1);

>subplot(1,2,2);

>plot(t,y2);

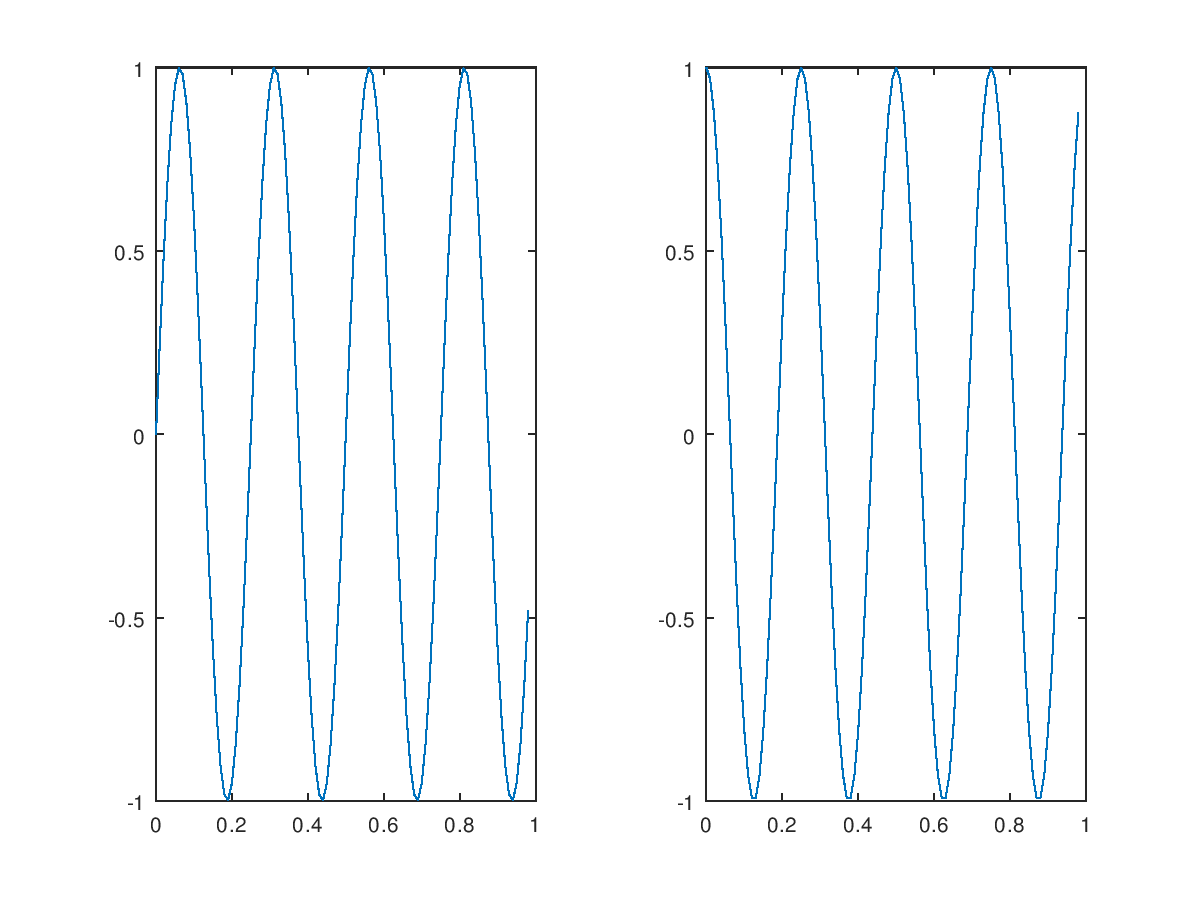
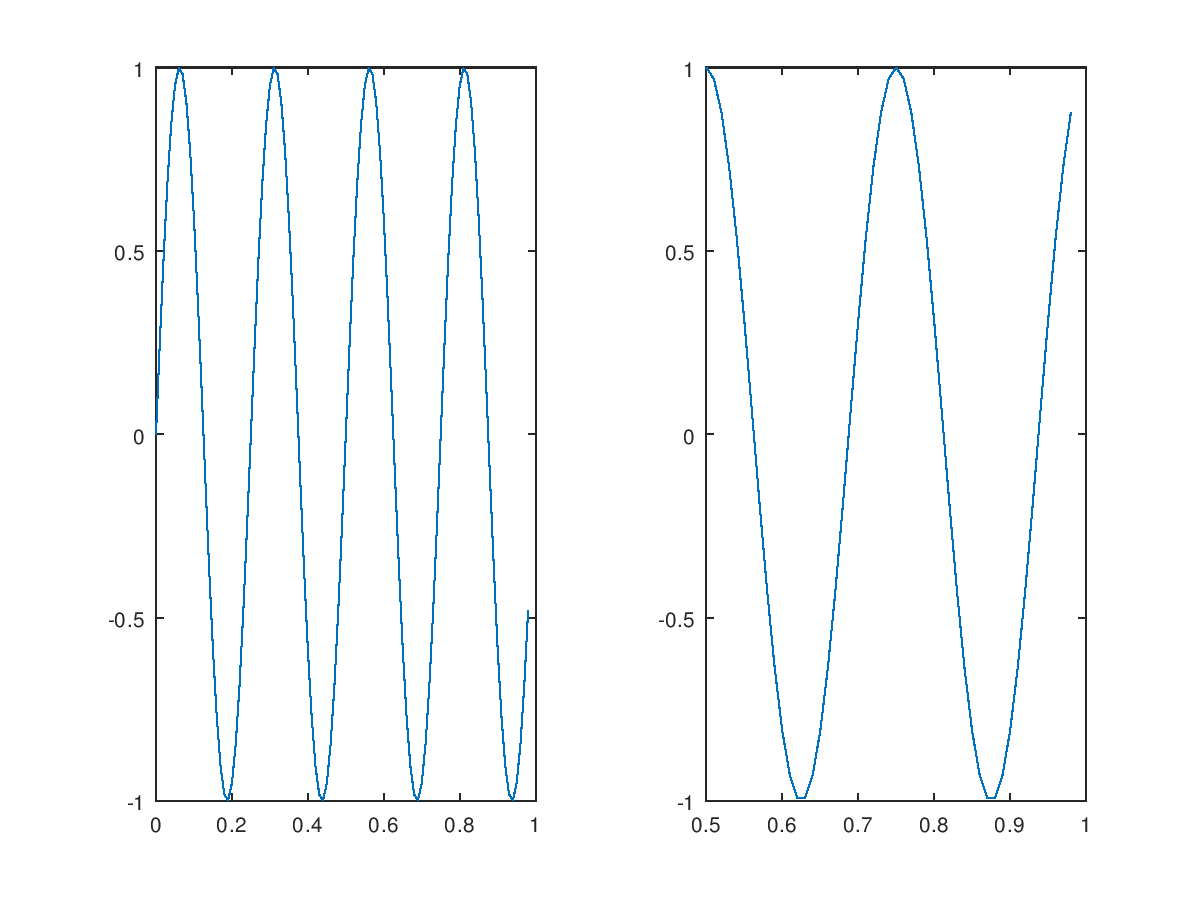
axis(0.5 1 -1 1)  %调整右边图像的x，y坐标的范围。

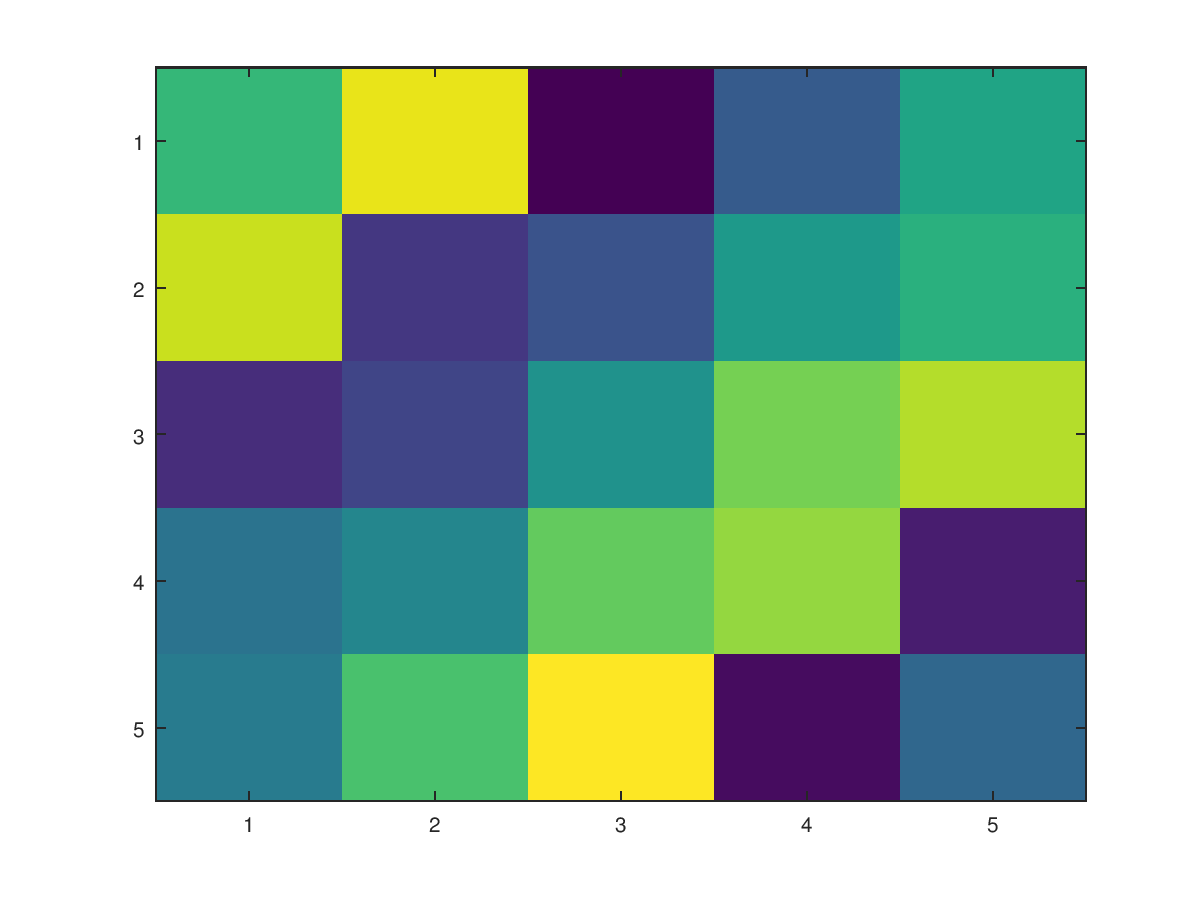
>A = magic(5);

>imagesc(A); %生成一个5*5 的色块

矢量

有道时候方程向量化，计算起来会更加高效。

A = [a1;a2;a3;........;an]

X = [x1;x2;x3;..........xn]

例子：h(x) = a1x1 + a2x2 + a3x3 + .........+ anxn = AX'(X的转置);

没有向量化之前可能会使用for循环的方式实现求和函数，但是转换成向量来做只需要一条语句就能实现；

p = A * X‘ ；

其实，Octave能做的远远不止这些，本篇介绍的这些也不过是冰山一角，但对于我们实践机器学习的算法已经基本足够。不要忘记的是，当你对某个函数不清楚的时候，试试help {func name}。