（线性dp，最大连续和）Max Sequence

Max Sequence

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 18511		Accepted: 7743

Description

Give you N integers a1, a2 ... aN (|ai| <=1000, 1 <= i <= N). 

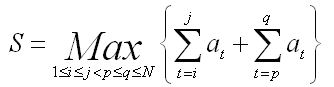
You should output S. 

Input

The input will consist of several test cases. For each test case, one integer N (2 <= N <= 100000) is given in the first line. Second line contains N integers. The input is terminated by a single line with N = 0.

Output

For each test of the input, print a line containing S.

Sample Input

5
-5 9 -5 11 20
0

Sample Output

40

最大连续和问题的升级版，先从左边遍历一次，从右边遍历一次，分成两部分，然后相加，最后取最大值。   最大连续和的状态转换式为：dp[i] = max(dp[i-1]+a[i],a[i])
可以打表，注意两次遍历时的初始化情况，还有得用m1和m2数组保存前i个数的最大连续和和后j个数的最大连续和。这样接下来就可以用m1[i] + m2[i+1]的最大值作为答案。
C++代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn = ;
int a[maxn],dpl[maxn],dpr[maxn],m1[maxn],m2[maxn];
int Inf = -0x3f3f3f3f;
int main(){
    int n;
    while(~scanf("%d",&n)){
        if(n==)
            break;
        for(int i = ; i <= n; i++){
            scanf("%d",&a[i]);
        }
        memset(dpl,,sizeof(dpl));
        memset(dpr,,sizeof(dpr));
        m1[] = m2[n+] = Inf;
        for(int i = ; i <= n; i++){
            dpl[i] = max(dpl[i-] + a[i],a[i]);
            if(m1[i-] < dpl[i])
                m1[i] = dpl[i];
            else
                m1[i] = m1[i-];
        }
        for(int i = n; i >= ; i--){
            dpr[i] = max(dpr[i+] + a[i],a[i]);
            if(m2[i+] < dpr[i])
                m2[i] = dpr[i];
            else
                m2[i] = m2[i+];
        }
        int maxsum = Inf;
        int tmp[maxn];
        for(int i = ; i <= n-; i++){
            tmp[i] = m1[i] + m2[i+];
            if(maxsum < tmp[i])
                maxsum = tmp[i];
        }
        printf("%d\n",maxsum);
    }
    return ;
}